Файл: Контрольная работа за 2 семестр По дисциплине Математика Вариант 2 Фамилия Имя.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 30
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Решение.
Сначала найдем общее решение однородного уравнения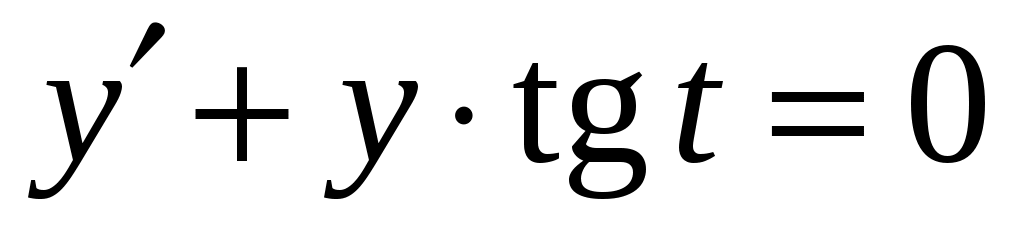 . Разделим переменные
. Разделим переменные 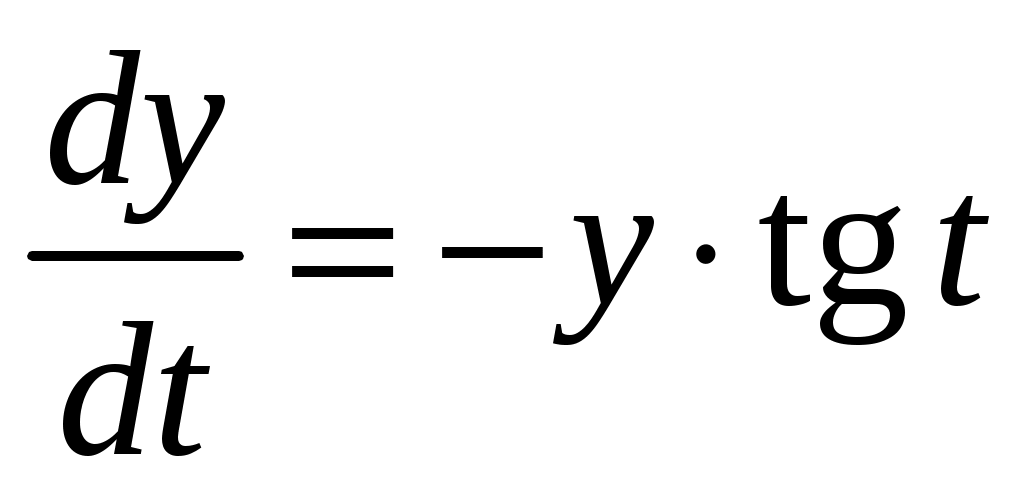 ,
, 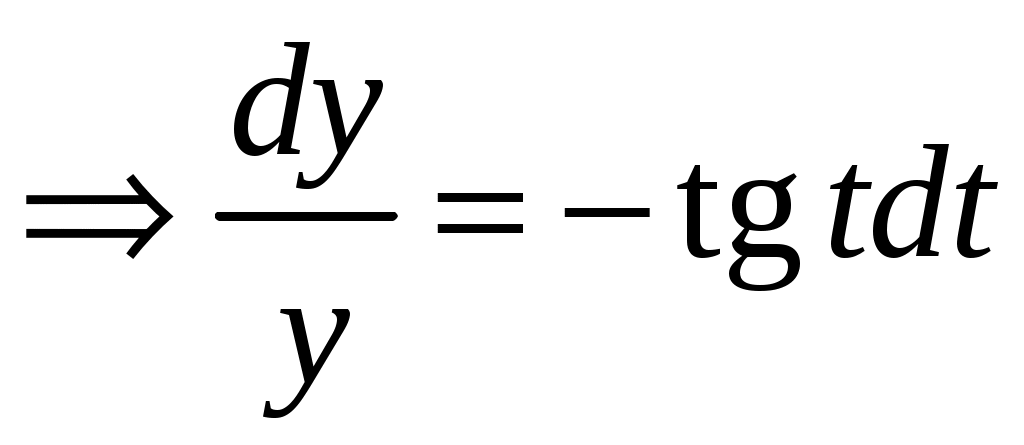 . Интегрируем левую и правую части
. Интегрируем левую и правую части 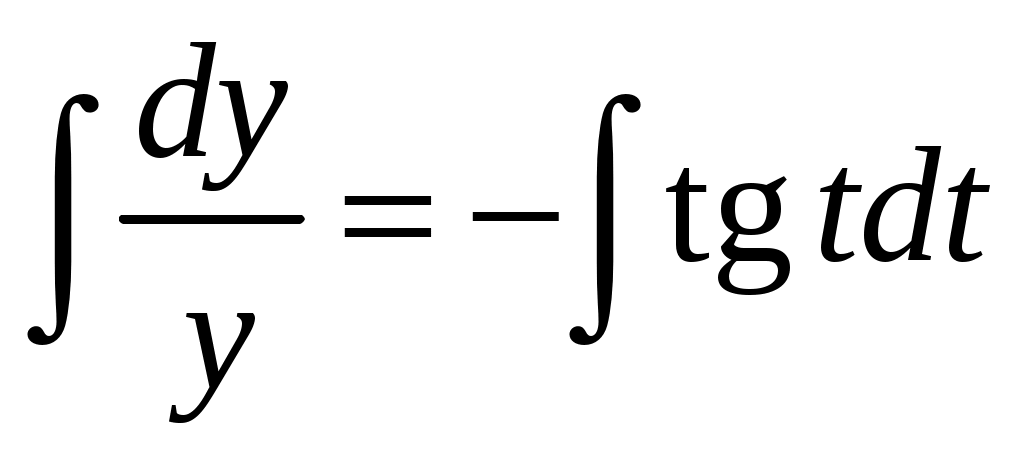 , получим
, получим 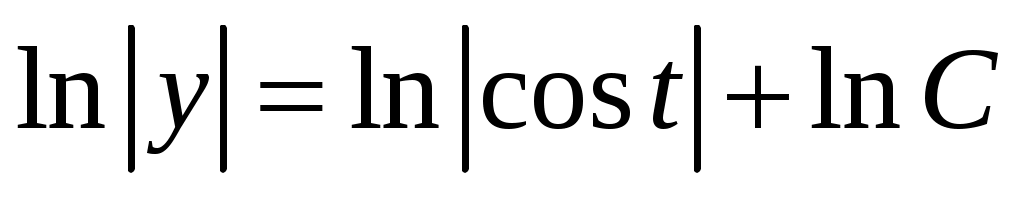 ,
, 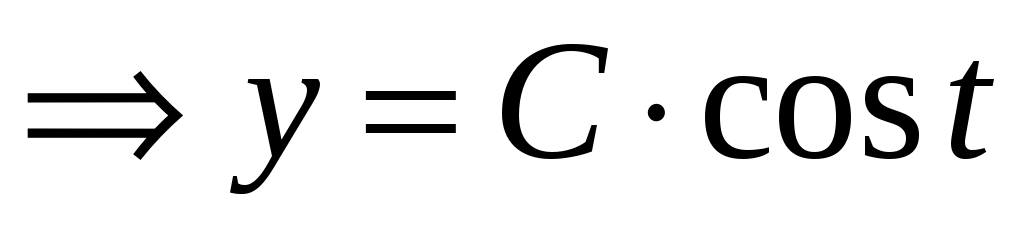 .
.
Общее решение исходного уравнения будем искать в виде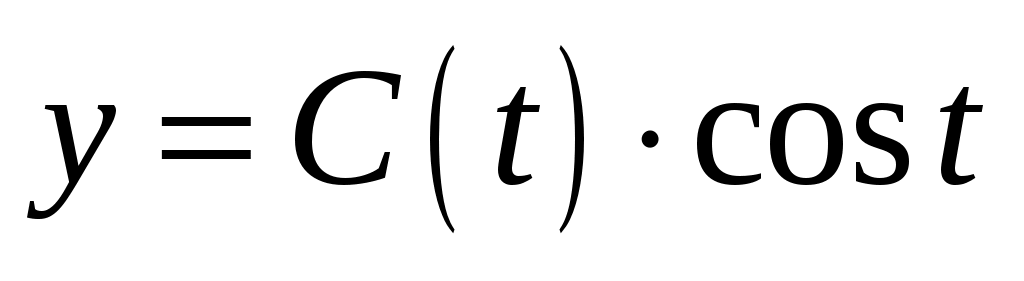 . Дифференцируем
. Дифференцируем 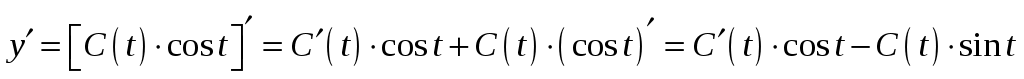 . Выражения для
. Выражения для  и
и 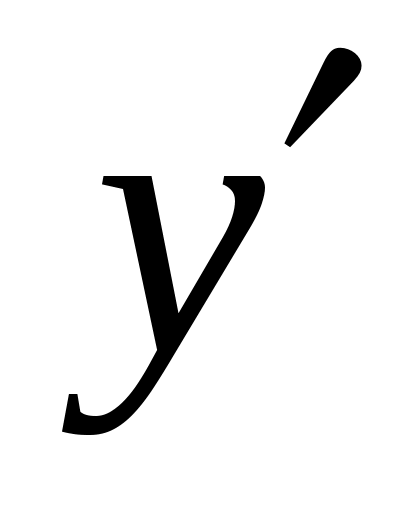 подставим в исходное уравнение, получим:
подставим в исходное уравнение, получим:
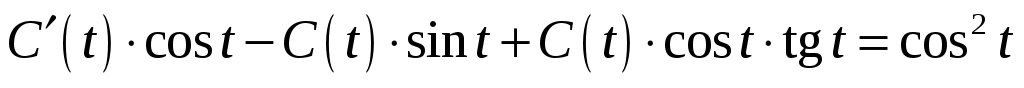 ;
;
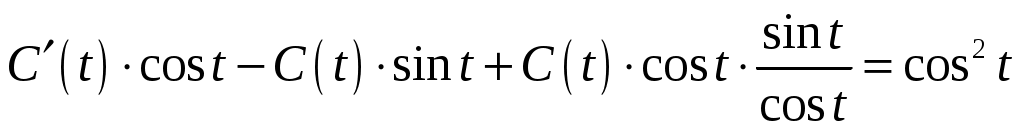 ;
;
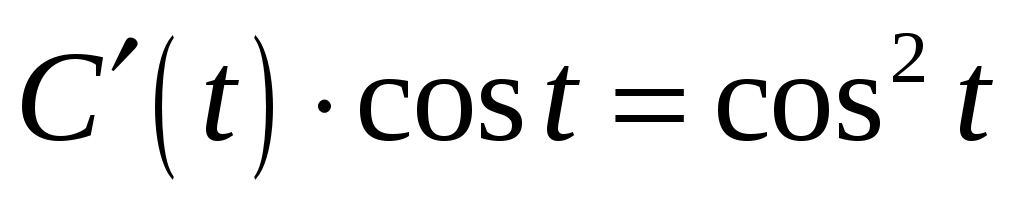 ,
, 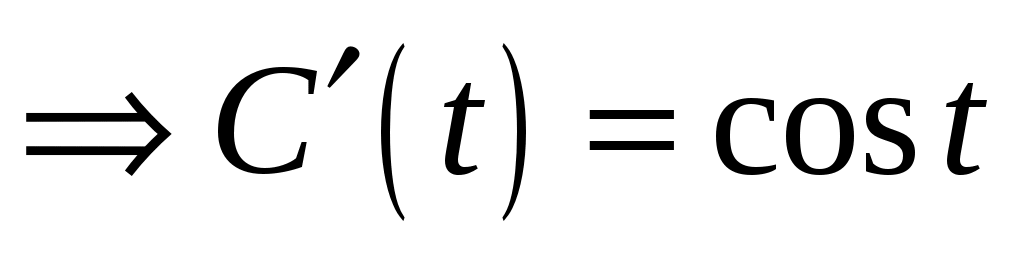
Интегрируем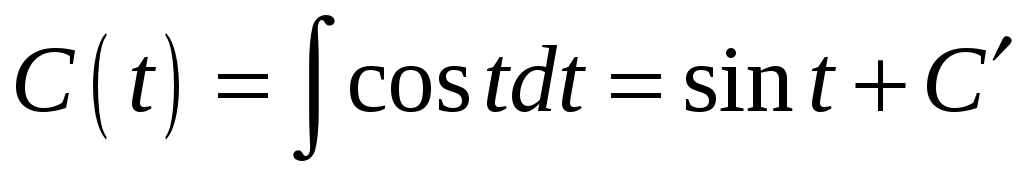 . Общее решение исходного уравнения равно
. Общее решение исходного уравнения равно 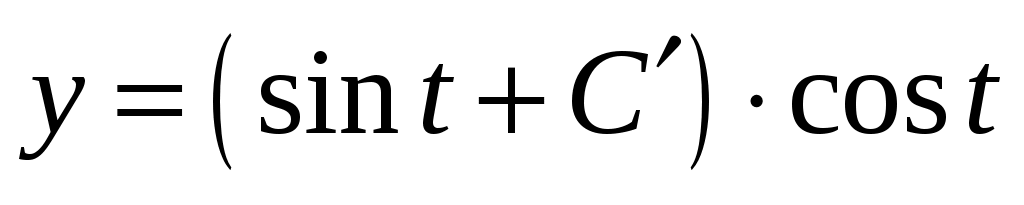 .
.
Найдем частное решение, удовлетворяющее начальному условию , получим
, получим 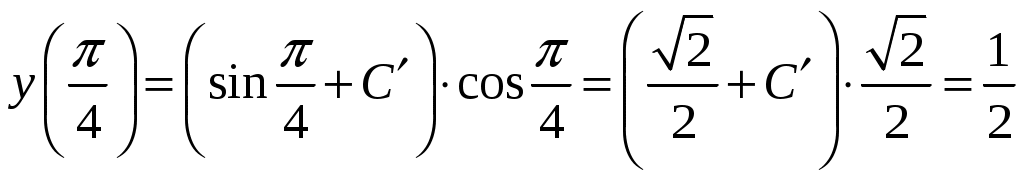 ,
, 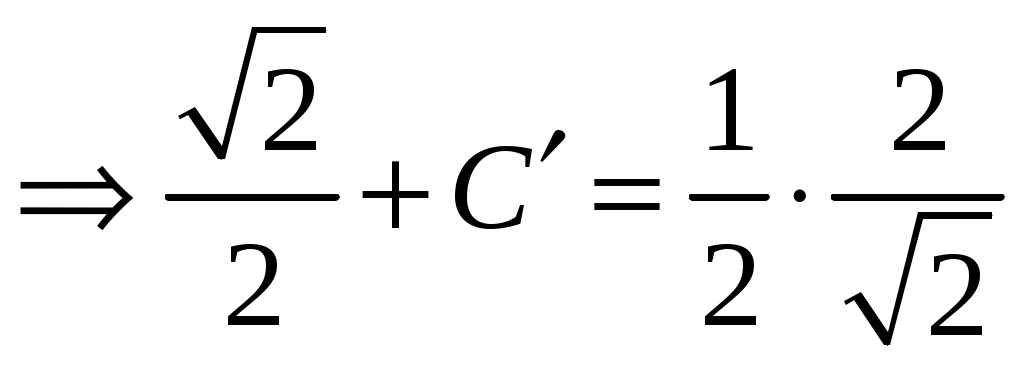 ,
, 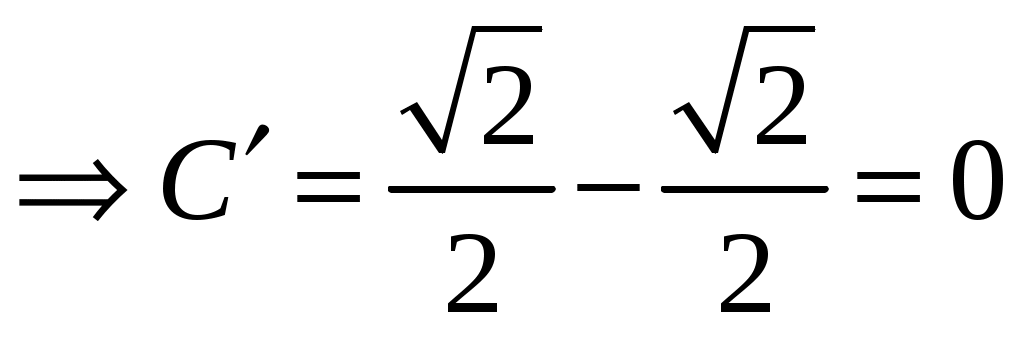 .
.
Частное решение равно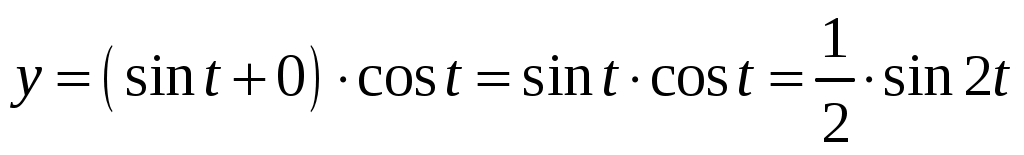 .
.
Ответ: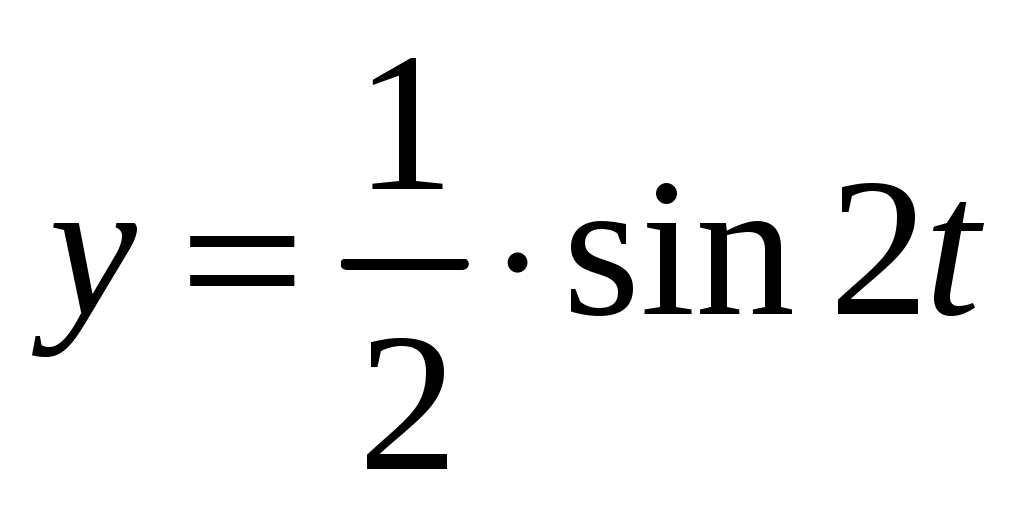 .
.
Задача 42. Найти частное решение линейного однородного ДУ второго порядка.
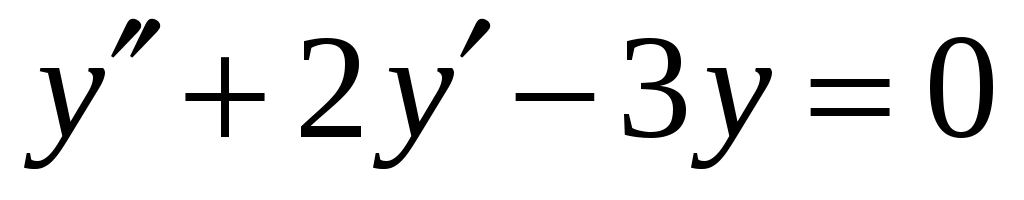
,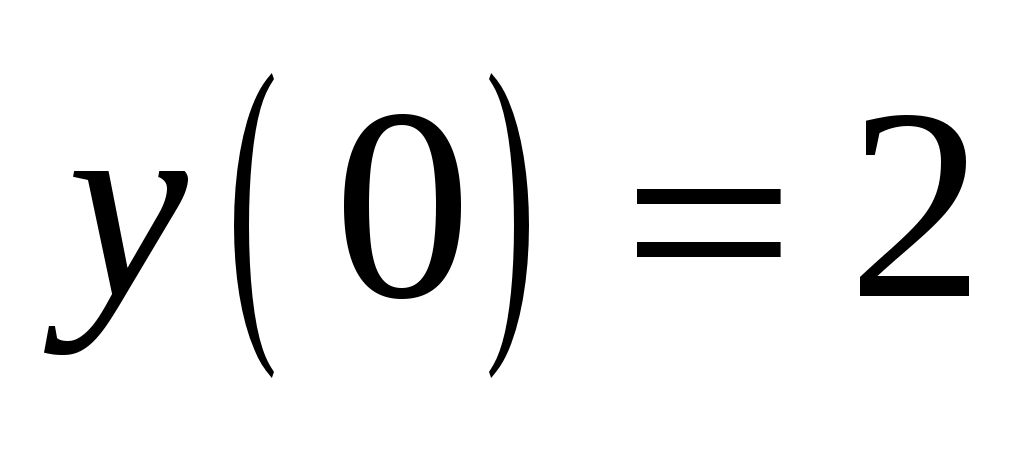 ,
, 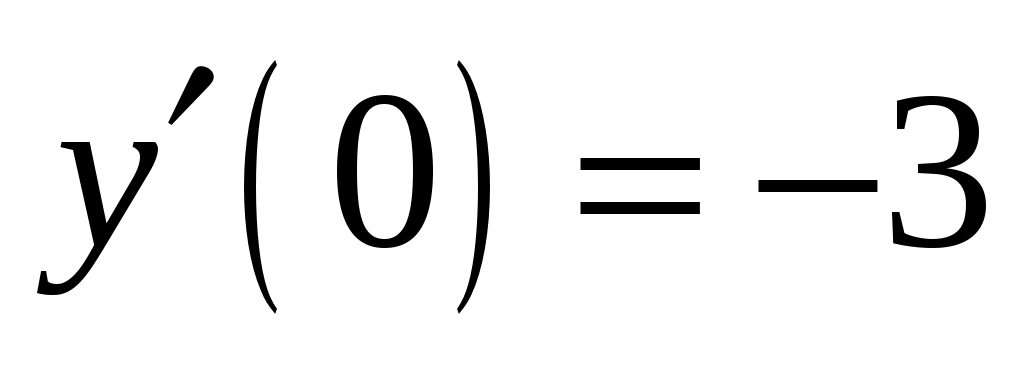 .
.
Решение.
Запишем характеристическое уравнение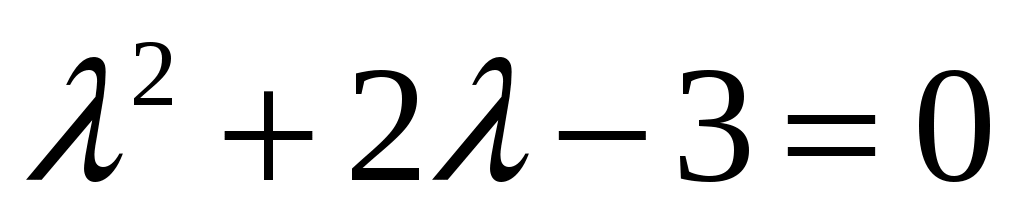 . Корни этого уравнения равны
. Корни этого уравнения равны 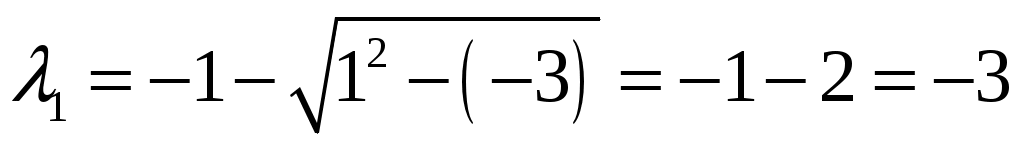 и
и 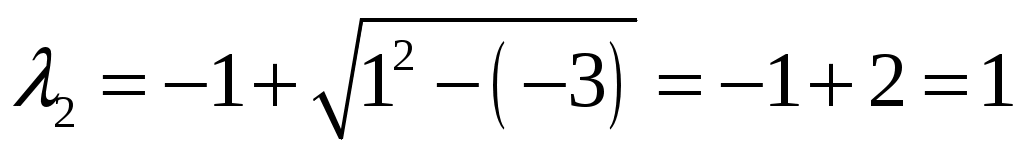 . Тогда общее решение однородного уравнения равно
. Тогда общее решение однородного уравнения равно 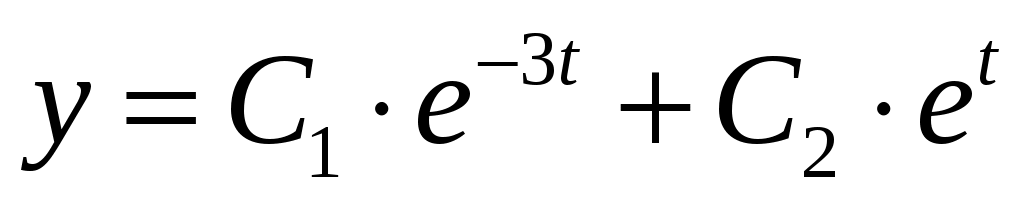 .
.
Найдем частное решение, удовлетворяющее начальным условиям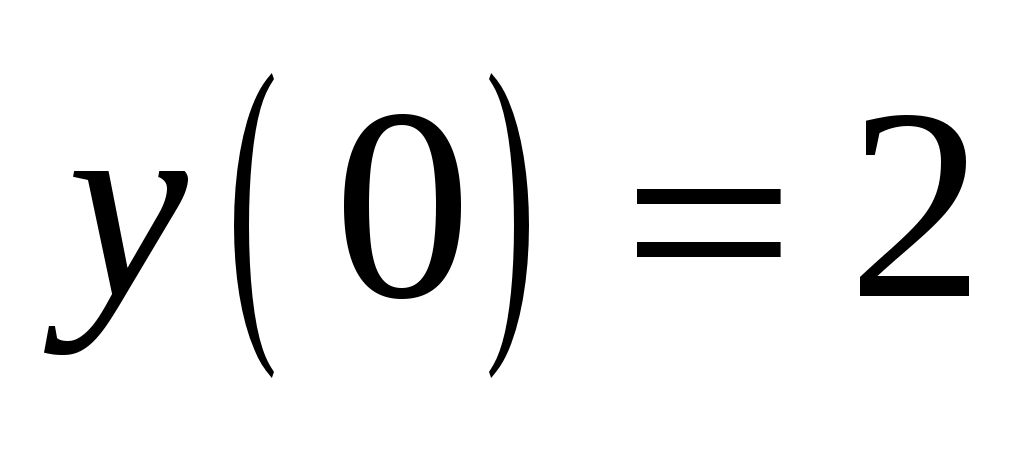 ,
, 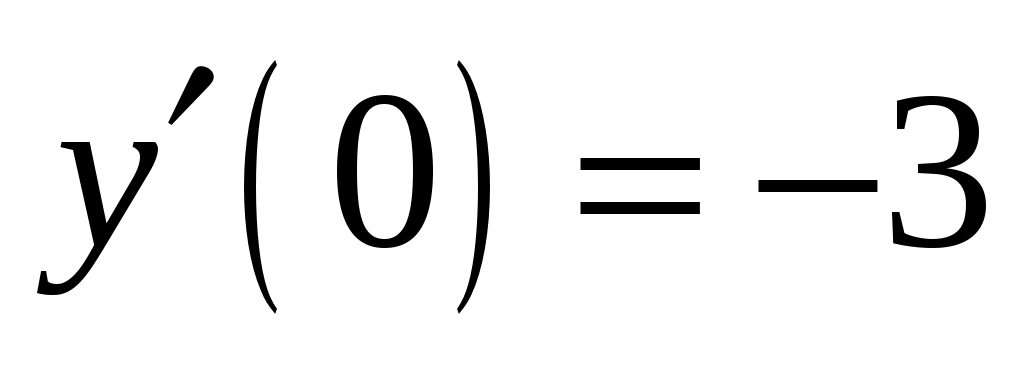 . Вычислим производную функции решения:
. Вычислим производную функции решения:
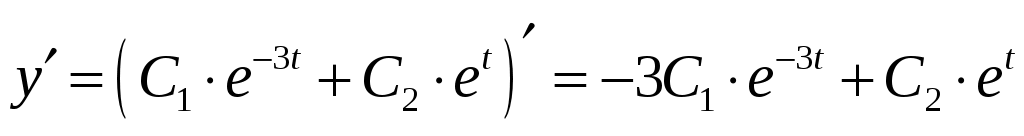 .
.
Тогда получим систему уравнений:
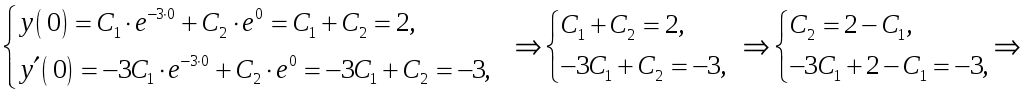
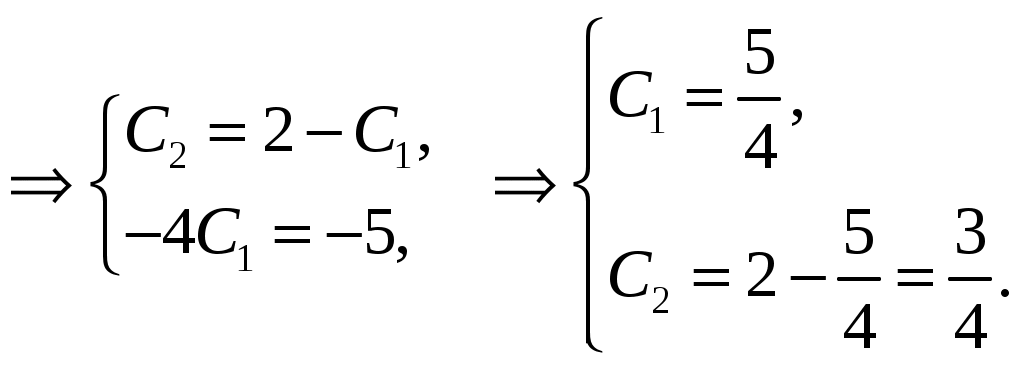
Частное решение равно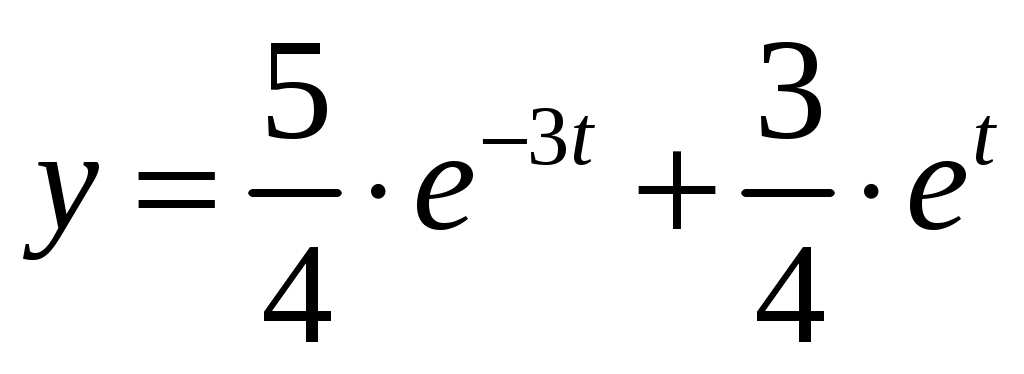 .
.
Ответ: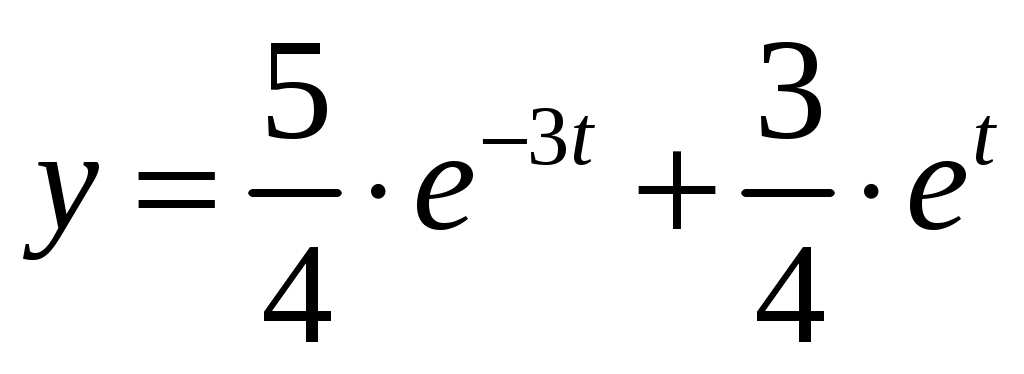 .
.
Задача 52. Найти общее решение линейного ДУ второго порядка, используя метод подбора.
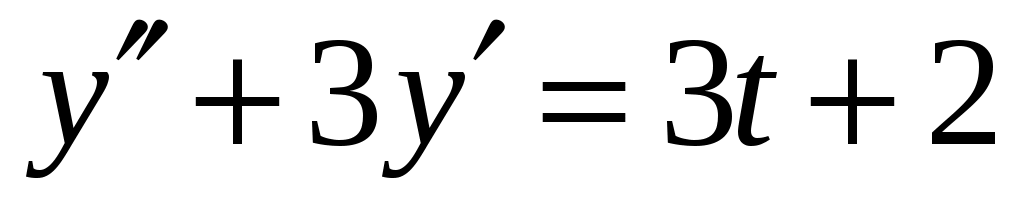 .
.
Решение.
Это линейное неоднородное дифференциальное уравнение с постоянными коэффициентами. Общее решение, которого определяется как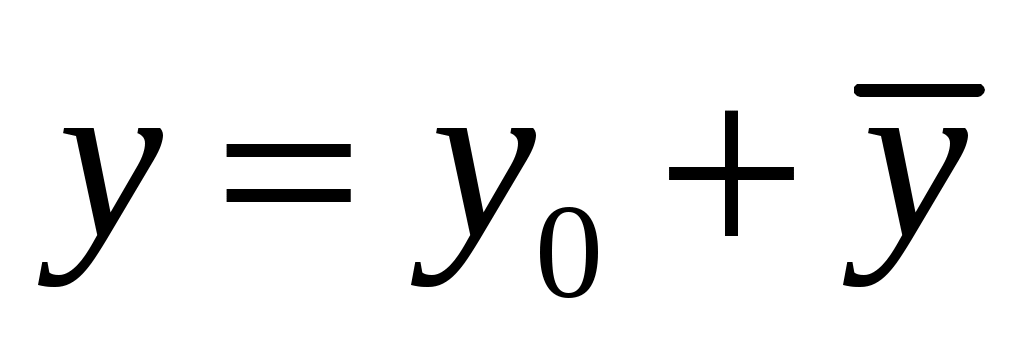 , где
, где 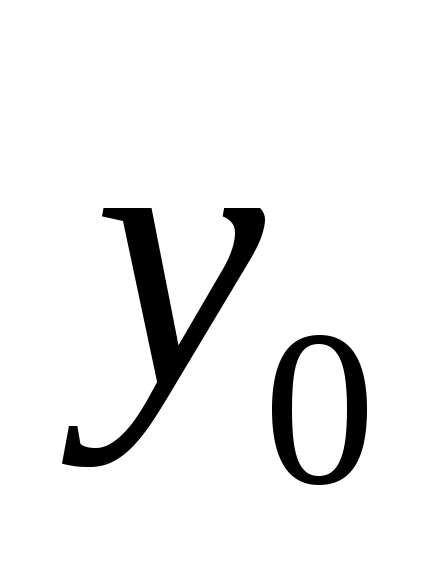 - общее решение однородного уравнения
- общее решение однородного уравнения 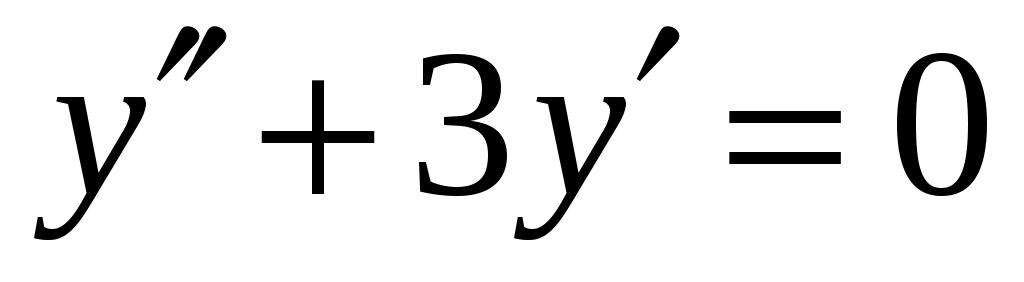 , а
, а 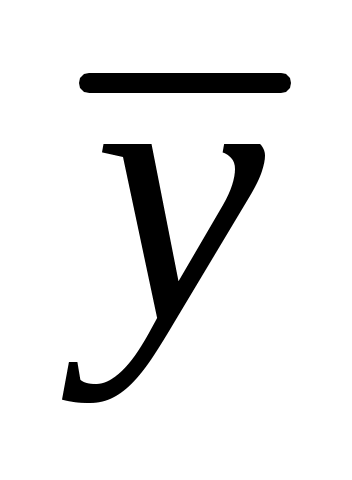 - одно из частных решений исходного уравнения.
- одно из частных решений исходного уравнения.
Найдем общее решение однородного уравнения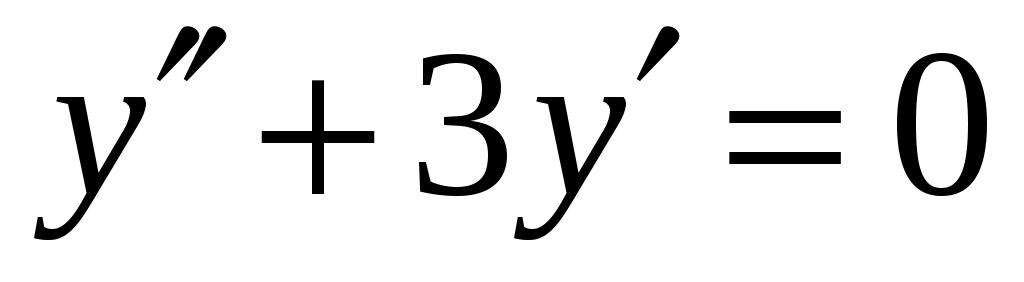 . Запишем характеристическое уравнение
. Запишем характеристическое уравнение 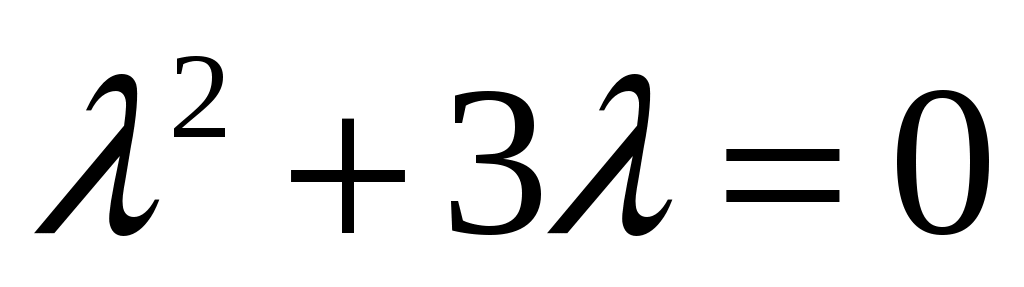
,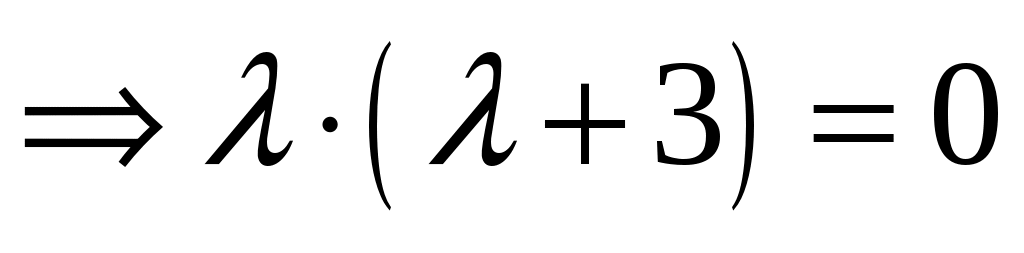 . Корни этого уравнения равны
. Корни этого уравнения равны 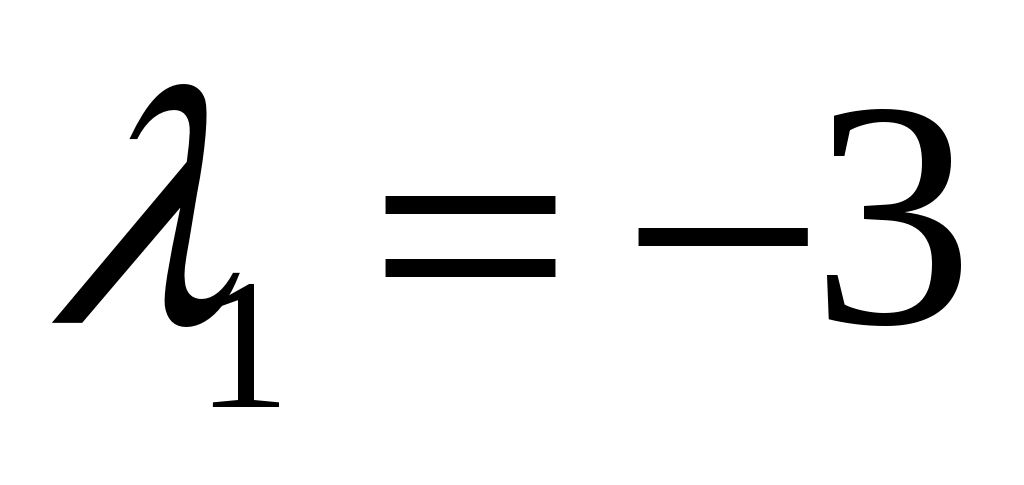 и
и 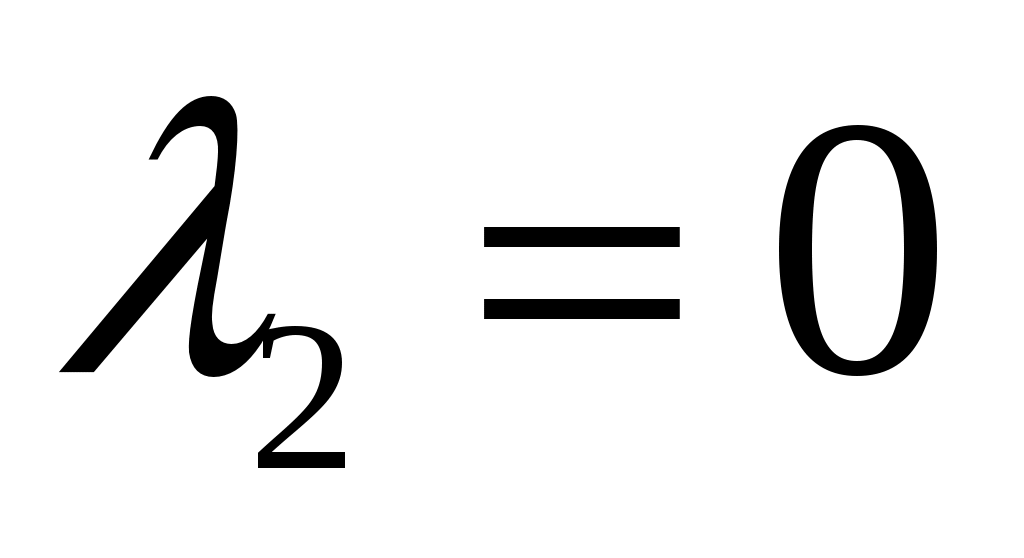 . Тогда общее решение однородного уравнения равно
. Тогда общее решение однородного уравнения равно 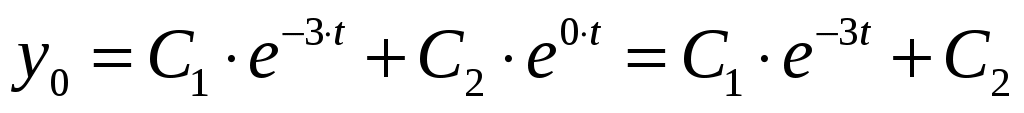 .
.
Так как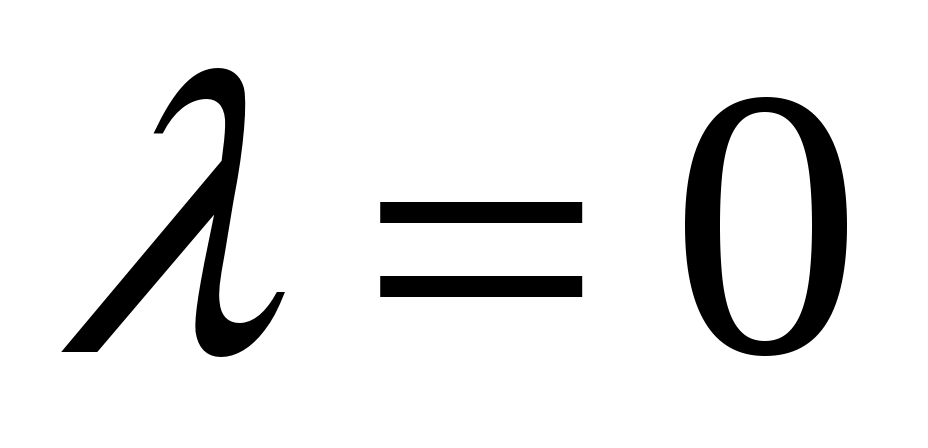 является корнем характеристического уравнения кратности
является корнем характеристического уравнения кратности 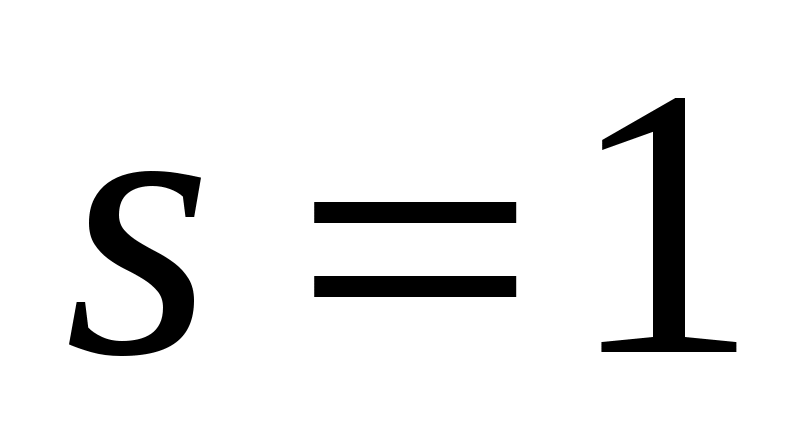 , то частное решение неоднородного уравнения будем искать в виде
, то частное решение неоднородного уравнения будем искать в виде 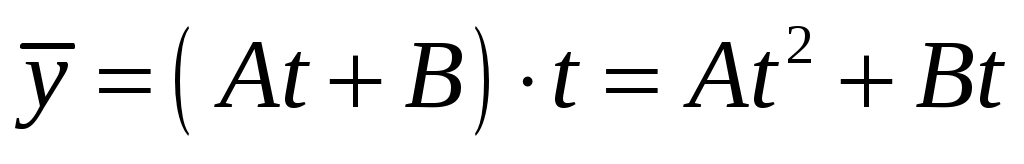 . Вычислим производную до второго порядка включительно, получим:
. Вычислим производную до второго порядка включительно, получим:
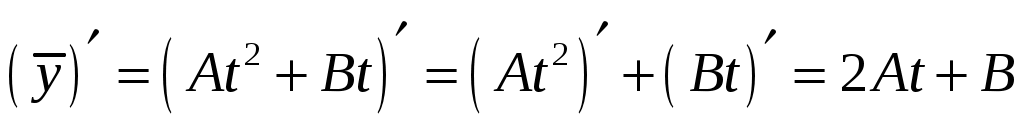 ;
;
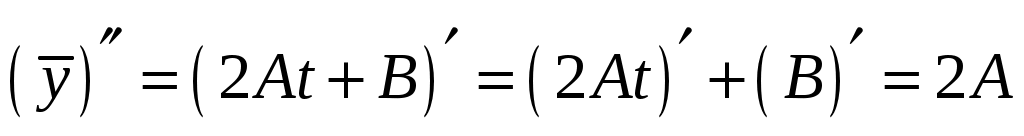 .
.
Полученные выражения для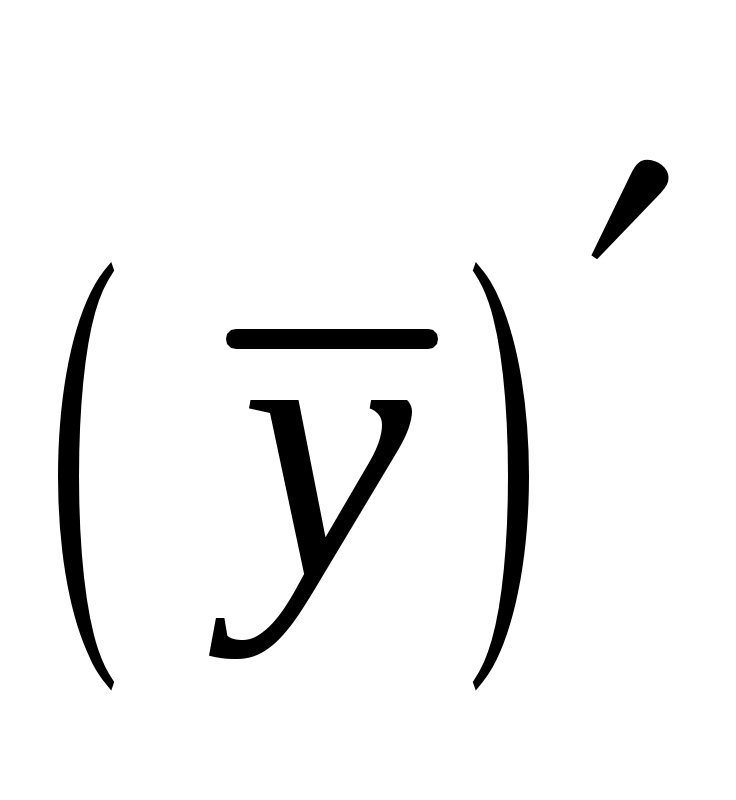 и
и 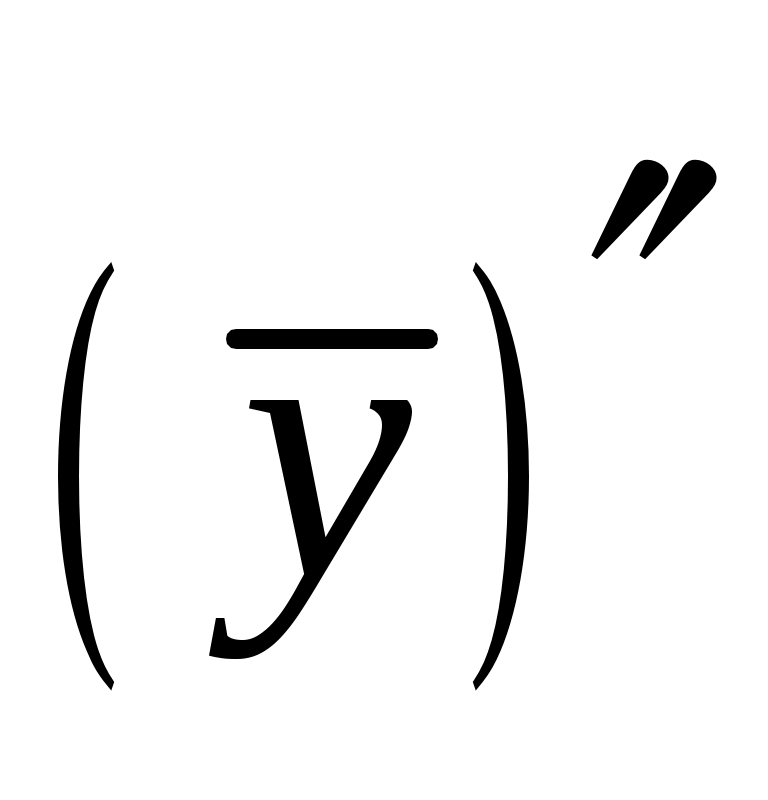 подставим в исходное уравнение, имеем:
подставим в исходное уравнение, имеем:
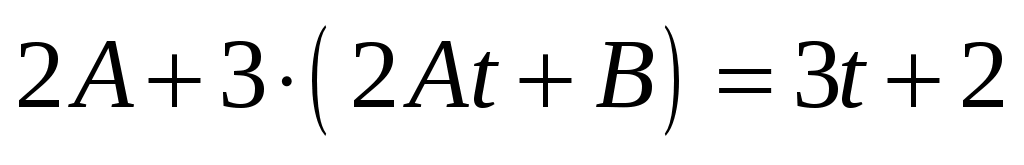 ;
;
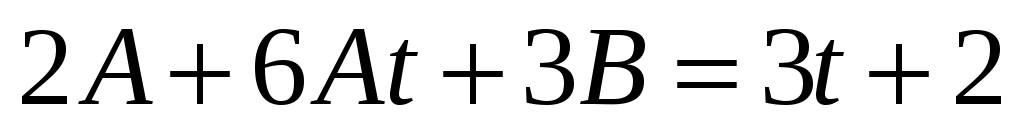 .
.
Составим систему уравнений и найдем его решение:
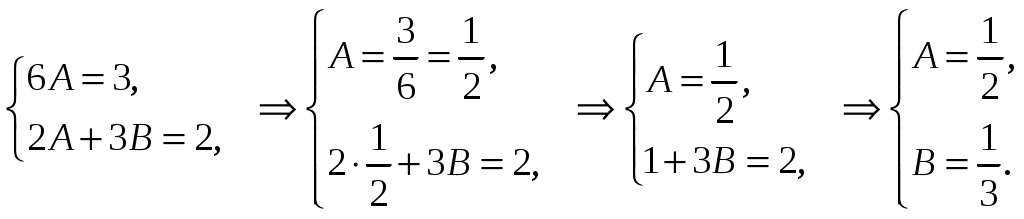
Частное решение равно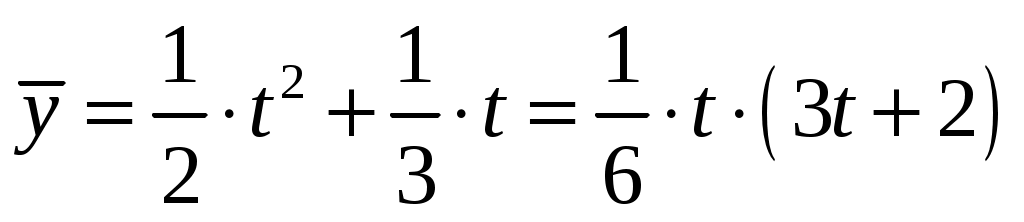 .
.
Общий интеграл исходного уравнения равен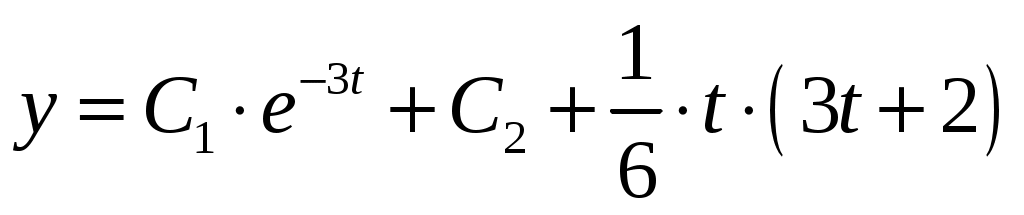 .
.
Ответ: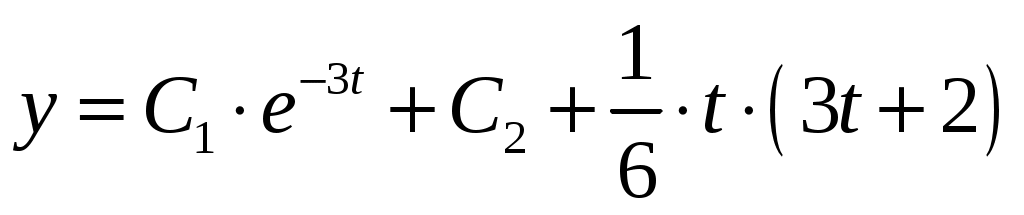 .
.
Задача 62. Для данного ряда найти: а) радиус сходимости и указать область сходимости ряда; б) выписать первые три члена ряда.
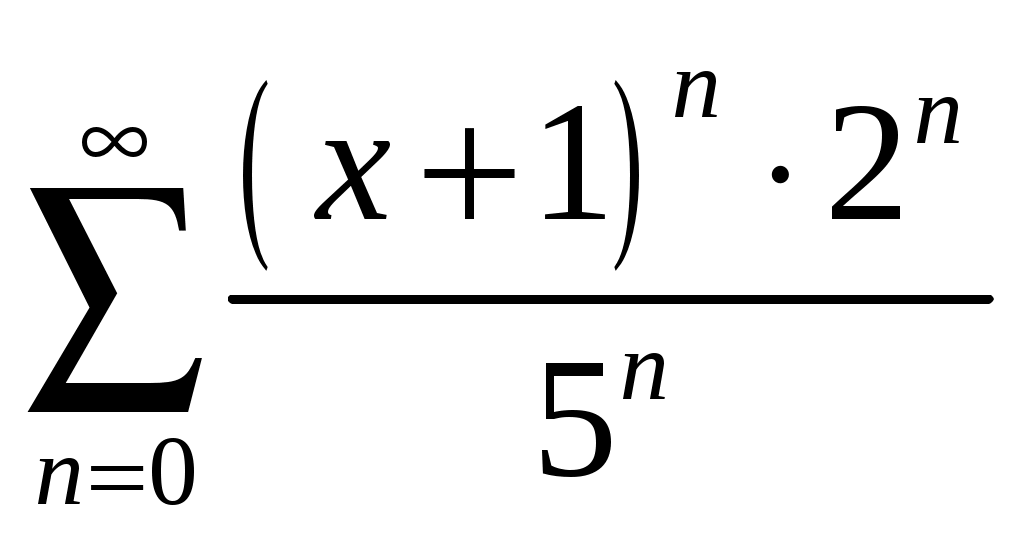 .
.
Решение.
а) Найдем радиус сходимости по признаку Даламбера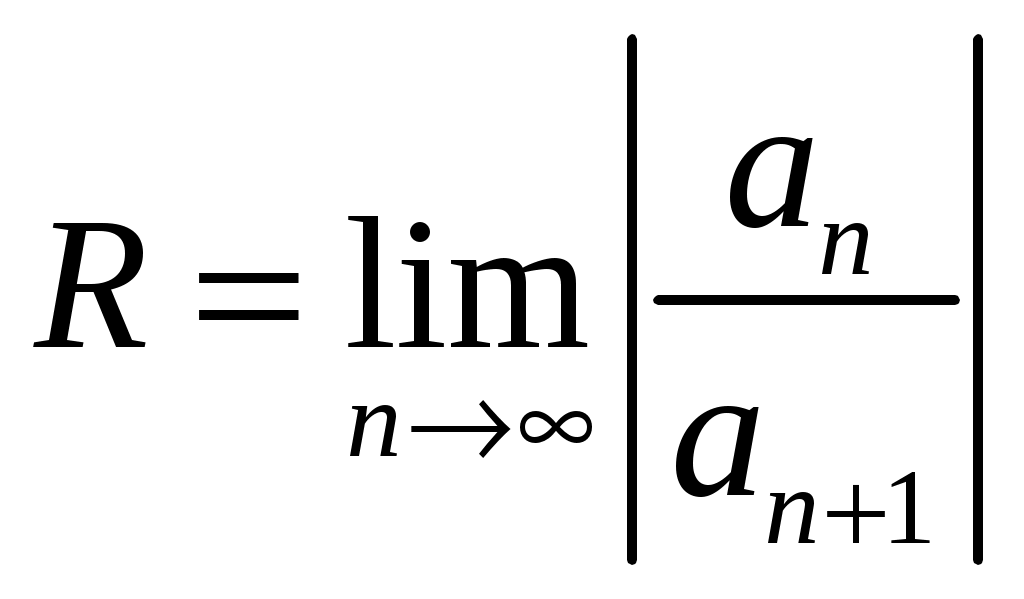 . Для данного ряда
. Для данного ряда 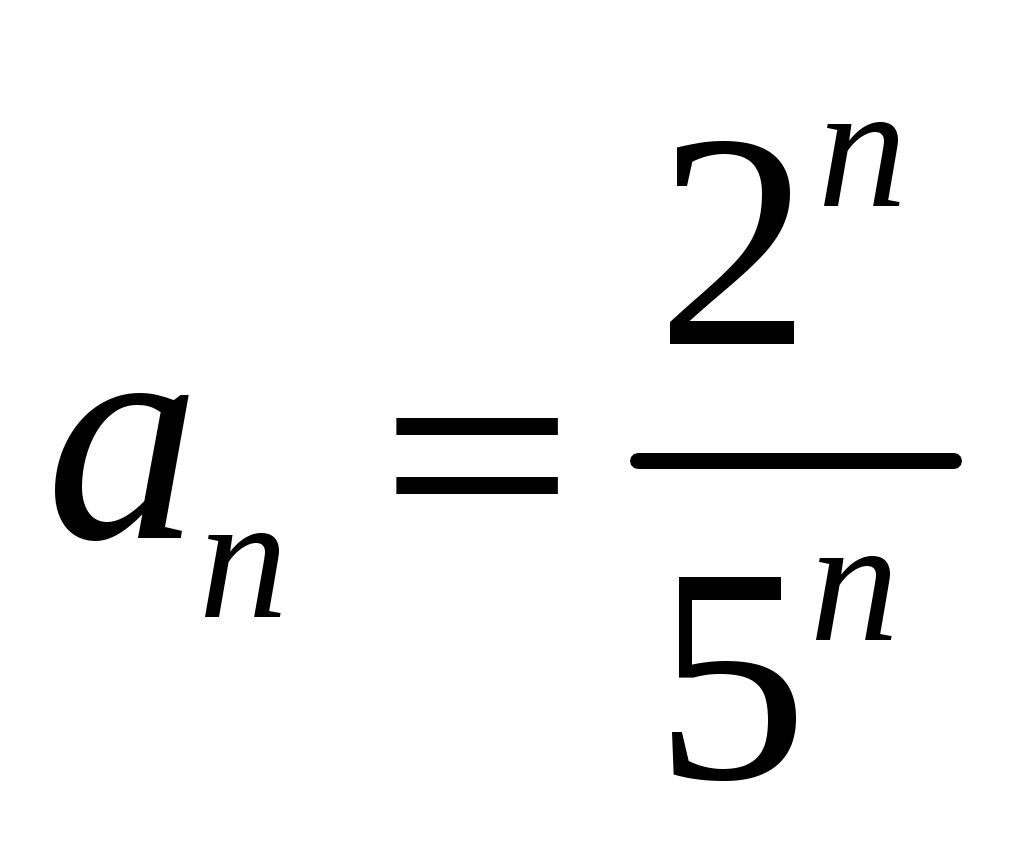 и
и 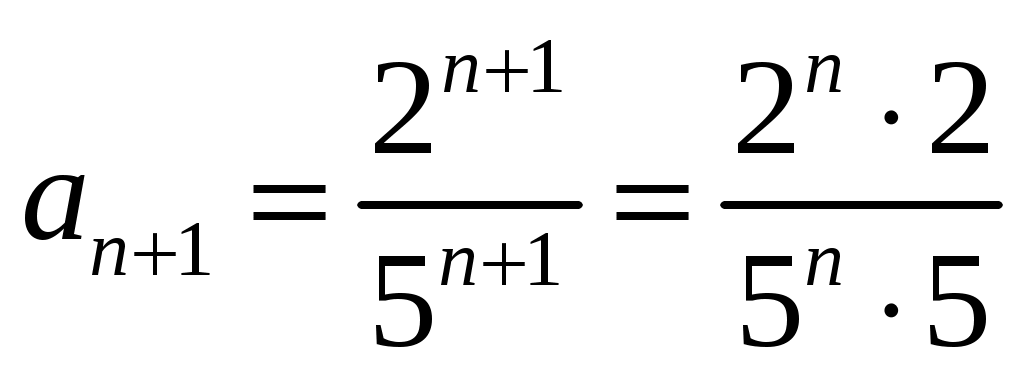
, тогда получим: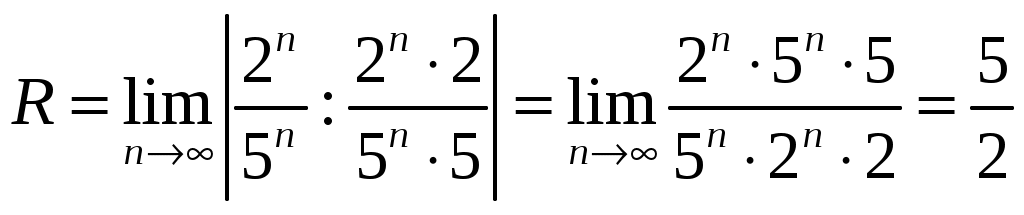 .
.
Радиус сходимости ряда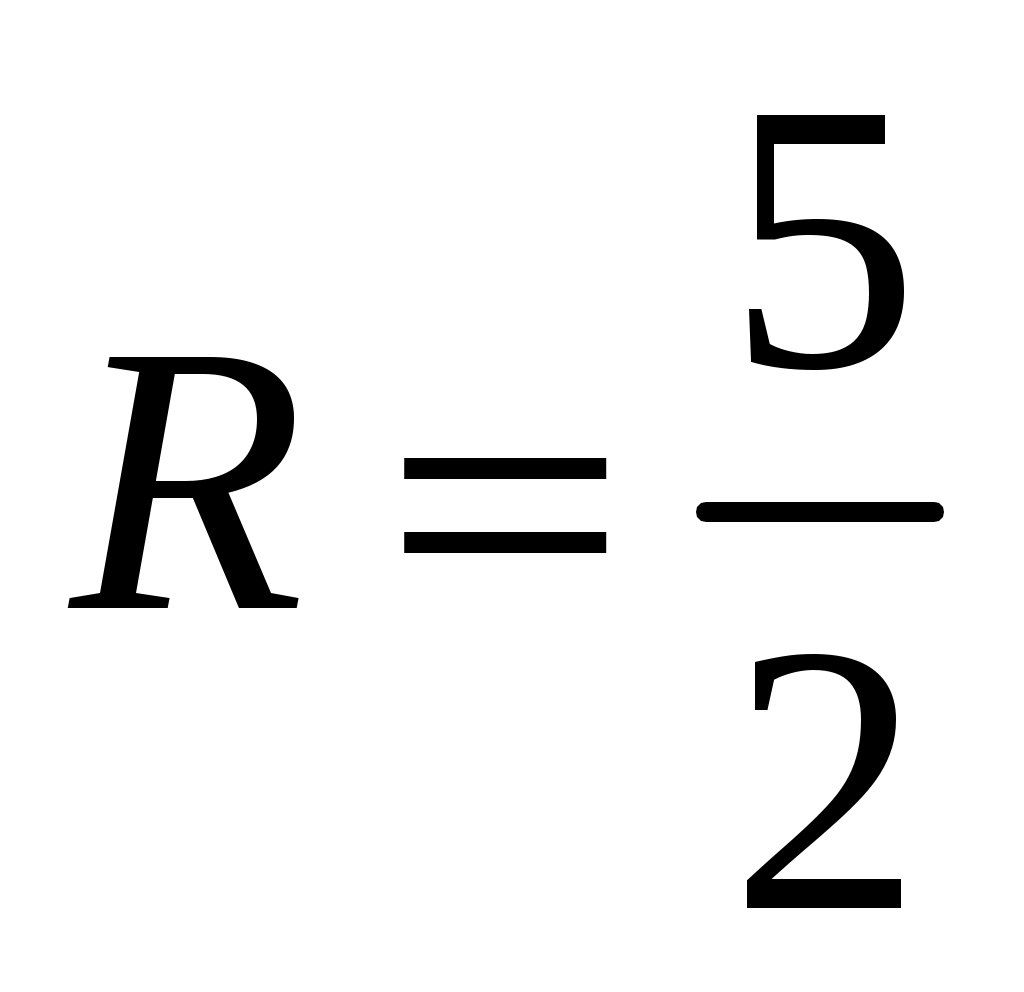 . Интервал сходимости равен
. Интервал сходимости равен 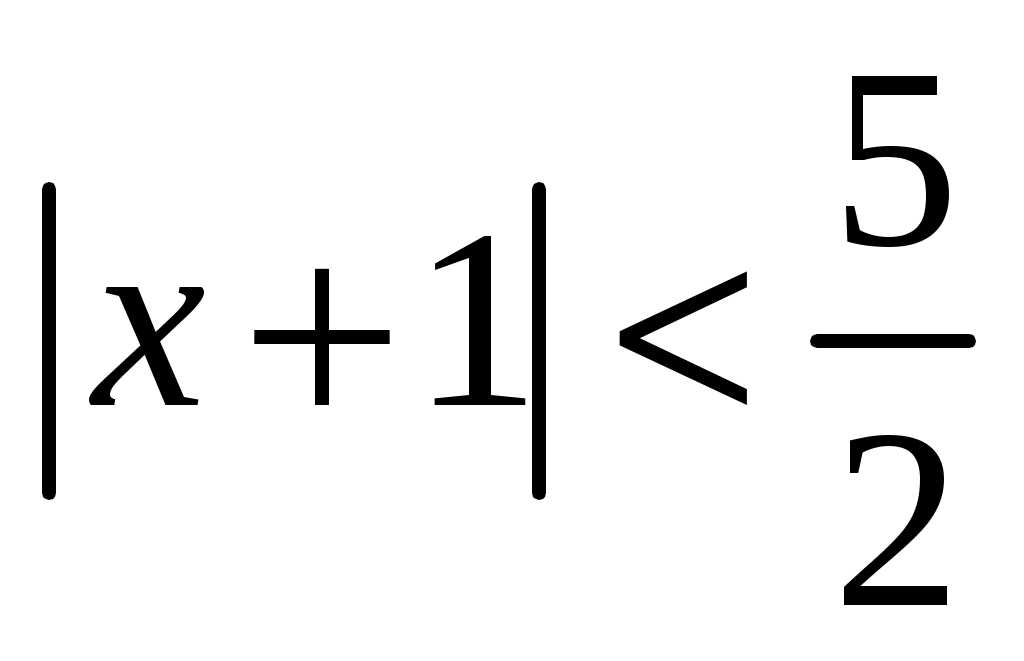 ,
, 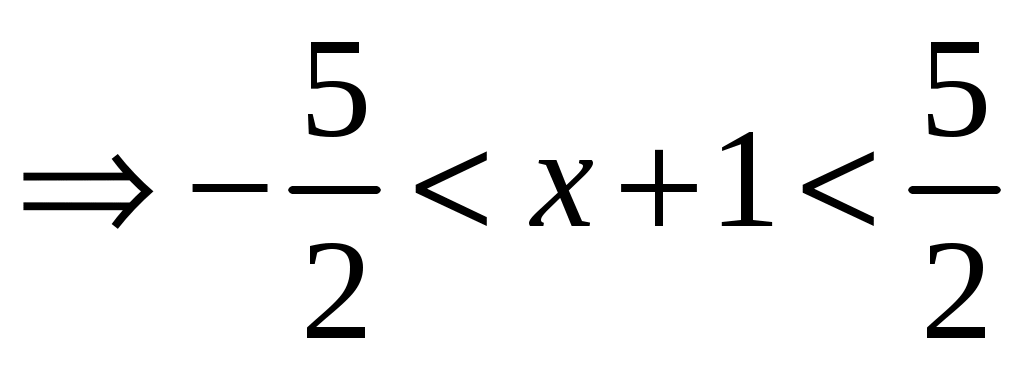 ,
, 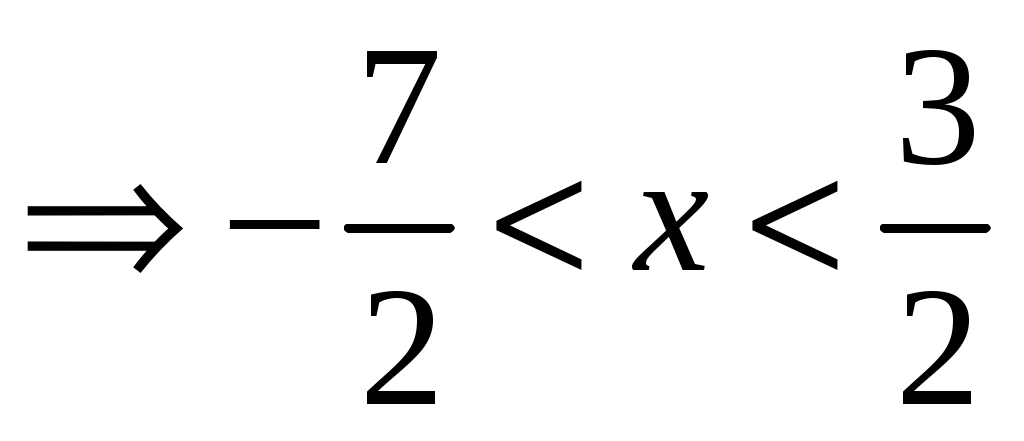 . Итак, интервал сходимости степенного ряда
. Итак, интервал сходимости степенного ряда 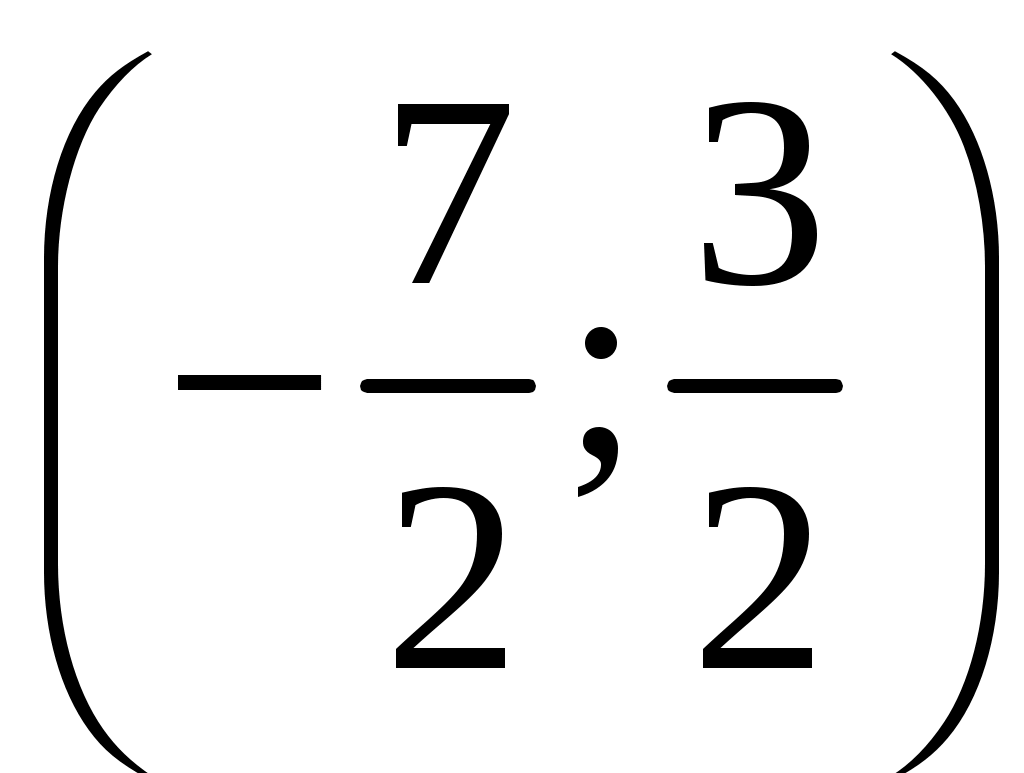 . Исследуем ряд на сходимость в граничных точках
. Исследуем ряд на сходимость в граничных точках 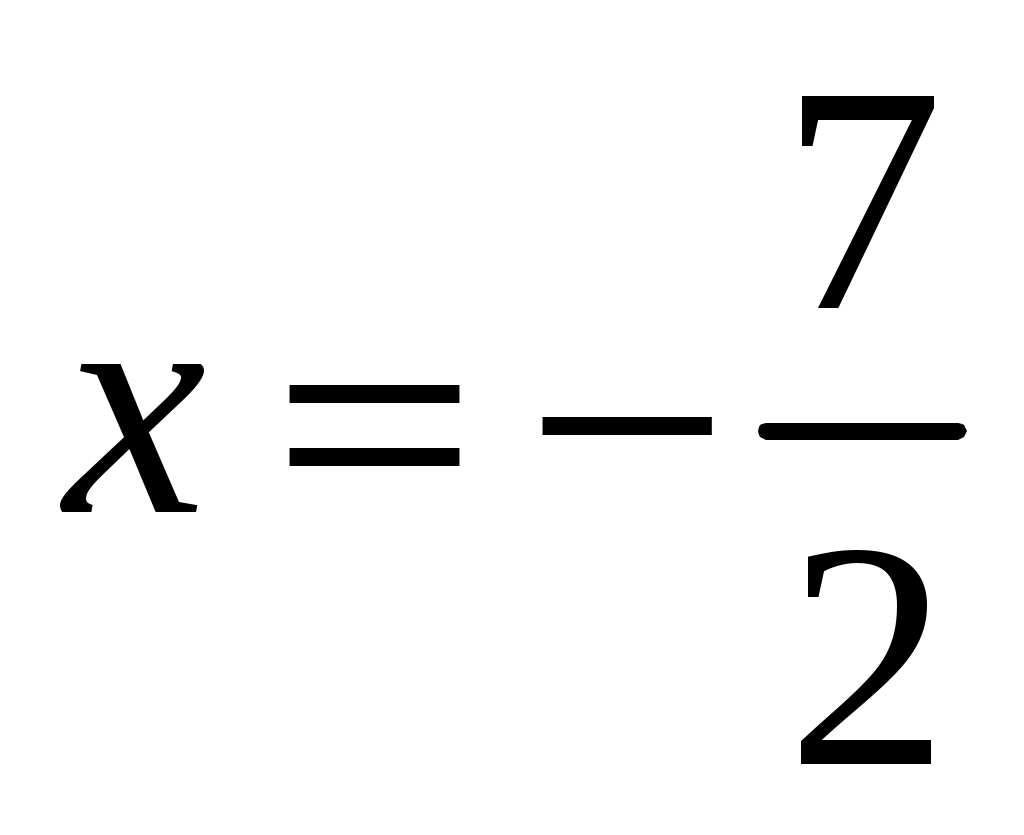 и
и 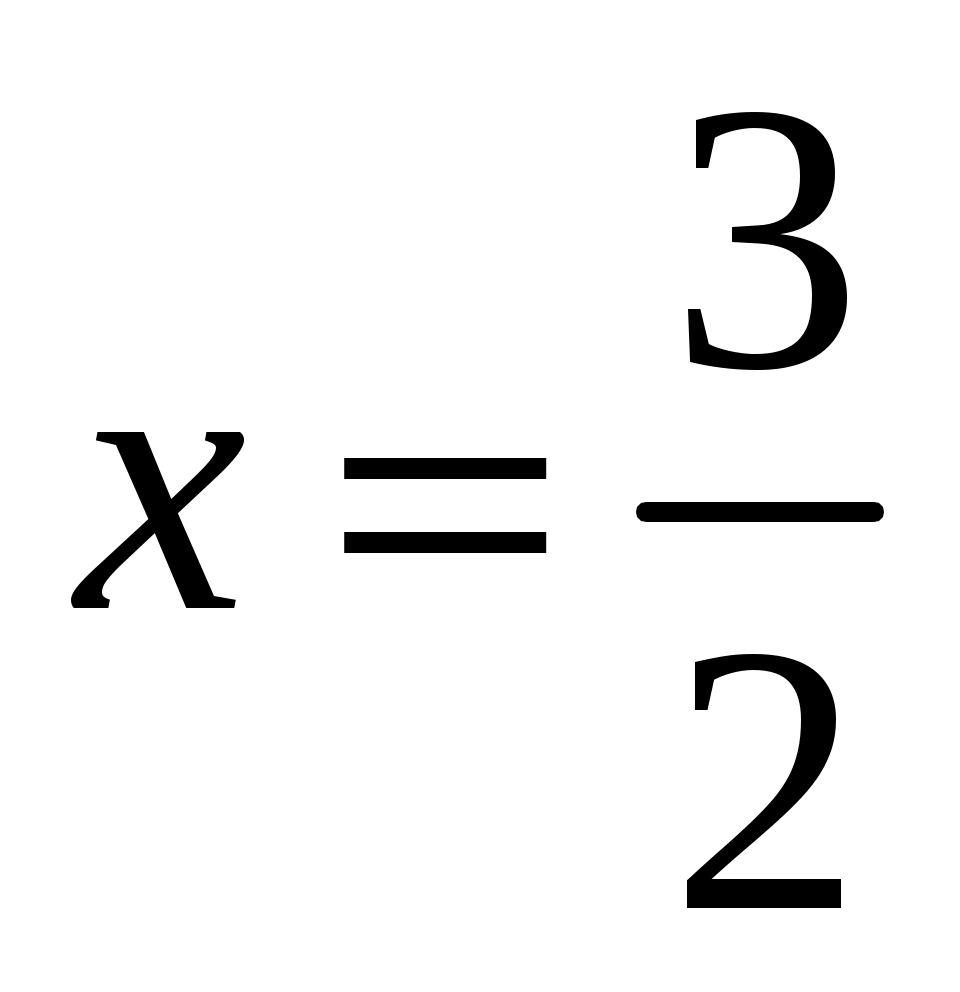 .
.
1) Пусть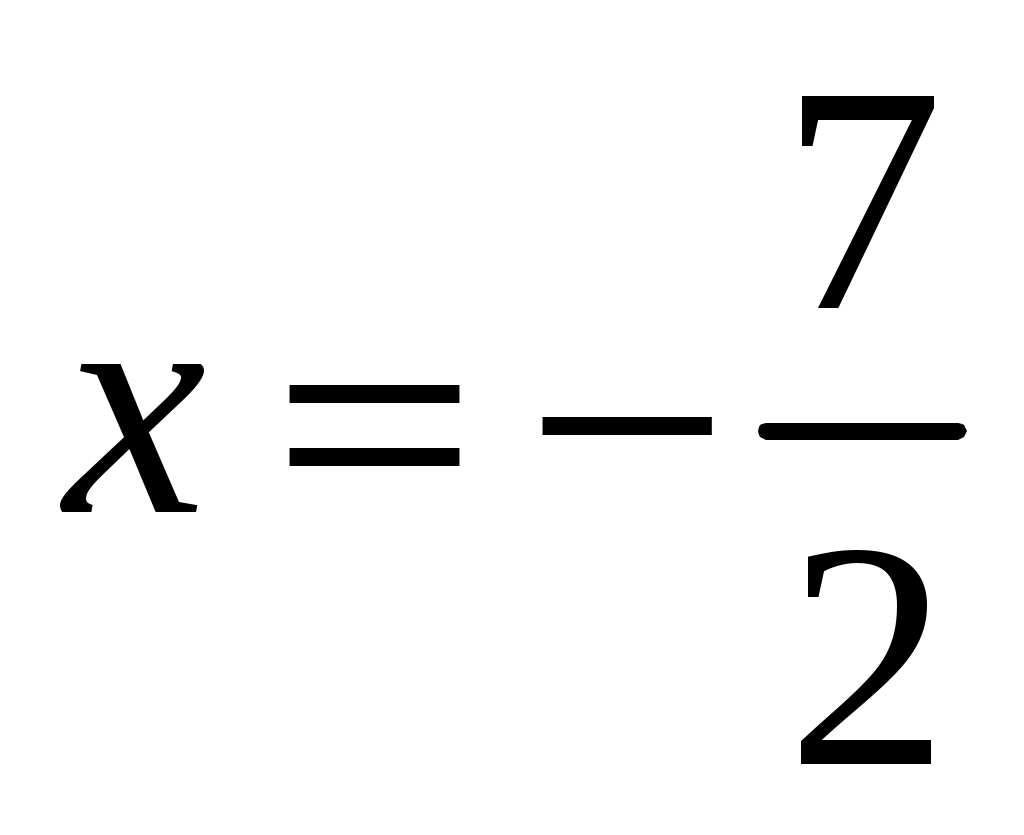 . Подставим x в ряд, получим:
. Подставим x в ряд, получим: 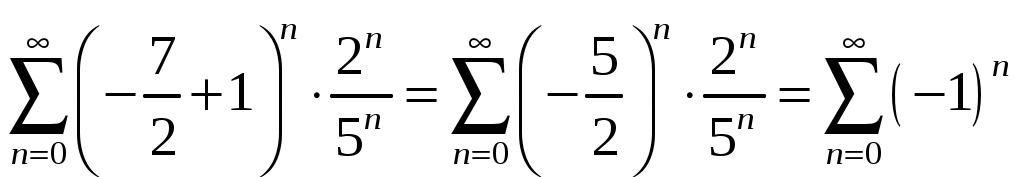 .
.
Исследуем на сходимость по признаку Лейбница. Проверив выполнений признака.
1)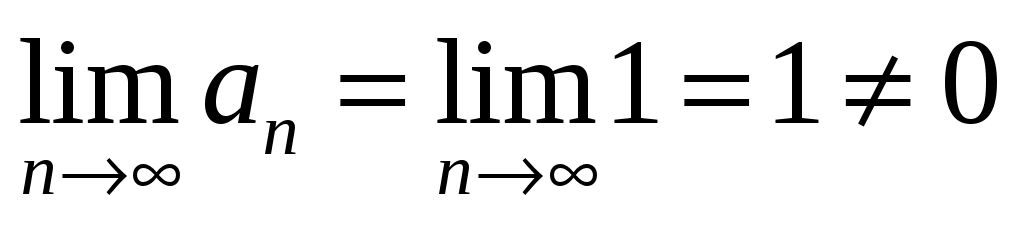 ,
,
Ряд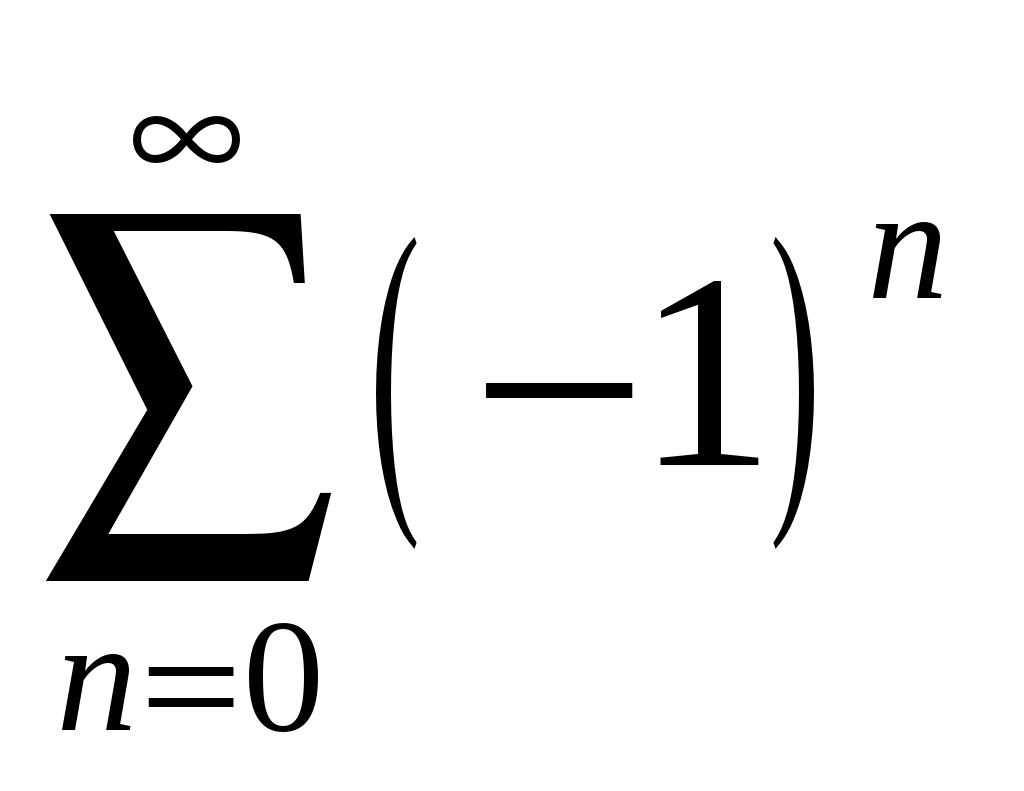 расходится.
расходится.
2) Пусть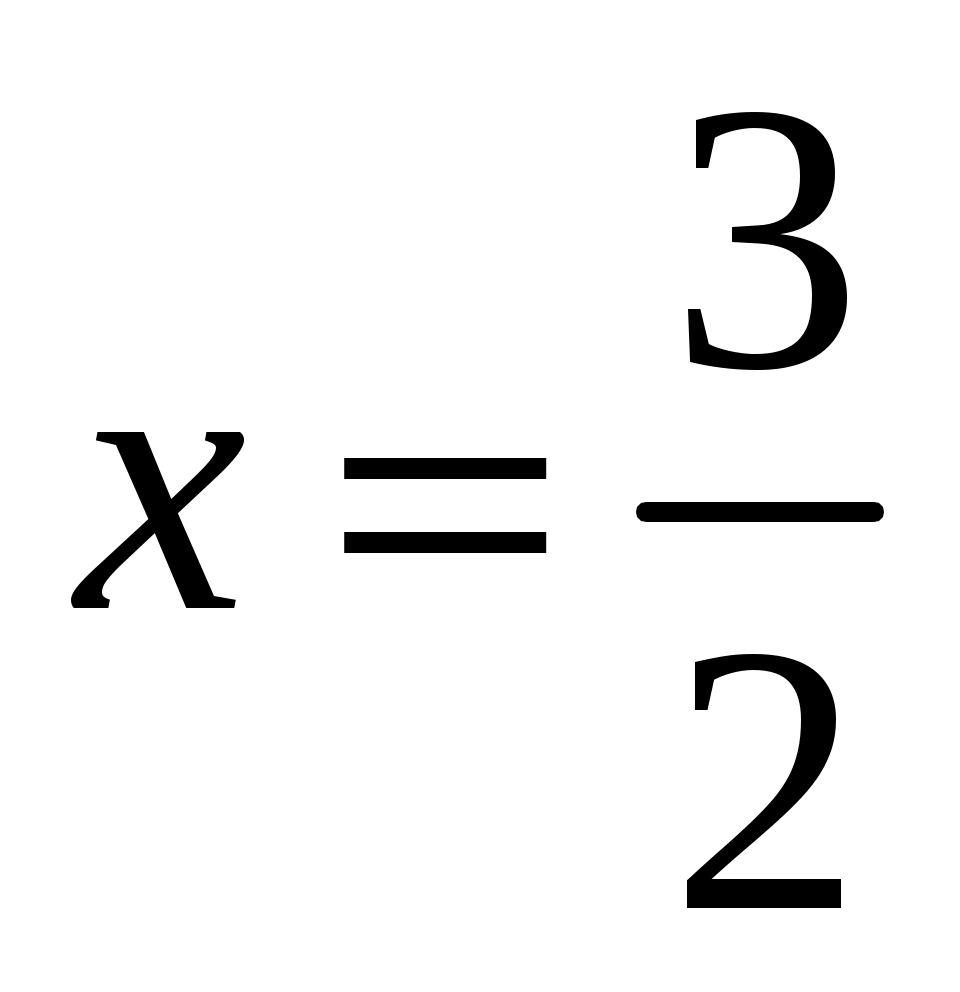 . Подставим x в ряд, получим
. Подставим x в ряд, получим 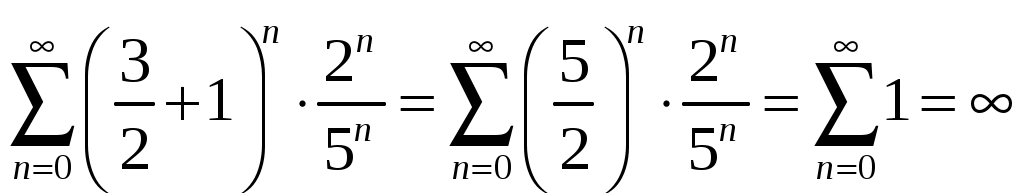 . Полученный ряд расходится.
. Полученный ряд расходится.
Следовательно, исходный ряд сходится на интервале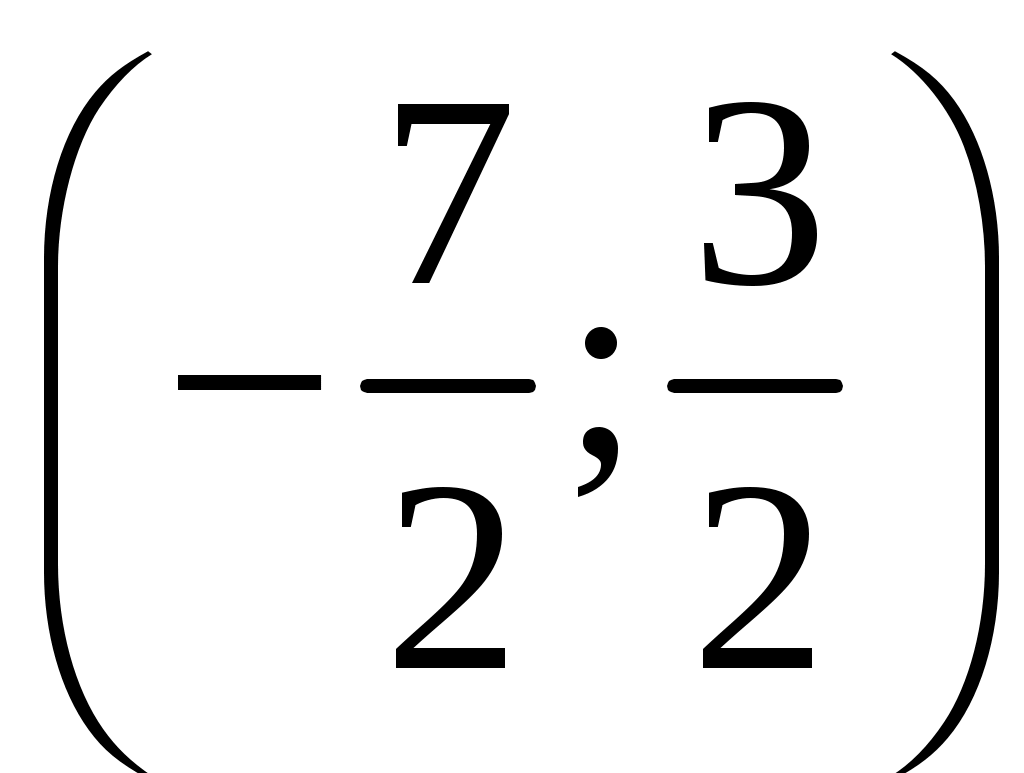 .
.
б) Выпишем первые три члена ряда.
При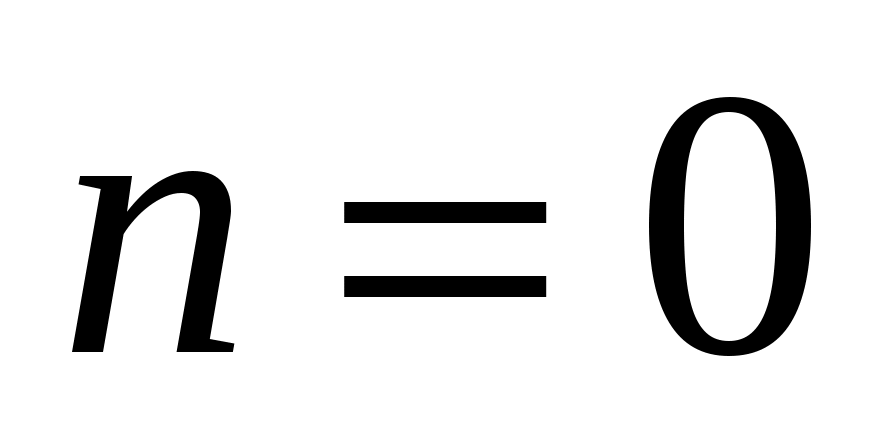 , имеем
, имеем 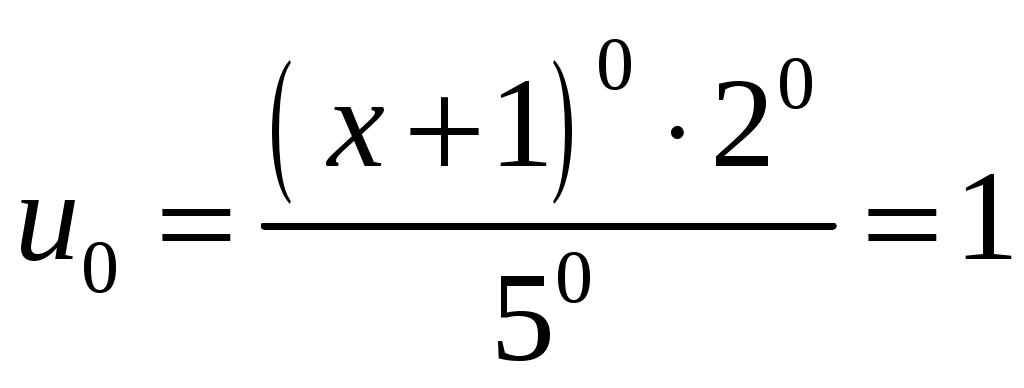 ; при
; при 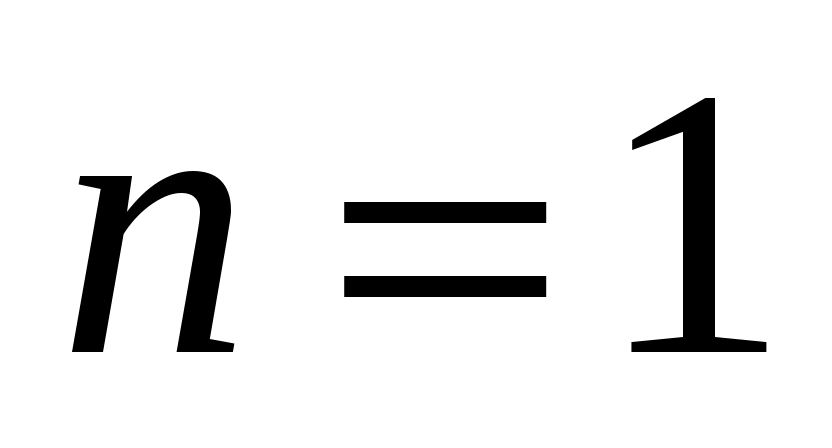 , имеем
, имеем 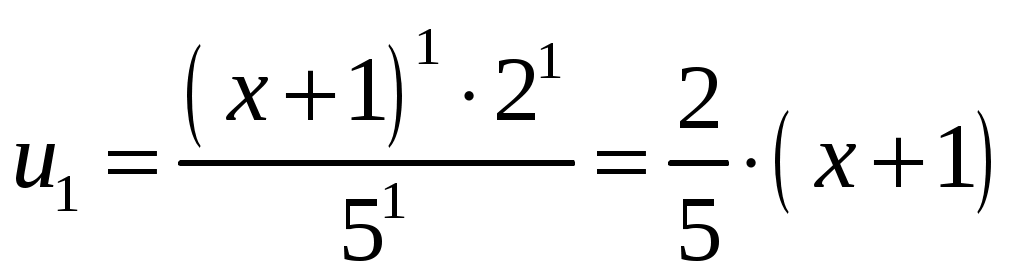 ; при
; при 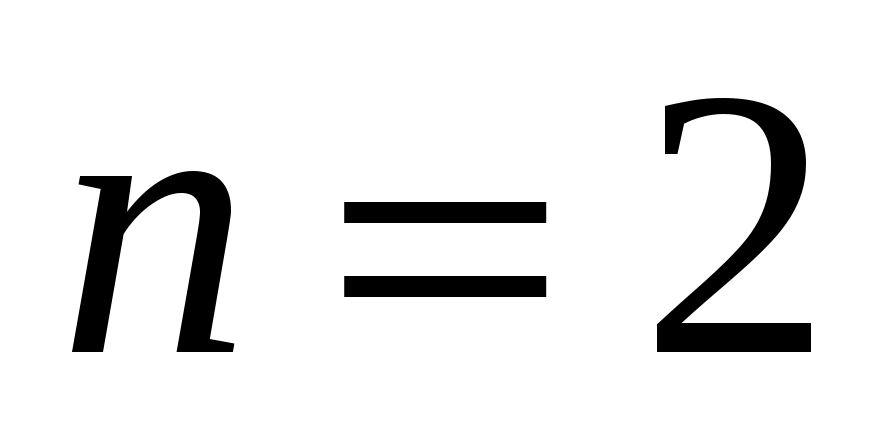 , имеем
, имеем 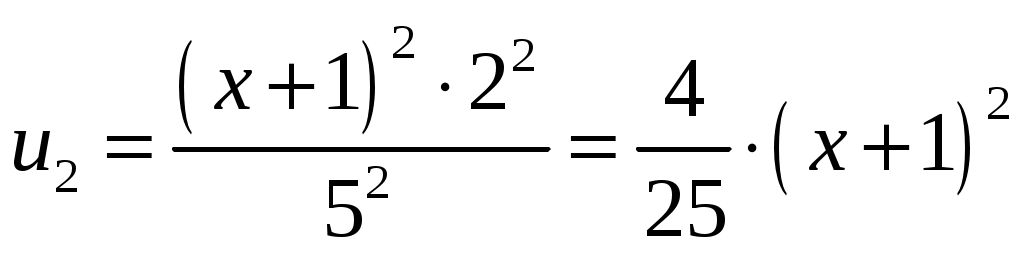 ; при
; при 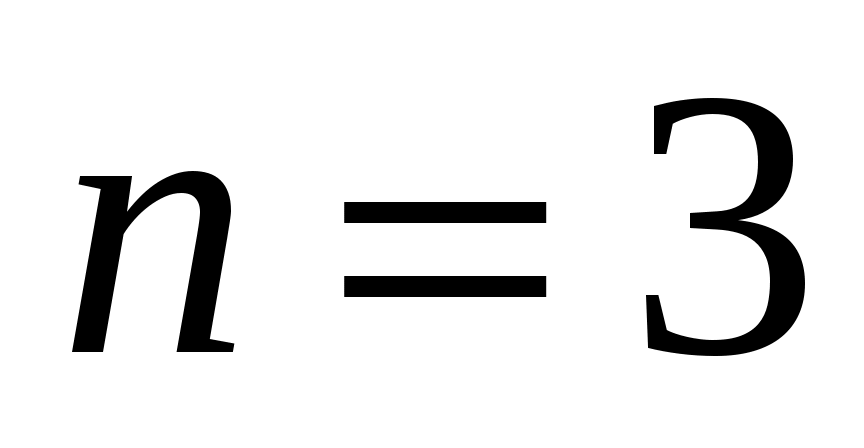 , имеем
, имеем 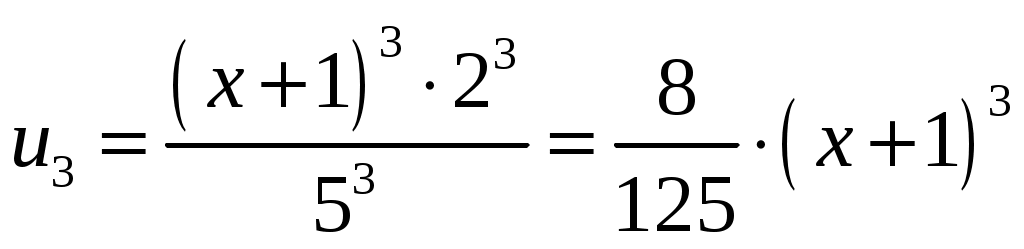
.
Тогда получим ряд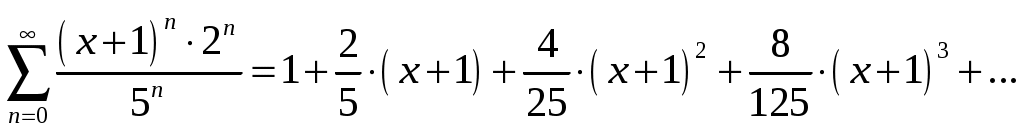 .
.
Ответ: а) радиус сходимости и ряд сходится на интервале
и ряд сходится на интервале  ;
;
б)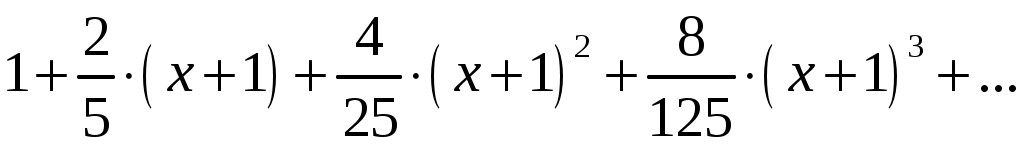 .
.
Задача 72. Найти первые пять (ненулевых) членов разложения в степенной ряд решение ДУ с заданными начальными условиями:
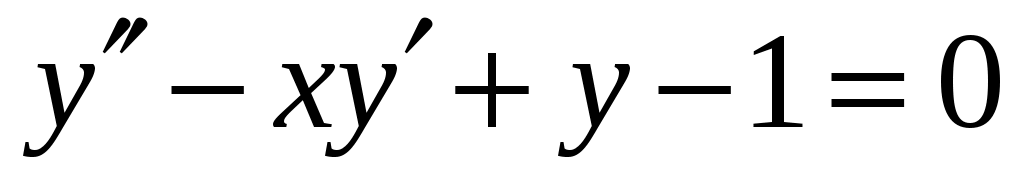 ,
,  ,
, 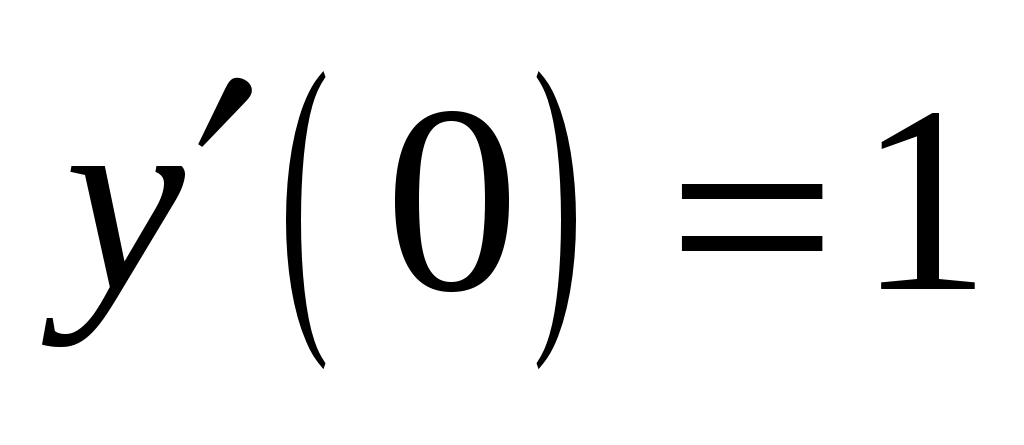 .
.
Решение.
Так как начальные условия заданы в точке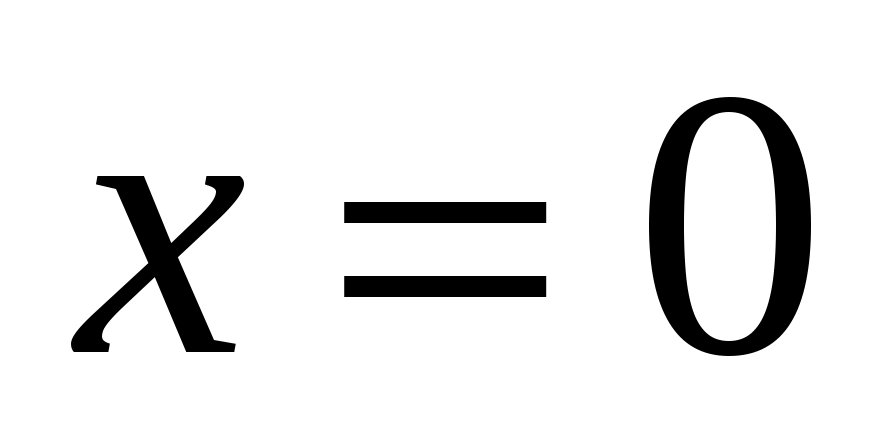 , ищем решение в виде ряда Маклорена
, ищем решение в виде ряда Маклорена 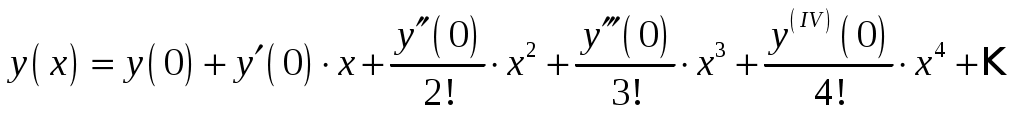
Поскольку и
и 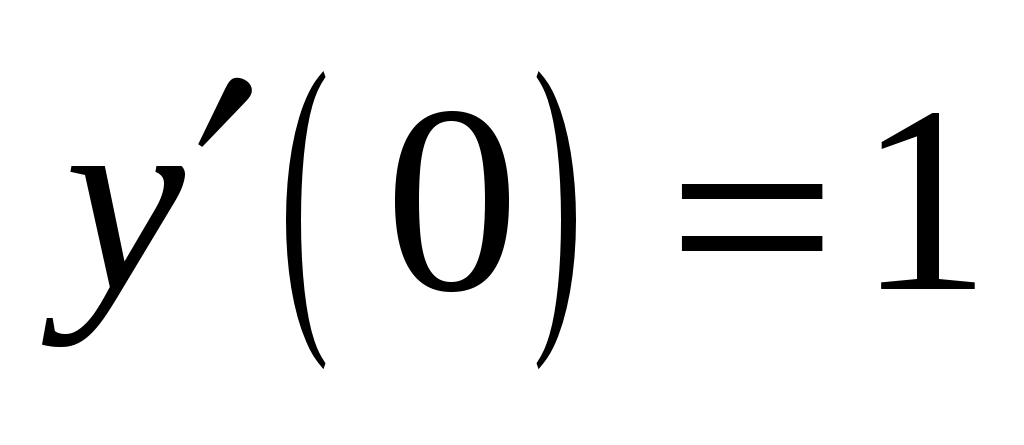 , то согласно уравнению
, то согласно уравнению 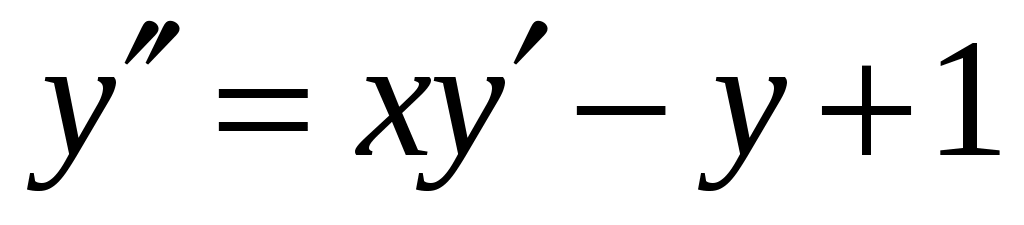 получим:
получим: 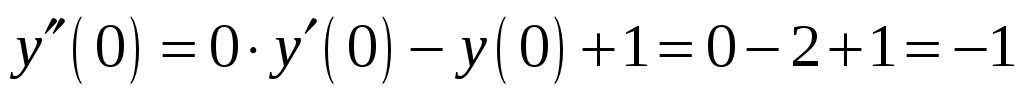 .
.
Продифференцируем по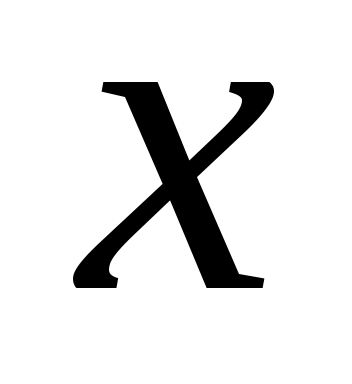 обе части равенства
обе части равенства 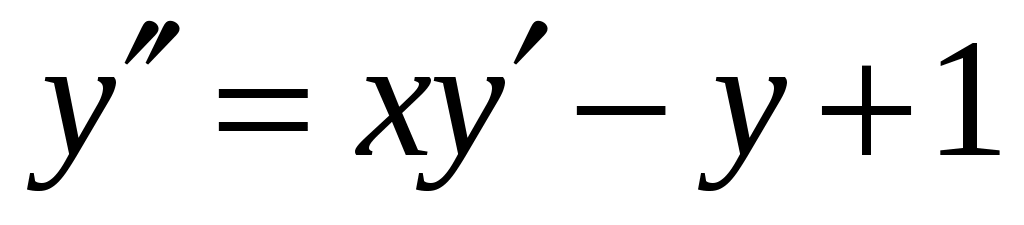 , получим:
, получим: 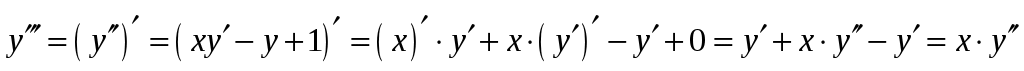 . Подставляя в него
. Подставляя в него 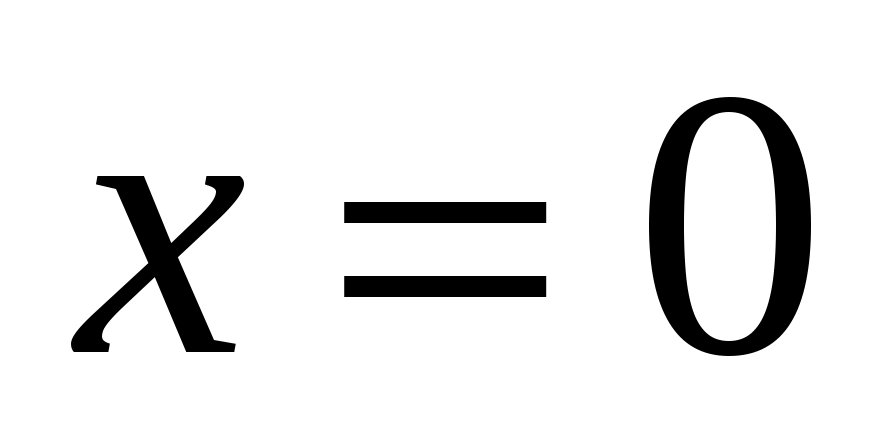 , получаем
, получаем 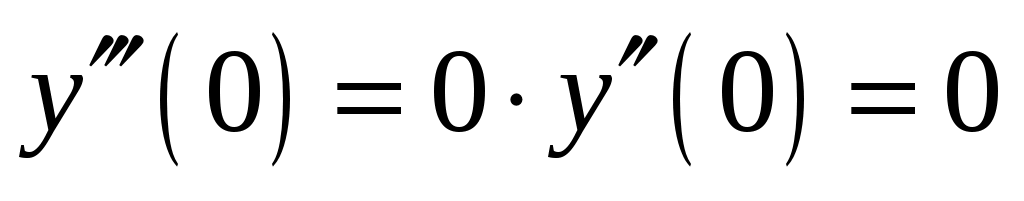 .
.
Продифференцируем по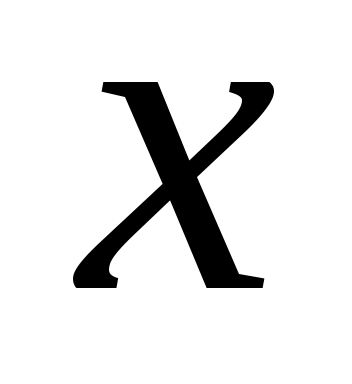 обе части равенства
обе части равенства 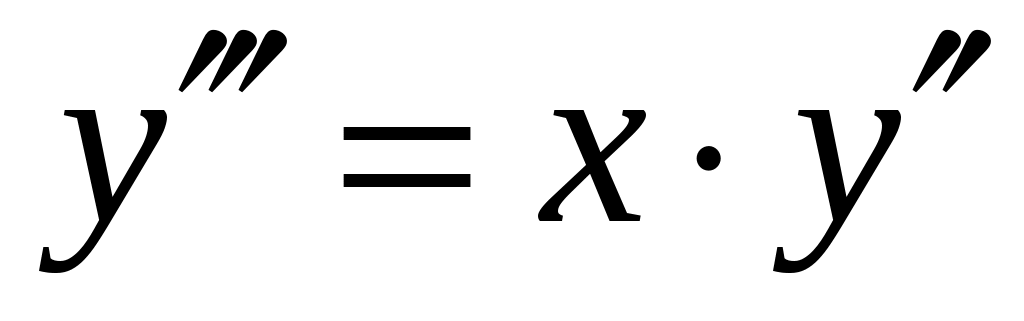 , получим:
, получим: 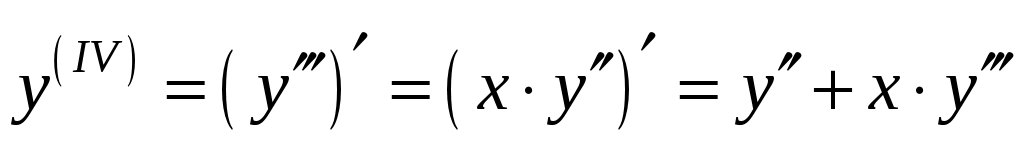 . Подставляя в него
. Подставляя в него 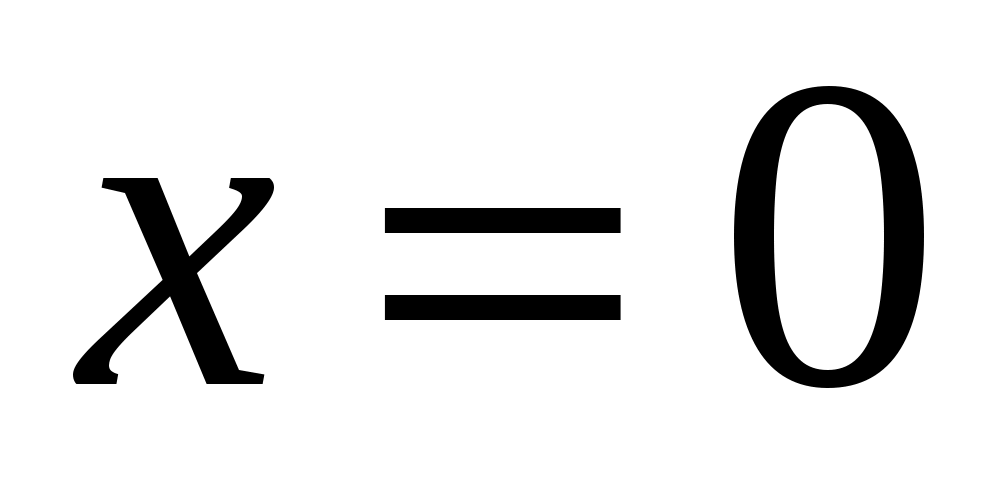 , получаем
, получаем 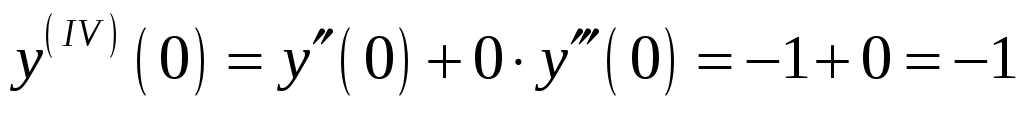
Решение.
Сначала найдем общее решение однородного уравнения
Общее решение исходного уравнения будем искать в виде
Интегрируем
Найдем частное решение, удовлетворяющее начальному условию
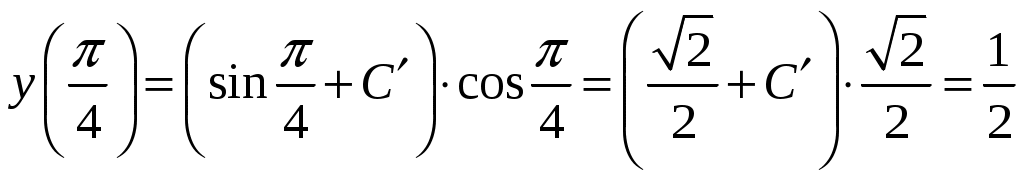 ,
, Частное решение равно
Ответ:
Задача 42. Найти частное решение линейного однородного ДУ второго порядка.
,
Решение.
Запишем характеристическое уравнение
Найдем частное решение, удовлетворяющее начальным условиям
Тогда получим систему уравнений:
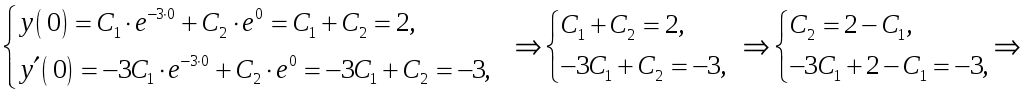
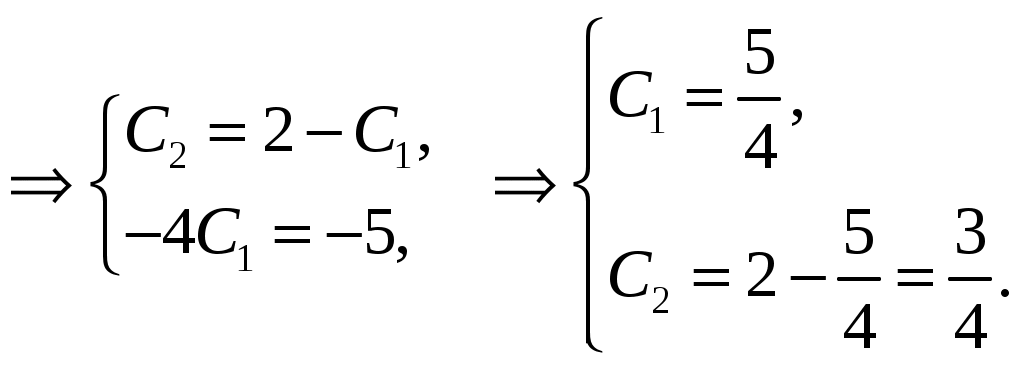
Частное решение равно
Ответ:
Задача 52. Найти общее решение линейного ДУ второго порядка, используя метод подбора.
Решение.
Это линейное неоднородное дифференциальное уравнение с постоянными коэффициентами. Общее решение, которого определяется как
Найдем общее решение однородного уравнения
,
Так как
Полученные выражения для
Составим систему уравнений и найдем его решение:
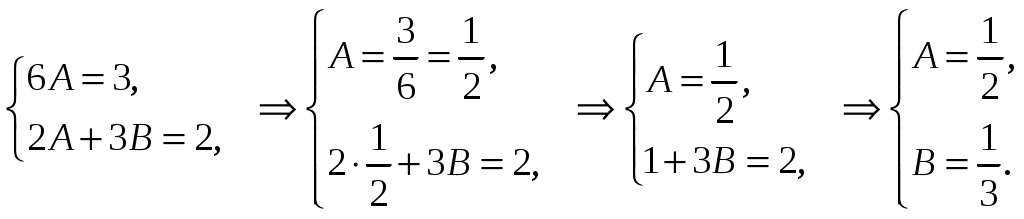
Частное решение равно
Общий интеграл исходного уравнения равен
Ответ:
Задача 62. Для данного ряда найти: а) радиус сходимости и указать область сходимости ряда; б) выписать первые три члена ряда.
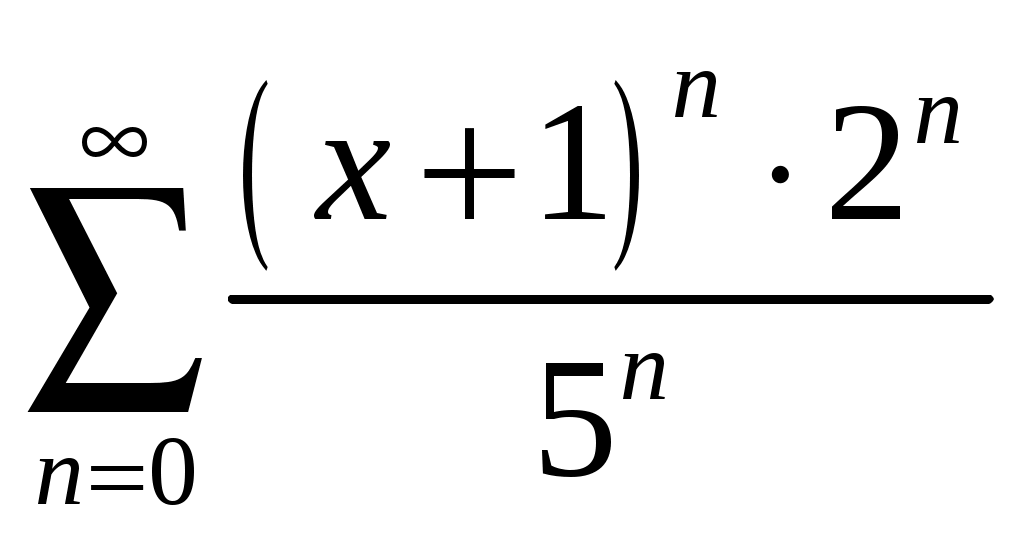 .
.Решение.
а) Найдем радиус сходимости по признаку Даламбера
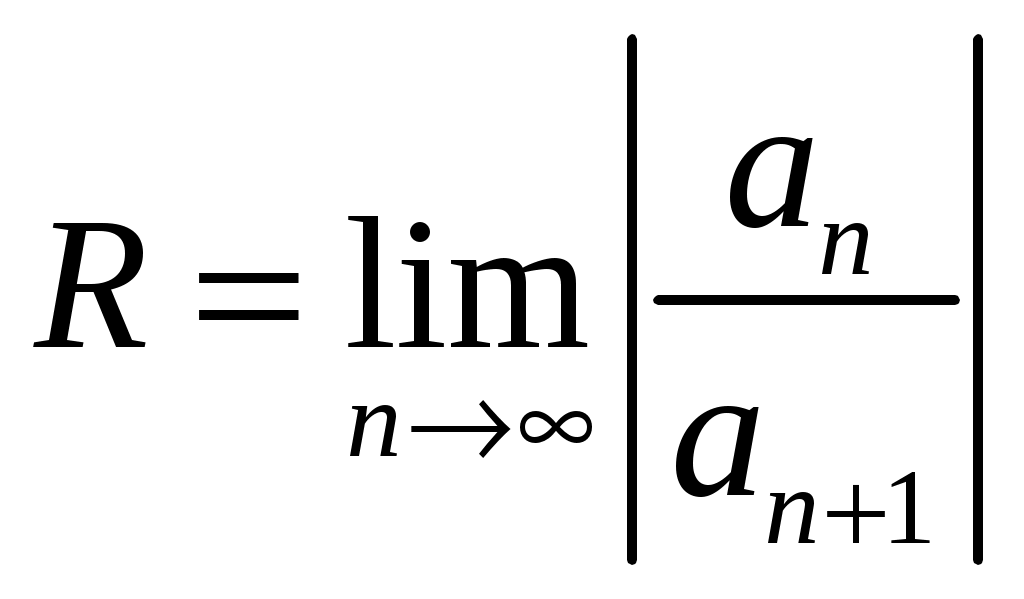 . Для данного ряда
. Для данного ряда , тогда получим:
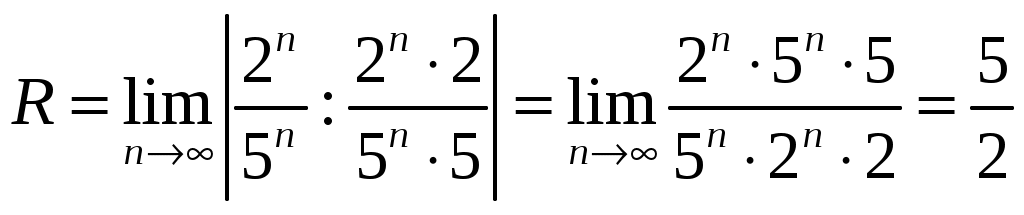 .
.Радиус сходимости ряда
1) Пусть
Исследуем на сходимость по признаку Лейбница. Проверив выполнений признака.
1)
Ряд
2) Пусть
Следовательно, исходный ряд сходится на интервале
б) Выпишем первые три члена ряда.
При
.
Тогда получим ряд
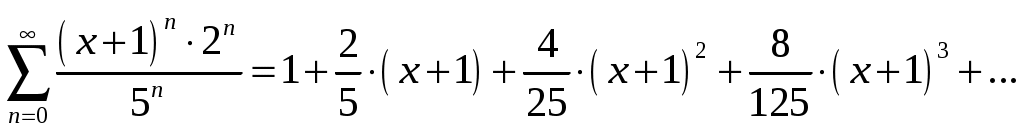 .
.Ответ: а) радиус сходимости
б)
Задача 72. Найти первые пять (ненулевых) членов разложения в степенной ряд решение ДУ с заданными начальными условиями:
Решение.
Так как начальные условия заданы в точке
Поскольку
Продифференцируем по
Продифференцируем по