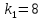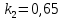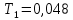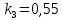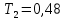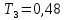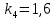Файл: Контрольная работа по дисциплине Основы теории управления.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 49
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»
(СПБГУТ)
ИНСТИТУТ НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ
(ИНО)
КОНТРОЛЬНАЯ РАБОТА
По дисциплине «Основы теории управления»
Вариант №7
Фамилия: Константинов
Имя: Василий
Отчество: Вольфович
№ зачетной книжки:
Группа №: ИБ-91з
Проверил: ___________
Санкт-Петербург
2021
Условие:
На рисунке представлена структурная схема одноконтурной системы управления, а в таблице 1 приведены параметры звеньев.
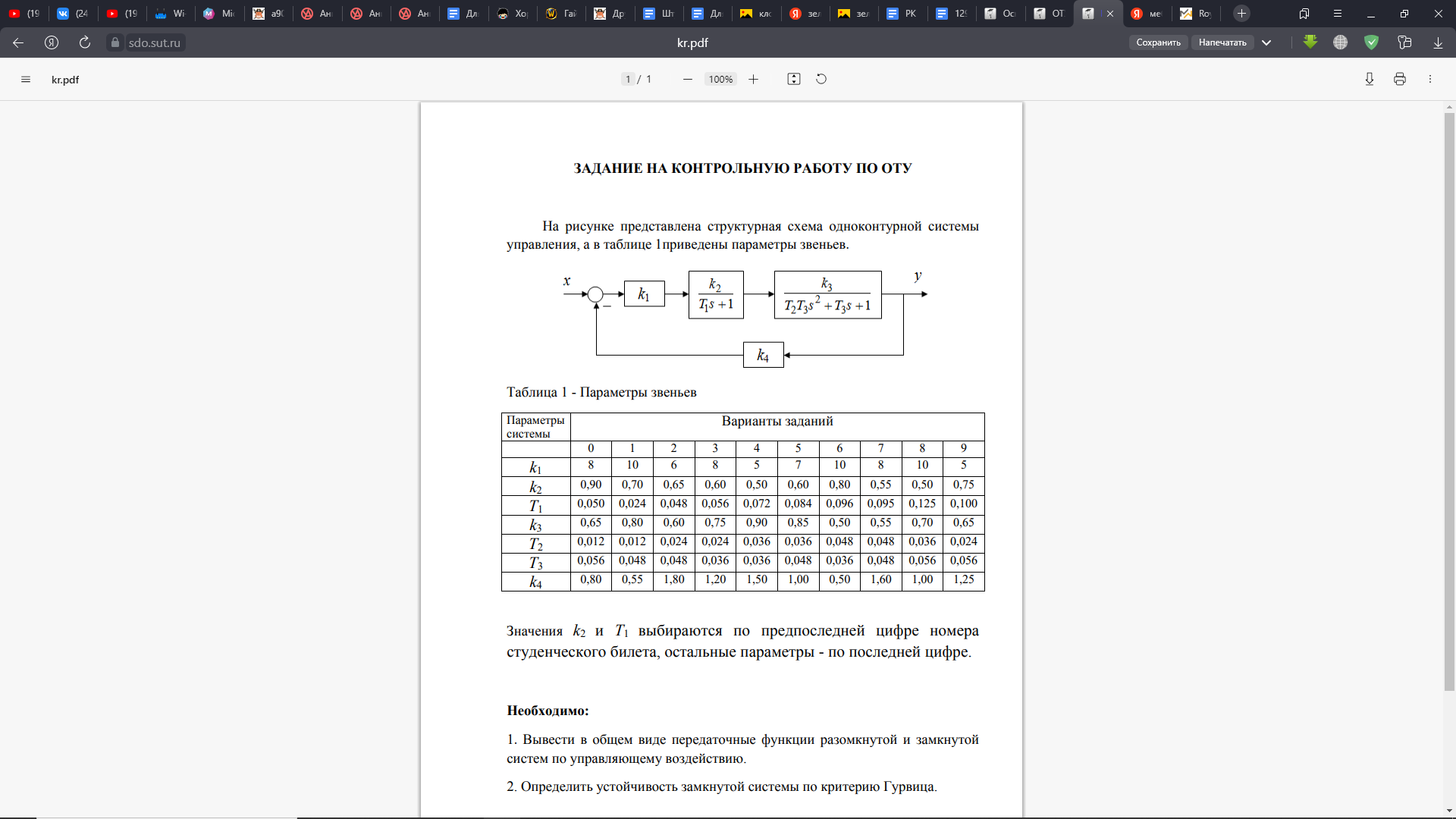
Таблица 1 – Параметры звеньев
Значения
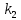и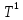 
выбираются по предпоследней цифре номера студенческого билета, остальные параметры – по последней цифре.Необходимо:
-
Вывести в общем виде передаточные функции разомкнутой и замкнутой систем по управляющему воздействию -
Определить устойчивость замкнутой системы по критерию Гурвица
Ход работы:
Значение для варианта №7:
-
Структурная схема является замкнутой системой с отрицательной обратной связью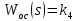
. Нам следует провести расчет передаточной функции разомкнутой системы и передаточной функции замкнутой системы с отрицательной обратной связью.
Передаточная функция последовательно соединенных звеньев равна произведению передаточных функций звеньев. Следовательно, передаточная функция разомкнутой системы выглядит так:
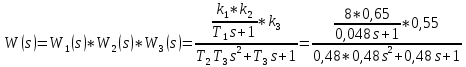
Передаточная функция замкнутой системы с отрицательной обратной связью, будет выглядеть вот так:
-
Устойчивость замкнутой системы по критерию Гурвица, определяется с помощью следующего способа:
-
Составляется характеристическое уравнение -
Условие устойчивости: необходимо и достаточно, чтобы n главных диагональных миноров определителя Гурвица были положительны, при условии, что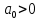
Характеристическое уравнение:
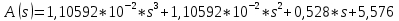
В итоге у нас получилось уравнение третьего порядка, имеющее вид:
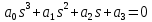, значит для этого используется частный случай критерия устойчивости для системы третьего порядка:Критерий устойчивости:
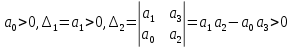
Далее проверяем критерий устойчивости:
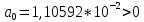
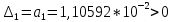
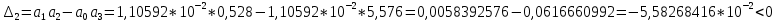
Критерий не выполнен, а это означает, что данная замкнутая система не является устойчивой.
Вывод
-
Были выведены в общем виде передаточные функции:
-
Разомкнутой системы: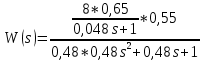
-
Замкнутой системы:
-
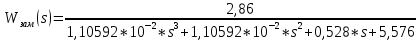
Замкнутая система по управляющему воздействию не является устойчивой по критерию Гурвица (для проверки устойчивости, использовался частный случай критерия для характеристического уравнения третьего порядка)