ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 66
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
а; ).
4) Решить неравенство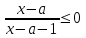
▼ Рассмотрим функцию f(x) =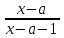
ОДЗ: х а + 1
Нули функции f(x): х - а = 0, х = а
Воспользуемся методом интервалов. Точки а и а + 1 разбивают ось на интервалы, на каждом из которых функция сохраняет знак.
При всех а число а + 1 > a, поэтому получаем следующее расположение этих точек на числовой оси:
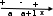
Отв. ха; а + 1 при любом а.
5) Решить неравенство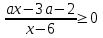
▼ Рассмотрим функцию f(x) =
ОДЗ: х 6
Коэффициент а при х в числителе может быть больше нуля, равен 0 и меньше 0.
Пусть а > 0, тогда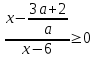
. Воспользуемся методом интервалов. Точки 
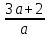и 6 разбивают ось на интервалы, на каждом из которых функция сохраняет знак. Так как определить порядок расположения этих точек на числовой оси однозначно нельзя, рассмотрим возможные случаи:
а)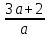 < 6, а > 2/3 х(-: 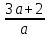(6; )
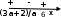
б)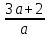 = 6, а = 2/3 х(-: 6)(6; )
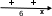
в)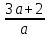 > 6, 0 < a < 2/3 х(-: 6) ; )
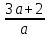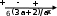
Пусть а = 0, тогда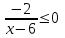
, x < 6, х(-: 6)
Пусть а < 0, тогда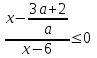
. Возможен только случай
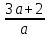< 6, а < 0 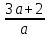; 6)
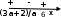
Отв. при а < 0, 
; 6); при 0 < a < 2/3, х(-: 6) ; );
при а = 2/3, х(-: 6)(6; ); а > 2/3, х(-: (6; ).
7) Решить неравенство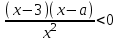
▼ Рассмотрим функцию f(x) =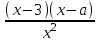
ОДЗ: х 0
Нули функции f(x): х = 3, х = а
Воспользуемся методом интервалов. Точки а, и 0 и 3 разбивают ось на интервалы, на каждом из которых функция сохраняет знак. Так как определить порядок расположения этих точек на числовой оси однозначно нельзя, рассмотрим возможные случаи:
а) при а < 0, х(а; 0)(0; 3).
б) при а = 0, х(0; 3).
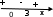
в) при 0 < а < 3, х(a; 3).
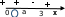
г) при а = 3 нет решений
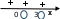
д) при а > 3, х(3: а)
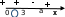
Отв. при а < -3/2, х(3: -2а); при а = -3/2 нет решений; при а > -3/2, х(-2а; 3)
4) Решить неравенство
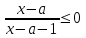
▼ Рассмотрим функцию f(x) =
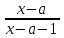
ОДЗ: х а + 1
Нули функции f(x): х - а = 0, х = а
Воспользуемся методом интервалов. Точки а и а + 1 разбивают ось на интервалы, на каждом из которых функция сохраняет знак.
При всех а число а + 1 > a, поэтому получаем следующее расположение этих точек на числовой оси:
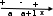
Отв. ха; а + 1 при любом а.
5) Решить неравенство
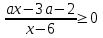
▼ Рассмотрим функцию f(x) =
ОДЗ: х 6
Коэффициент а при х в числителе может быть больше нуля, равен 0 и меньше 0.
Пусть а > 0, тогда
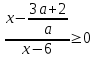. Воспользуемся методом интервалов. Точки 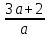и 6 разбивают ось на интервалы, на каждом из которых функция сохраняет знак. Так как определить порядок расположения этих точек на числовой оси однозначно нельзя, рассмотрим возможные случаи:а)
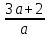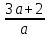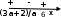
< 6, а > 2/3 х(-: (6; ) б)
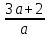= 6, а = 2/3 х(-: 6)(6; )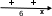 в)
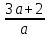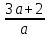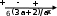
> 6, 0 < a < 2/3 х(-: 6) ; ) Пусть а = 0, тогда
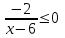, x < 6, х(-: 6)Пусть а < 0, тогда
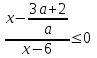. Возможен только случай 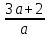< 6, а < 0 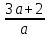; 6)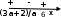 Отв. при а < 0,
; 6); при 0 < a < 2/3, х(-: 6) ; );при а = 2/3, х(-: 6)(6; ); а > 2/3, х(-:
(6; ).7) Решить неравенство
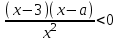
▼ Рассмотрим функцию f(x) =
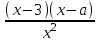
ОДЗ: х 0
Нули функции f(x): х = 3, х = а
Воспользуемся методом интервалов. Точки а, и 0 и 3 разбивают ось на интервалы, на каждом из которых функция сохраняет знак. Так как определить порядок расположения этих точек на числовой оси однозначно нельзя, рассмотрим возможные случаи:
а) при а < 0, х(а; 0)(0; 3).
б) при а = 0, х(0; 3).
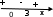
в) при 0 < а < 3, х(a; 3).
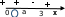
г) при а = 3 нет решений
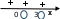
д) при а > 3, х(3: а)
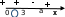
Отв. при а < -3/2, х(3: -2а); при а = -3/2 нет решений; при а > -3/2, х(-2а; 3)