Файл: Министервтсво цифрового развития, связи и массовых коммуникаций российской федерации.docx

Метод SVD

Метод главных компонент тесно связан с другим методом – разложением по сингулярным значениямSVD (Singular Value Decomposition). В этом случае исходная матрица X разлагается в произведение трех матриц (рис. 3): 



матрицы U и V – ортогональные, S - диагональная, значения на ее диагонали

называются сингулярными значениями σ₁ ≥ ... ≥ σ_R ≥ 0, которые равны квадратным корням из собственных значений λ_r:



Такое разложение обладает особенностью: если в матрице S оставить только k наибольших сингулярных значений, а в матрицах U и V только соответствующие этим значениям столбцы, то произведение получившихся матриц будет наилучшим приближением исходной матрицы X к матрице меньшего ранга k.


Рис. 3. Разложение матрицы Х по сингулярным значениям

Связь между PCA и SVD определяется двумя простыми соотношениями: 

и

2.2. Описание используемых библиотечных функций с примерами

Решение поставленной задачи будет выполнятьсяв среде RStudio, поэтому можно рассмотреть пример используемых библиотечных функций в нём (листинг 1). Для работы с jpg форматом воспользуемся библиотекой jpeg(строка2), позволяющей, в частности читать (функция readJPEG) и визуализировать (функция rasterImage) изображения. Для перевода цветного изображения в черно-белое используем библиотеку biOps(строка 3). В настоящее время эта библиотека исключена из репозитория CRAN и там дается только ссылка на архив, где она хранится. Изучив архив по этой ссылке, можно установить библиотеку с помощью следующей команды:

install.packages(path_to_file, repos = NULL, type="source"),

где path_to_file - путь к архивированному файлу.

После чтения и перевода в черно-белое представление нужно визуализировать оригинал изображения (строка 9, 10). Далее нужно определить размерность исходного изображения (dim(X) = 500 x 473) для дальнейшей оценки эффективности сжатия (строка 12). В конце находим сингулярное разложение X.svd(строка 14).

Листинг 1.

---

Использование метода главных компонент для понижения размерности



Сингулярное разложение X.svd представлено в виде списка (Largelist), состоящего из трех матриц, параметры которых можно посмотреть в закладе Environment правой верхней панелиRStudioи на рис. 4.



Рис. 4. Сингулярное разложение X.svd

Как видно из рис. 4, диагональная матрица S имеет размер 473 х 473, матрица U размер 500 х 473 и матрица V размер 473 х 473.

Матрицы S, U и V будут использоваться как основа из которой можно выбирать разное число главных компонент k. Формируем различные матрицы X_k, формирование проведем в цикле (строки 22-31 листинга 1) для числа компонент k = 5, 20, 50 и 250.

Сначала нужно сформировать усеченные матрицы Uk, Vk и Sk (строки 23–25). Затем в строке 26 выполним умножение сформированных матриц (см. рис. 3) для формирования сжатых изображений. Результатом работы этой программы будет четыре изображения, отличающихся по качеству (рис. 5):



Рис. 5. Изображения для k = 5, 20, 50, 250, соответственно

Можно предположить, что допустимым качеством обладает изображение для k = 50 сингулярных значений. Посмотрим, какой выигрыш можно получить, используя его вместо оригинала.



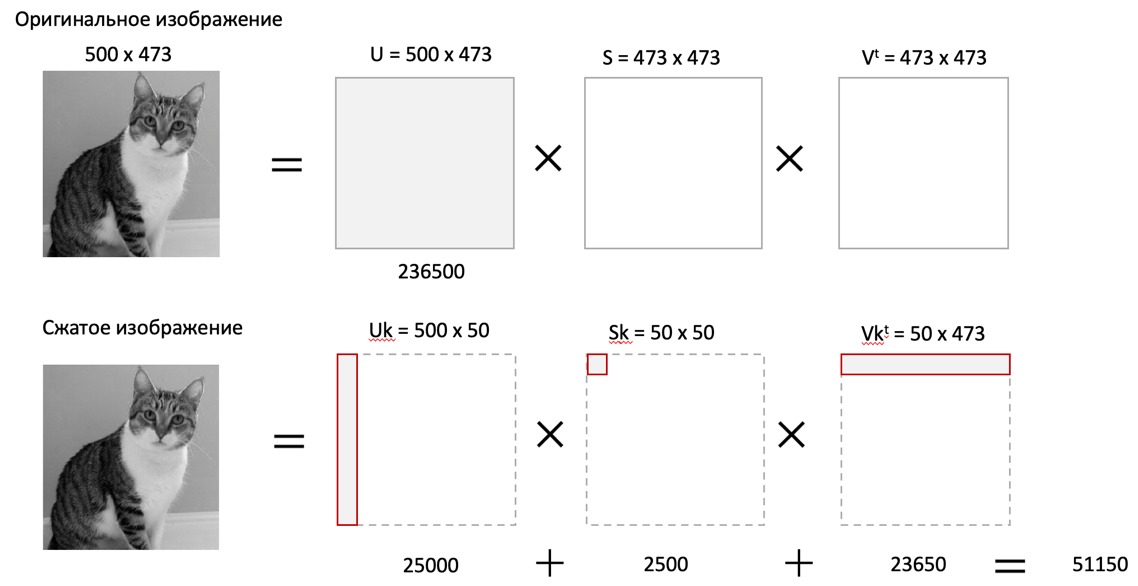
Рис. 6. Сравнение размерностей оригинального и сжатого изображения

На рис. 6 приведено такое сравнение, где показано, что вместо 236500 пикселей потребуется всего 51150, то есть выигрыш составляет 4,6 раза.

Для оценки количества информации, которое потеряется, заменив оригинальное изображение на сжатое, можно поступить следующим образом. Если суммарное количество значений всех главных компонент принять за 100% информационного наполнения оригинала, то сумма значений k главных компонент сжатого изображения определит его информационное наполнение. Разность вычисленных таким образом величин и даст оценку «потерянной»

3. Решение

3.1. Программный код с подробными комментариями

Листинг 2.

---

Производим установку требуемых для решения задачи библиотек – (строка 1, 2). Далее нужно подключить эти библиотеки (строка 4, 5).Потом считать одно из подготовленныхизображений (строка 9). После нужно перевести в черно-белое представление и визуализировать оригинал изображения (строка 11 и 13 соответственно). Далее определить размерность исходного изображения (dim(X) = 400x 400) для дальнейшей оценки эффективности сжатия (строка 15). В конце найти сингулярное разложение X.svd(строка 19).

В этом случае полученное сингулярное разложение X.svd представлено в виде списка (Largelist), состоящего из трех матриц, параметры которых можно посмотреть в закладе Environment правой верхней панелиRStudio.(рис. 7)


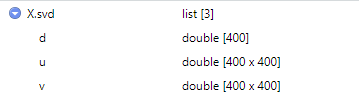
Рис. 7. Сингулярное разложение X.svd

Как видно из рис. 7, диагональная матрица S имеет размер 400 х 400 (и представлена как вектор d, в X.svd), матрица U размер 400 х 400 и матрица V размер 400 х 400.

Матрицы S, U и V будут использоваться как основа, из которой можно выбирать разное число главных компонент k. Нужно сформировать усеченные матрицы Uk, Vk и Sk (строки 26–28). Затем выполнить умножение сформированных матриц для формирования сжатых изображений (строка 29).

Нужно сформировать различные матрицы Xk: формирование будет проводиться,изменяя k(число компонент) до тех пор, пока результат не будеьоптимальным(чем меньше k, тем лучше). В результатерешения получается, чтоk = 150 даёт вполне удовлетворительные результаты при минимальности k(меньшееkуже не подойдет).

Далее нужно визуализировать результат с помощью функции image(), обработанной матрицы Xk (используем функции t() и apply(), чтобы повернуть изображение) и задания параметров цветокора (col = rgb(0:255,0:255,0:255,max=255)) в строке 31.

Далее (начиная со строки 33) делаем то же самое, но только используя матрицы метода PCA, т. к. связь между PCA и SVD определяется двумя простыми соотношениями:  и (строки 35–36). После этого нужно сформировать усеченные матрицы для метода PCA с тем же числом компонент (строки 38–40). Формируем матрицу Xk(строка 41).

Визуализируем результат с помощью функции image(), обработанной матрицы Xk (используем функции t() и apply(), чтобы повернуть изображение) и задания параметров растрирования (useRaster = TRUE) и цветокора (col = rgb(0:255,0:255,0:255,max=255)) в строке 43.

---

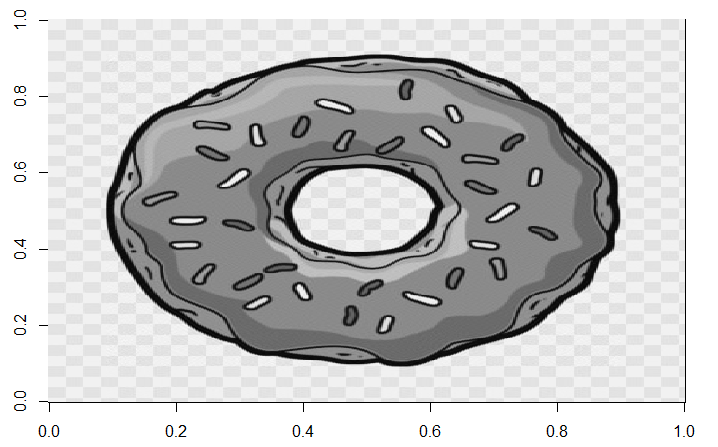
Рис. 8.Изображения для k = 100, 80, 120, 150 (слева направо, сверху вниз)соответственно (методом SVD)

3.2. Полученные результаты с выводами, пояснения полученных графических материалов

В результате выполнения программы с числом компонент равным 50, получаем следующие графические результаты методамиSVD и PCA (рис. 9)

Рис. 9. Изображения, полученные (k = 150) методом SVD (слева) и PCA (справа)


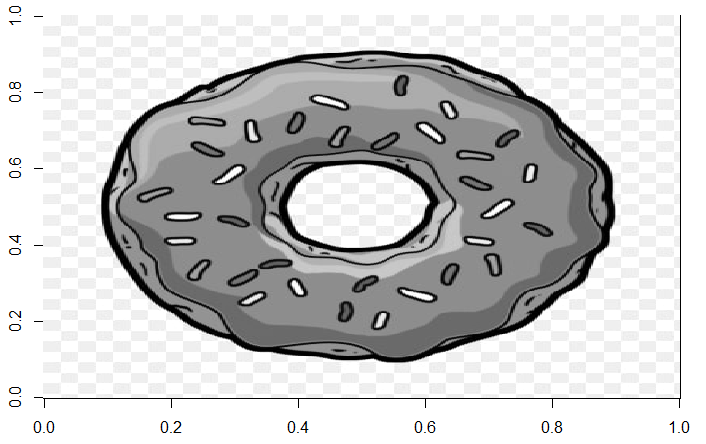
Рис. 10. Оригинал изображения в ч/б

Внешне глазом результаты неотличимы друг от друга, но результат выглядит более размыто в отличии от оригинала. То, что результаты сложно отличить, ответит то сколько информации сохранили сжатые изображения и сколько потеряли.

Метод SVD:



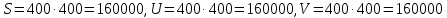
Тогда исходя из начального кол-во пикселей получаем:



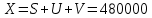
Для сжатого изображения:



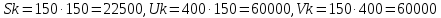
Тогда получаемкол-во сохраненной информации:







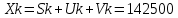
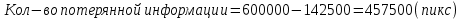
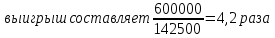
Метод PCA:



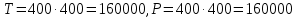
Тогда исходя из начального кол-во пикселей получаем:



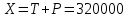
Для сжатого изображения:



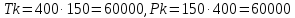
Тогда получаем кол-во сохраненной информации:

---

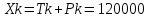
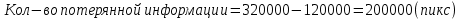
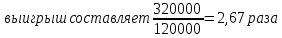
Исходя из подсчётов можно заметить, что сохранённая информация практически совпадает (различия малы), но есть значительные отличия в потерянной информации и соответственно в выигрыше при сжатии. Обусловлено это тем, что изначально мы храним различное кол-во информации (три матрицы в методе SVD и две матрицы в методе PCA).

Чтобы выяснить зависит ли достаточное число компонент для качественной визуализации от характера изображения, у нас есть изображение большего размера 920 х 920 px. Используя тот же код, обработаем его с числом компонент 150 (только методом SVD, т.к. поняли, что большой разницы между результатами PCAи SVDнет).

Рис. 11. Изображения, полученные методом SVD (k = 150 – слева), (k = 120 – справа)

Легко заметить, что при числе компонент в 120, изображение всё ещё нас не устраивает, оно слишком размытое. Но при том же числе в 150 все становится подходящим. Из этого делаем вывод, что при увеличении изображения, не нужно увеличивать кол-во компонент, по которым происходит сжатие. Если исходить из того, что данное изображение увеличилось примерно впятеро с 400х400pxдо 920х920px, а достаточное кол-во компонент, которое мы взяли, не изменилась, то зависимости кол-ва компонент от размера изначального изображенияне будет.


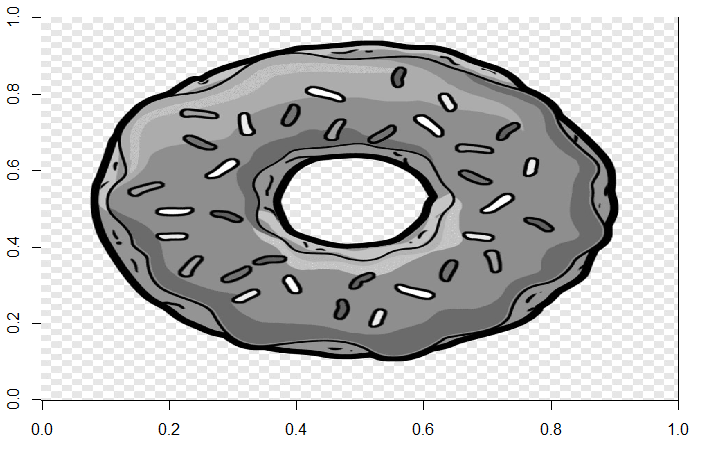
Рис. 12. Изображение, полученное методом SVD(k = 200 – слева) и оригинал в ч/б–справа

---