Файл: Министервтсво цифрового развития, связи и массовых коммуникаций российской федерации.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 238
Скачиваний: 10
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание № 2: Кластеризация данных
1.1. Задание на курсовую работу
Исследовать возможности классификации данных с использованием алгоритмов t-SNE и UMAP.
Исходные данные для анализа загрузить из ресурса WineQuality (http://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/) репозитория [1]. Варианты заданий (номер варианта определяется последней цифрой номера зачетки) приведены в табл. 2.
| Вариант | Обучающая выборка |
| Четная цифра | winequality-red.csv |
Таблица 2. Варианты задания
Анализируемые данные включают 11 объективных параметров различных сортов вина:
-
фиксированная кислотность; -
летучая кислотность; -
лимонная кислота; -
остаточный сахар; -
хлориды; -
свободный диоксид серы; -
общий диоксид серы; -
плотность; -
pH; -
сульфаты; -
спирт.
Последний, 12-й параметр является субъективной оценкой качества, проставляемой экспертом, и имеет несколько градаций.
Основная задача исследования состоит в определении качества субъективной оценки экспертов и формированию обоснованной кластеризации вин.
1.2. Загрузка и подготовка исходных данных для анализа
Исходные данные для анализа загружаем из ресурса WineQuality (http://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality-white.csv)
2. Основные сведения необходимые для выполнения курсовой работы
2.1. Главные теоретические положения лежащие в основе решения поставленной задачи
Алгоритм t-SNE
t-распределенное стохастическое соседнее вложение t-SNE (t-DistributedStochasticNeighborEmbedding) — это алгоритм нелинейного уменьшения размерности, используемый для исследования данных большой размерности. Он отображает многомерные данные в двух или более измерениях, подходящих для наблюдения человеком. Алгоритм t-SNE (2008), в ряде случаев намного эффективнее PCA (1933). Важно подчеркнуть, что большинство нелинейных методов, кроме t-SNE, не способны одновременно сохранять локальную и глобальную структуру данных [L.J.P. vanderMaatenandG.E. Hinton. Visualizing High-Dimensional Data Using t-SNE. Journal of Machine Learning Research 9(Nov):2579-2605, 2008].
SNE начинается с преобразования многомерной евклидовой дистанции между точками в условные вероятности, отражающие сходство точек. Математически это выглядит следующим образом:
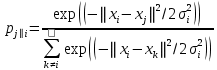
Формула показывает, насколько точка xj близка к точке xi при гауссовом распределении вокруг xiс заданным отклонением σ. Сигма будет различной для каждой точки. Она выбирается так, чтобы точки в областях с большей плотностью имели меньшую дисперсию. Для этого используется оценка перплексии (perplexity):
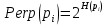 ,
,где
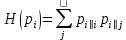
- энтропия Шеннона.
Перплексия может быть интерпретирована как сглаженная оценка эффективного количества «соседей» для точки xi. Она задается в качестве параметра метода t-SNE и рекомендуется использовать ее значение в интервале от 5 до 50. Сигма определяется для каждой пары xi и xj при помощи алгоритма бинарного поиска.
Таким образом, t-SNE алгоритм нелинейного уменьшения размерности, находит закономерности в данных, идентифицируя наблюдаемые кластеры на основе сходства точек данных с несколькими функциями. Но это не алгоритм кластеризации, а алгоритм уменьшения размерности, который просто отображает многомерные данные в более низкоразмерное пространство, а не идентифицирует входные объекты. Таким образом, вы не можете делать никаких выводов, основываясь только на t-SNE. По сути, это в основном техника исследования и визуализации данных. Но алгоритм t-SNE можно использовать в процессе классификации и кластеризации, используя его выходные данные в качестве входных характеристик для других алгоритмов классификации.
Алгоритм t-SNE можно использовать практически для всех многомерных наборов данных. Он особенно широко применяется в обработке изображений, естественного языка и геномных данных.
Ниже приведены распространенные ошибки, которых следует избегать при интерпретации результатов анализа с использованием алгоритма t-SNE:
-
Чтобы алгоритм работал правильно перплексия должнанаходиться в диапазоне от 5 до 50 и должна быть меньше количества переменных. -
Размеры кластеров на любом графике t-SNE не должны оцениваться на предмет стандартного отклонения, дисперсии или любых других аналогичных показателей. Это связано с тем, что t-SNE расширяет более плотные кластеры и сжимает более разреженные кластеры для выравнивания размеров кластеров. Это одна из причин получения четких и ясных графиков. -
Расстояния между кластерами могут измениться, потому что глобальная геометрия тесно связана с оптимальной сложностью. А в наборе данных с множеством кластеров с разным количеством элементов одна перплексия не может оптимизировать расстояния для всех кластеров. -
Шаблоны также могут быть обнаружены в случайном шуме, поэтому необходимо проверить несколько запусков алгоритма с разными наборами гиперпараметров, прежде чем решать, существует ли шаблон в данных. -
Различные формы кластеров могут наблюдаться на разных уровнях сложности. -
Топология не может быть проанализирована на основе одного графика t-SNE, перед проведением какой-либо оценки необходимо наблюдать несколько графиков.
Алгоритм UMAP
Аппроксимация и проекция однородного многообразия UMAP (UniformManifoldApproximationandProjection) — это метод уменьшения размерности, который можно использовать для визуализации аналогично t-SNE, но также для общего нелинейного уменьшения размерности. Алгоритм основан на трех предположениях о данных:
-
данные равномерно распределены на римановом многообразии; -
метрика Римана локально постоянна (или может быть аппроксимирована как таковая); -
многообразие локально связно.
Исходя из этих предположений, можно смоделировать многообразие с нечеткой топологической структурой. Вложение находится путем поиска низкоразмерной проекции данных, которая имеет наиболее близкую возможную эквивалентную нечеткую топологическую структуру.
Подробности лежащей в основе математики можно найти у авторов этого алгоритма в [https://arxiv.org/pdf/1802.03426.pdf ].
UMAP — это новый алгоритм уменьшения размерности, библиотека с реализацией которого вышла совсем недавно. Авторы алгоритма считают, что UMAP способен бросить вызов современным моделям снижения размерности, в частности, t-SNE, который на сегодняшний день является наиболее популярным. По результатам их исследований, у UMAP нет ограничений на размерность исходного пространства признаков, которое необходимо уменьшить, он намного быстрее и более вычислительно эффективен, чем t-SNE, а также лучше справляется с задачей переноса глобальной структуры данных в новое, уменьшенное пространство.
2.2. Описание используемых библиотечных функций с примерами
Пример использования алгоритма t-SNE
Ниже представлен пример использования алгоритма t-SNE для анализа набора данных MNIST и сравним его возможности с результатом, полученным ранее с использованием метода РСА (листинг 3):
Листинг 3. Анализ MNIST методами PCA и t-SNE
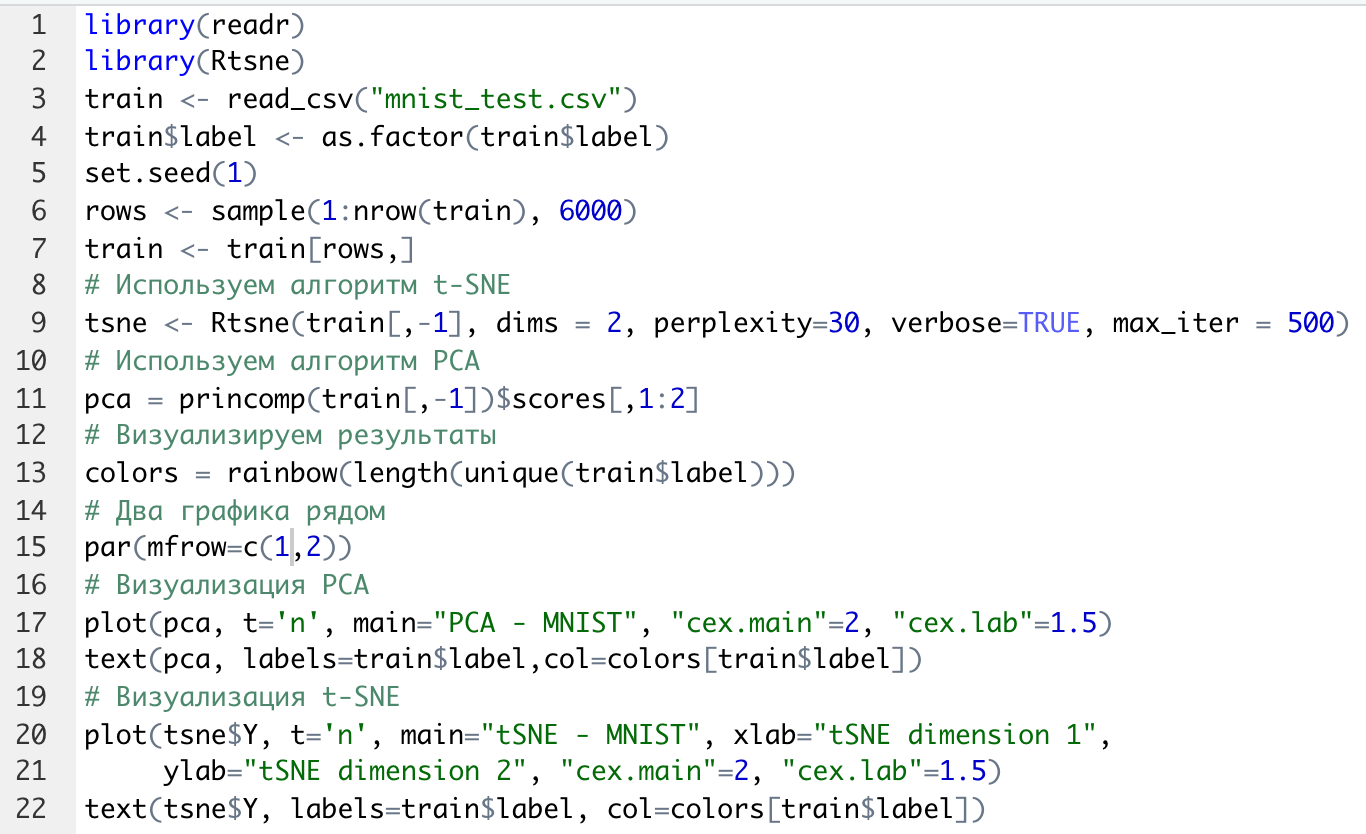
В листинг 3 добавлена функция Rtsne (строка 9) для реализации алгоритма t-SNE. Она имеет много входных параметров для настройки.
В строке 15 параметр par(mflow= c(1,2)) определяет вывод двух графиков рядом в оной строке. В результате мы получим следующую визуализацию (рис. 13).
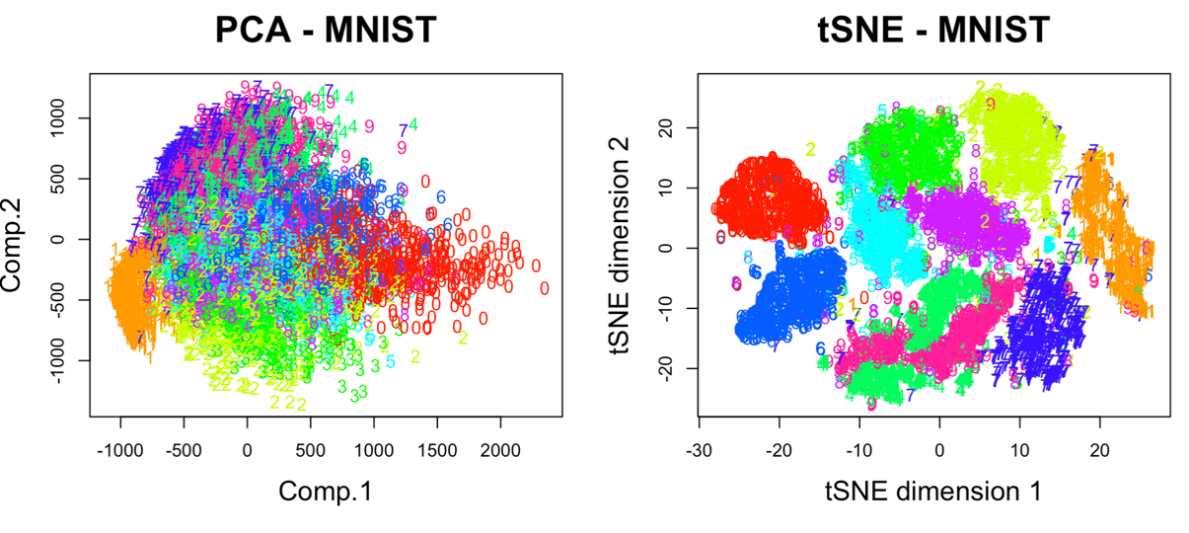
Рис. 13. Визуализация MNIST по двум компонентам с использованием PCA и tSNE
Пример использования алгоритма UMAP
Ниже представлен пример использования алгоритма UMAP (листинг 5) для анализа набора данных MNIST и сравним его возможности с результатом, полученным ранее с использованием методов РСА и t-SNE в листинге 3.
Код листинга 4 максимально идентичен коду листинга 3, с той лишь разницей, что здесь используется функция umap().
Листинг 4. Анализ MNIST методом UMAP
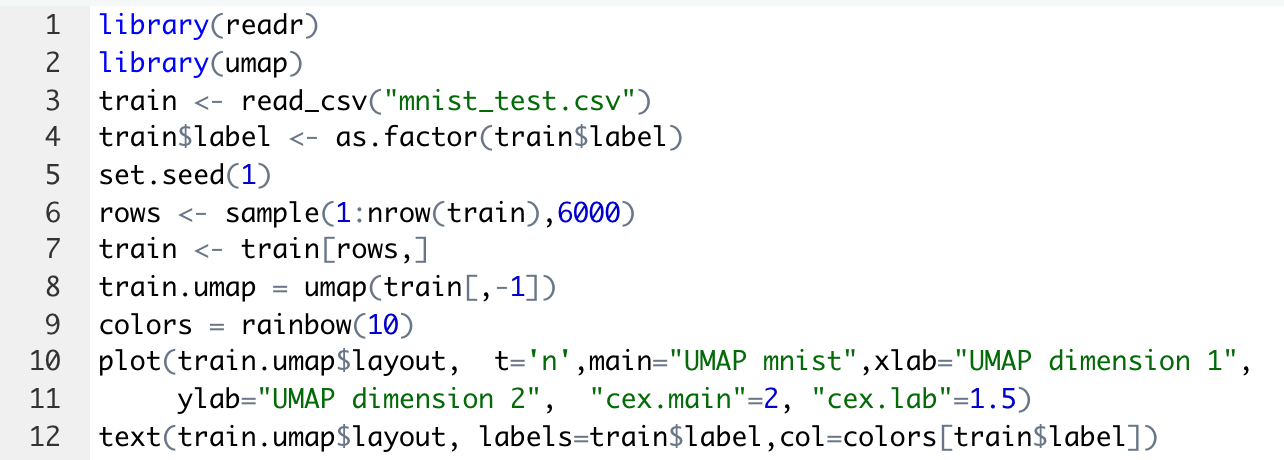
В результате получается следующую визуализацию (рис. 14), которая показывает потенциальные возможности классификации набора.
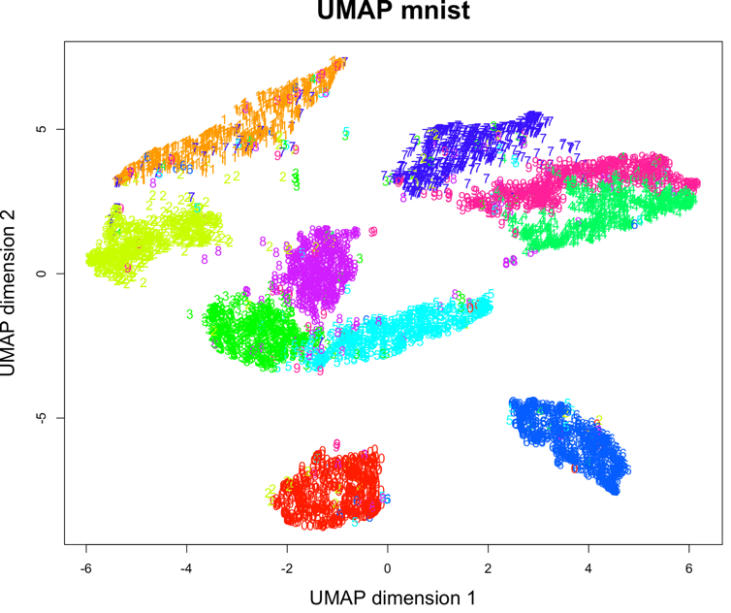
Рис. 14. Визуализация MNIST по двум компонентам с использованием UMAP
3. Решение
3.1. Программный код с подробными комментариями
Листинг 5.
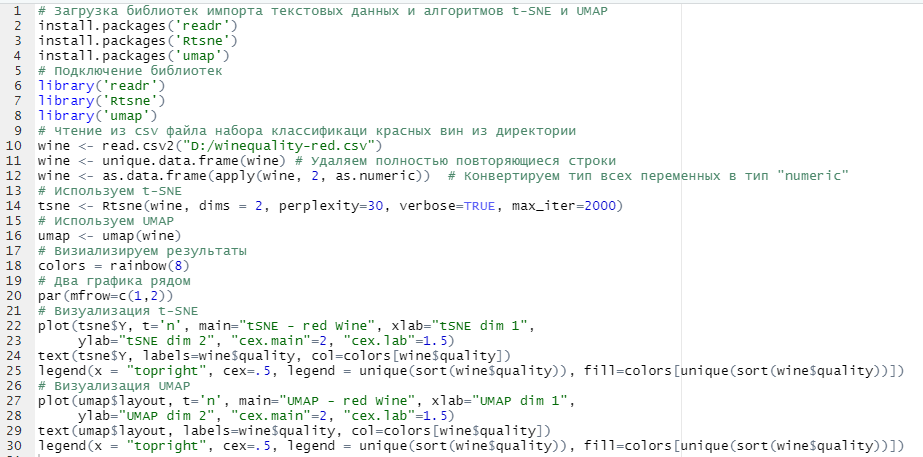
Сначала нужно загрузить необходимые для работы библиотеки: импорта данных, алгоритмов t-SNEиUMAP (строки 2–3). Подключаем их (строки 6–7). После этого нужно считать файл с исходными данными в формате .csv и получаем data.frame (строка 10). Потом необходимо удалить повторяющиеся строки из data.frame и конвертируем все переменные в numeric, т.к. иначе ф-иUMAP и Rtsne не сработают (строки 11–12). На этом заканчивается подготовка данных. После этого нужно применить функции алгоритмов t-SNEи UMAP (строки 15 и 17). Последующий код отвечает за построение графиков на основании полученных данных:
-
colorsотвечает за палитру графиков; -
par(mfrow=c(1,2)) позволяет расположить два графика рядом; -
plot()строит координатную плоскость с заданными параметрами осей, подписей и масштабирования (t='n', поэтому именно плоскость без данных); -
text() отображает данные в виде цифр (его параметры задают каким цветом они отобразятся) -
legend() позволяет добавить к графику легенду, чтобы лучше ориентироваться в данных
3.2. Полученные результаты с выводами, пояснения полученных графических материалов