Файл: Министервтсво цифрового развития, связи и массовых коммуникаций российской федерации.docx

МИНИСТЕРВТСВО ЦИФРОВОГО РАЗВИТИЯ,

СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

Факультет Информационных систем и технологий

Кафедра Информационных Управляющих Систем


Технологии проектирования программного обеспечения информационных систем


Пояснительная записка к курсовой работе

Выполнил:

студент гр. ИБ-94з Экажев И.А.

Санкт-Петербург

2023

СОДЕРЖАНИЕ

ВВЕДЕНИЕ

Информация, которую мы получаем извне, как правило, из сети Интернет, может существовать во многих формах. Она может быть в графическом виде, в виде текста, таблиц, видео или аудио. Также иногда информация предстаёт в виде набора статистических данных, полученных в результате исследования. Для того, чтобы извлечь из этого хаоса какие-либо выводы, либо, изменить конечное представление информации, нужно уметь её обрабатывать. Для этого существуют алгоритмы обработки информации, каждый из которых служит конечной цели. Когда человек имеет дело с большими объёмами данных, это становится особенно актуально.

Язык R имеет множество библиотек, которые созданы и развиваются именно для того, чтобы обрабатывать данные (в т.ч. графические). В данной курсовой работе будет на простых примерах разобрана работа некоторых представленных в библиотеках языка R алгоритмах обработки информации. Также с помощью векторной графики будет визуализирован отрывок из сказки Чуковского.

---

Задание № 1: Понижение размерности данных

1.1.Задание на курсовую работу

Исследовать эффективность методов PCA и SVD для понижения размерности данных.

В качестве исходных данных для анализа следует самостоятельно выбрать изображение в формате jpg. Размер изображения должен быть не менее 400 х 400 пикселей.

В ходе исследования необходимо проделать следующее:

• 
  выбрать и обосновать количество главных компонент, достаточное для качественной визуализации;
  
• 
  оценить выигрыш сжатого изображения по объему, по сравнению с оригиналом;
  
• 
  оценить количество «утраченной» информации;
  
• 
  выяснить зависит ли достаточное число компонент для качественной визуализации от характера изображения (если да, то оценить эту зависимость).
  

1.2. Загрузка и подготовка исходных данных для анализа

В качестве исходных данных для анализа выберем следующее изображение, подходящее под условия: форма – jpg, размер – не менее 400x 400 пикселей(рис. 1).




Рис.1. Исходные изображение для выполнения задания(400х400 и 920х920)

2. Основные сведения необходимые для выполнения курсовой работы

2.1. Главные теоретические положения лежащие в основе решения поставленной задачи

Метод PCA

Методы понижения размерности играют важную роль в задачах обработки данных. Они позволяют строить модели в пространствах меньшей размерности, чем исходное признаковое пространство, с минимальными потерями информации. В ряде случаев полезно понижать размерность до двух, то есть проецировать данные на плоскость. Таким образом можно изучить структуру данных, например, посмотреть, насколько разделимы классы в задачах классификации.

---

Метод главных компонент PCA (PrincipalComponentAnalysis)— один из основных способов уменьшить размерность данных, с потерей наименьшего количества информации. В совокупности основная цель анализа главных компонентов заключается в следующем:

• 
  выявить скрытый паттерн в наборе данных,
  
• 
  уменьшить размерность данных за счет устранения шума и
  

избыточности,

• 
  определить коррелированные переменные.
  

Метод главных компонент применяется к данным, записанным в виде матрицы  X – прямоугольной таблицы чисел. Традиционно строки этой матрицы называются образцами, а столбцы – переменными (атрибутами). Цель – извлечение из этих данных нужной информации. Шум и избыточность в данных обязательно проявляют себя через корреляционные связи между переменными.

Суть метода главных компонент – существенное понижение размерности данных. Исходная матрица X заменяется двумя новыми матрицами T и P (рис. 1):

.

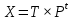Матрица T называется матрицей счетов (scores) , а матрица P — матрицей нагрузок (loadings). При этом, размерность матрицы Т, число ее столбцов k, меньше, чем число переменных m (столбцов) у исходной матрицы X.

---

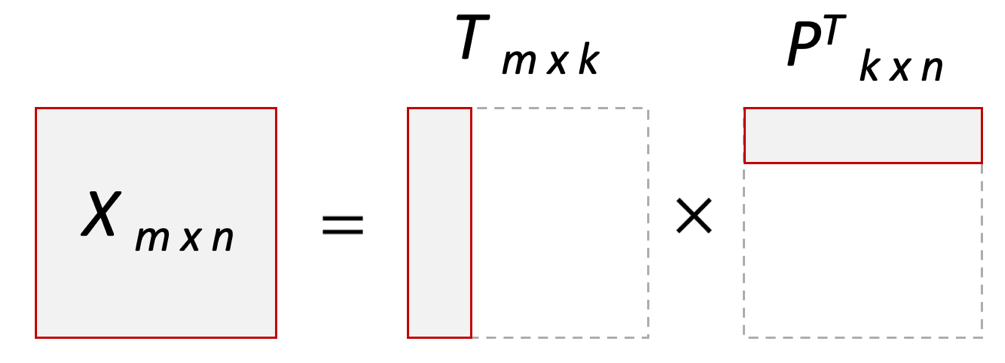
Рис. 1. Представление матрицы Х двумя матрицами Т и Р

Вторая размерность – число образцов (строк) сохраняется. Если декомпозиция выполнена правильно – размерность k выбрана верно, то матрица T несет в себе практически столько же информации, сколько ее было в начале, в матрице X. При этом матрицы T и P в совокупности меньше, и, стало быть, проще, чем X.

Метод главных компонент тесно связан с другим методом – разложением по сингулярным значениямSVD (Singular Value Decomposition). В этом случае исходная матрица X разлагается в произведение трех матриц (рис. 2): 



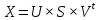
матрицы U и V – ортогональные, S - диагональная, значения на ее диагонали

называются сингулярными значениями σ₁ ≥ ... ≥ σ_R ≥ 0, которые равны квадратным корням из собственных значений λ_r:



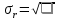
Такое разложение обладает особенностью: если в матрице

---

S оставить только k наибольших сингулярных значений, а в матрицах U и V только соответствующие этим значениям столбцы, то произведение получившихся матриц будет наилучшим приближением исходной матрицы X к матрице меньшего ранга k.



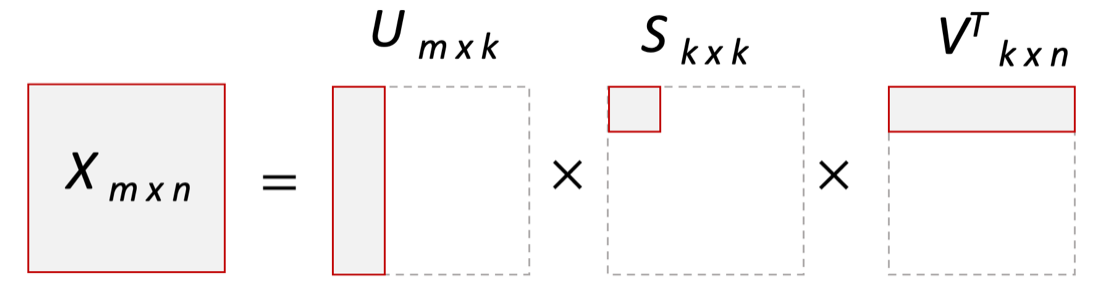
Рис. 2. Разложение матрицы Х по сингулярным значениям

Связь между PCA и SVD определяется двумя простыми соотношениям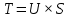и: 

и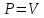

Таким образом, оба метода можно использовать для решения задач понижения размерности данных с минимальными потерями информации. При решении различных задач распознавания предполагается, что в наличии имеется некоторая выборка объектов, и для каждого объекта вычислен один и тот же набор признаков. На практике объекты могут быть представлены сложными многомерными данными, например, изображениями, набором кривых, текстом и так далее. Поэтому возникает задача извлечения из входных многомерных данных набора признаков, информативных с точки зрения дальнейшего решения задачи распознавания.

Любые многомерные данные всегда можно представить в виде вектора чисел. В случае изображений достаточно развернуть матрицу пикселей в вектор. Для текстов можно вычислить количество раз, которое встречается каждое слово в тексте, и сформировать вектор чисел, длина которого определяется общим числом слов в словаре. Подобные векторы чисел имеют, как правило, большую длину, а содержащиеся в них признаки, как правило, малоинформативны. Именно поэтому рассматривается задача сокращения размерности описания данных с целью получения относительно компактного множества информативных признаков.

---