Файл: Контрольная работа по теме Базы данных в Excel 72 IV. Макросы в ms excel 78 Макросы для автоматизации работ 78.doc

14.

A						Y
1	–5	1	2	–5		25
1	4	–4	–5	–5		–7
0	–5	–4	0	–3		15
1	–1	–1	0	–5		9
3	–4	4	4	–2		24

15.

A						Y
–3	4	2	–3	3		–18
1	2	–5	2	2		–33
–5	0	–1	–5	–4		–5
0	–2	–2	1	–1		1
0	0	4	–3	3		19

2.3. Задачи оптимизации

---

2.3.1. Общие сведения

Задачи оптимизации постоянно возникают в процессе деятельности современных организаций и предприятий. При этом типовыми задачами являются:

• 
  поставки сырья;
  
• 
  составление оптимальных планов выпуска продукции;
  
• 
  управление запасами;
  
• 
  распределение ресурсов;
  
• 
  планирования инвестиций;
  
• 
  составление рационов (смесей, сплавов);
  
• 
  назначения на должности;
  
• 
  оптимальная замена оборудования и т. д.
  

С подобными задачами в своей повседневной работе сталкиваются менеджеры, экономисты, финансисты, фермеры и др.

Модели всех задач на оптимизацию состоят из следующих элементов:

1. Независимые переменные – величины, которые нужно найти при решении задачи.

2. Целевая функция – зависимая величина, которая является целью, ключевым показателем эффективности или оптимальности модели.

3. Ограничения – условия, которым должны удовлетворять переменные.
2.3.2. Пример

При откорме каждое животное ежедневно должно получать не менее 20 единиц питательного вещества S₁, не менее 30 единиц вещества S₂, не менее 10 единиц S₃ и не менее 40 единиц S₄. Для составления рациона используют пять видов корма. Содержание количества единиц питательных веществ в 1 кг каждого вида корма и стоимость 1 кг корма каждого вида приведены в табл. 2.

Таблица 2

Питательные вещества	Количество единиц питательных веществ в 1 кг корма					Требуется не менее
	К1	К2	К3	К4	К5
S1	2	12	10	1	2	20
S2	12	0	0	4	3	30
S3	1	8	3	0	4	10
S4	2	2	4	6	2	40
Стоимость 1 кг корма (ден.ед)	12	36	32	18	10

---

Необходимо составить дневной рацион нужной питательности, причём затраты на него должны быть минимальными.

Для составления математической модели задачи обозначим через х_i, количество килограммов корма К_i в дневном рационе (i =1, 2,…,5). Принимая во внимание значения, приведённые в табл. 2, и условие, что дневной рацион удовлетворяет требуемой питательности только в случае, если количество единиц питательных веществ не меньше предусмотренного, получаем систему ограничений:

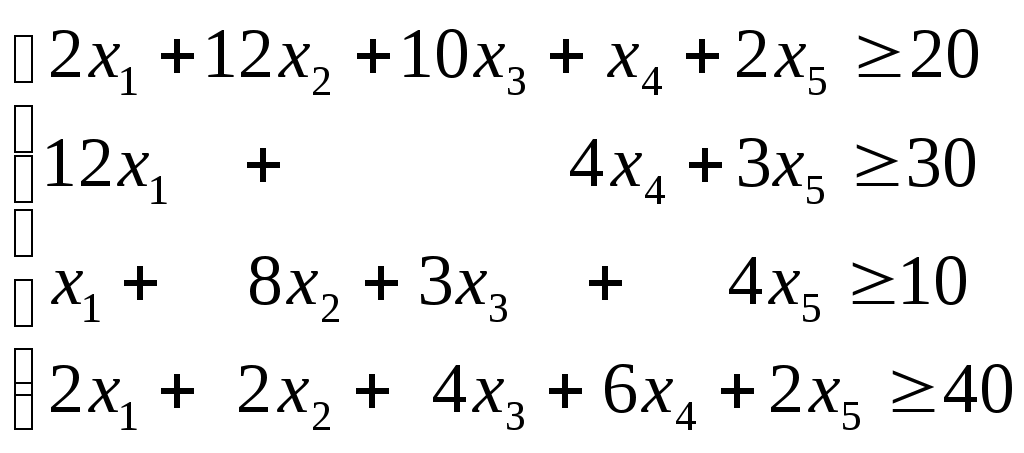. (4)

Очевидно, что должны выполняться условия неотрицательности неизвестных:

х_i , (i =1,…,5) (5)

Общую стоимость дневного рациона можно выразить в виде линейной функции

f= 12x₁+ 36x₂+32x₃+ 18x₄+10x₅. (6)

Таким образом, задача заключается в нахождении решения системы (4), удовлетворяющего условиям (5), при котором функция (6) принимает минимальное значение.
Рассмотрим этапы реализации данной задачи в MS Excel.

В Excel необходимо создать таблицу с формулами, которые связывают план, ограничения и целевую функцию Стоимость (рис. 2.2):


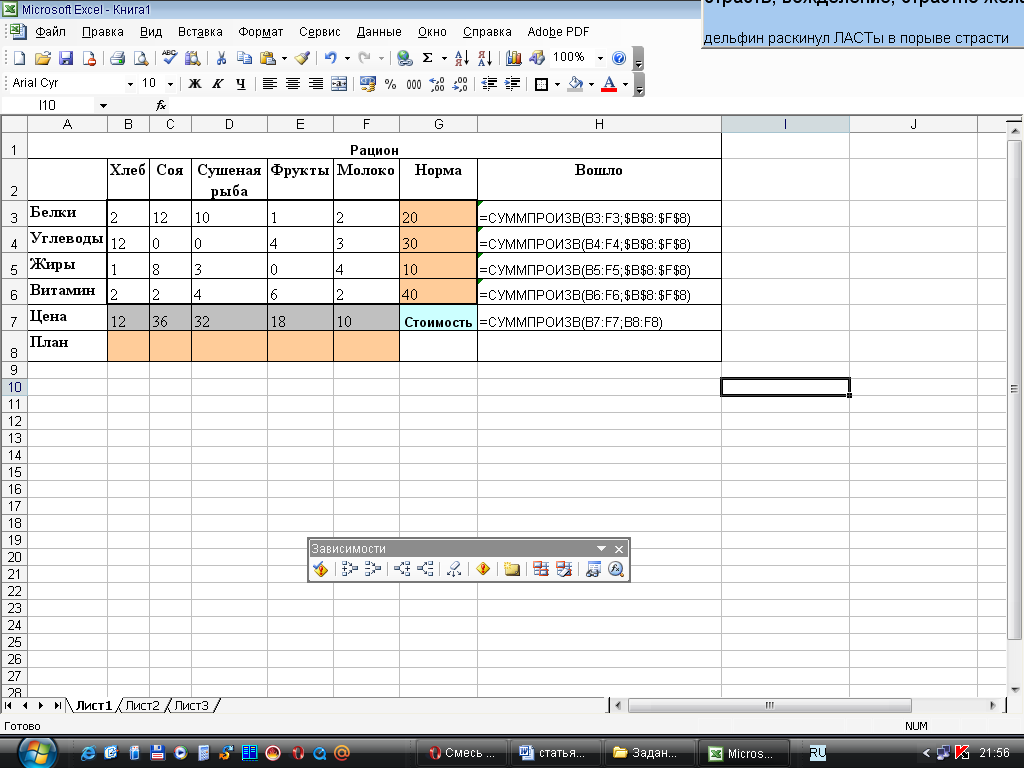
Рис. 2.2. Таблица с исходными данными и формульными зависимостями
Программа Поиск решений запускается командой:

Сервис > Поиск решения.

В полях Установить целевую ячейку, Изменяя ячейки, Ограничения вводятся соответствующие данные (рис. 2.3).



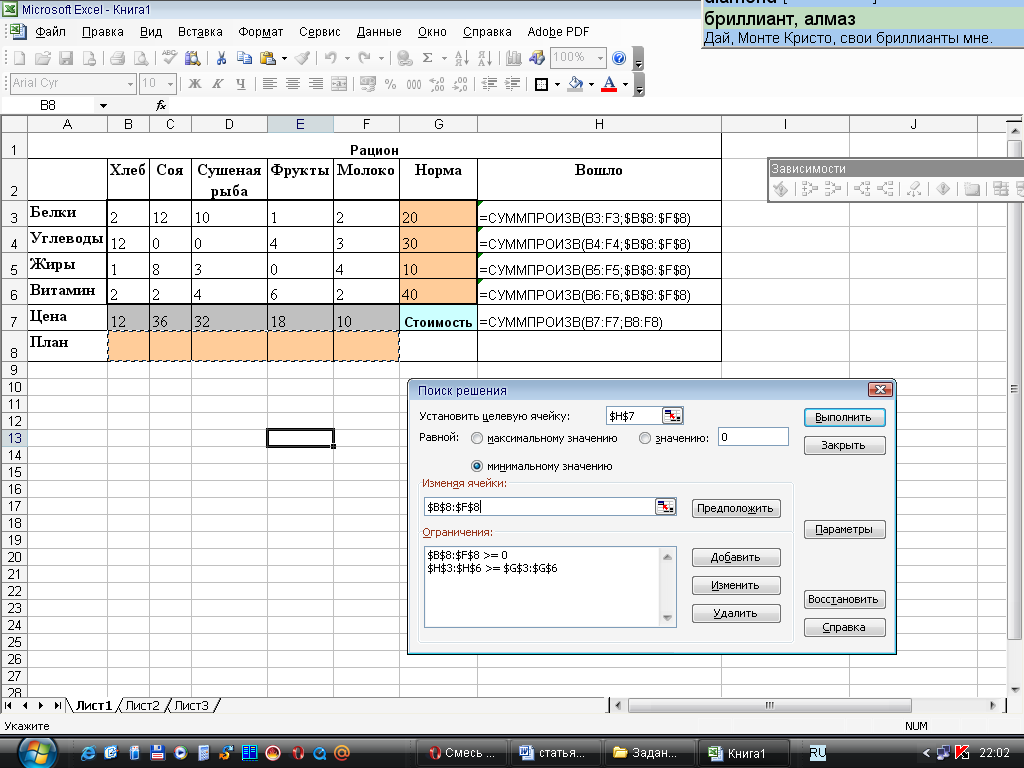
Рис. 2.3. Окно Поиск решения
Так как это линейная модель (целевая функция S является линейной), то необходимо установить в окне Параметры поиска решений переключатель в позицию Линейная модель. После нажатия на кнопку Выполнить в появившемся окне Результаты поиска решения укажите Отчет по устойчивости. Результаты поиска решения и полученный отчет представлены на рисунках 2.4 и 2.5.

---

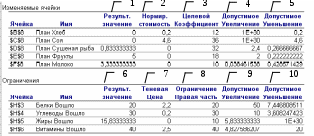
Рис. 2.5. Отчет по устойчивости
Отчет по устойчивости отражает чувствительность структуры полученного плана до изменений начальных данных и дальнейшие действия менеджера с целью улучшения результатов. Такой отчет не создается для моделей, значения в которых ограничены множеством целых чисел.

1. Результирующее значение – оптимальный план задачи.

В данной конкретной задаче оптимальный рацион минимальной стоимости 150 д. ед. состоит из 0,83 кг сушеной рыбы, 5 кг. фруктов и 3,33 л. молока.

2. Нормированная стоимость неизвестных плана указывает, как изменится стоимость рациона при желании добавить в его состав «невыгодный» продукт, например, единица хлеба в рационе увеличит его стоимость на 0,2 д. ед., единица сои – на 4,6 д. ед.

3. Коэффициенты целевой функции.

4, 5. Границы изменений значений коэффициентов целевой функции при условии, что количество оптимальной продукции (план) не изменится. Например, если целевой коэффициент Фруктов (КФ) равен 18 (цена за 1 кг. товара), то изменяя его в рамках 18-0,22<КФ<18+2, 17,78<КФ<20 план не изменится, но значения стоимости может уменьшиться или увеличиться.

6. Количество использованных ресурсов;

7. Теневые цены показывают уровень влияния значения норм (в сравнении с другими ресурсами) на стоимость рациона относительно ее увеличения. В данном примере нормы на состав витаминов более «влиятельные» на стоимость, чем белки (2,5>2,2).

Например, если увеличить норму витаминов на 1 единицу (до 41), то стоимость увеличится на 2,5 д. ед. и будет составлять 152,5 д. ед.

8. Нормы белков, жиров, углеводов и витаминов в дневном рационе. Соответствуют условию задачи.

9, 10. Задают диапазон для 8, в котором действует теневая цена 7 (аналогично 4, 5).
2.3.3. Варианты заданий

1. 
   Фирма производит три вида изделий – А, В и С. Для их выпуска требуется обработка на станках: I, II, III, IV. Время обработки на станках, а также прибыль от реализации изделия каждого вида приведены в таблице.
   

Изделие	Время обработки, ч				Прибыль, $
	I	II	III	IV
А	1	3	1	2	3
В	6	1	3	3	6
С	3	3	2	4	4

---

Составить план выпуска изделий дающий максимальную прибыль, если известно, что фонд рабочего времени станков соответственно равен 84, 42, 21 и 24 часа.

2. 
   Фирме для производства требуется уголь с содержанием фосфора не более 0.03% и с примесью пепла не более 3.25%. Доступны три сорта угля – А, В и С, параметры которых приведены в таблице.
   

Сорт угля	Содержание фосфора, %	Содержание пепла, %	Цена, $
А	0,06	2,0	30
В	0,04	4,0	30
С	0,02	3,0	40

Составить из указанных сортов такую смесь, чтобы она удовлетворяла требованиям производства по содержанию фосфора и пепла и имела минимальную цену.

3. 
   Фирма производит два продукта А и В, рынок сбыта которых неограничен. Каждый продукт должен быть обработан на машинах: I, II, III. Время обработки в часах для каждого из изделий А и В приведено в таблице.
   

	I	II	III
А	0,5	0,4	0,2
В	0,25	0,3	0,4

Недельный фонд рабочего времени машин I, II, III равен соответственно 40, 36 и 36 часам. Прибыль от изделий А и В составляет соответственно 5 и 3 доллара. Фирме надо определить недельные нормы выпуска изделий А и В, максимизирующие прибыль.

4. 
   На кондитерскую фабрику г. Ступино перед Новым годом поступили заказы на подарочные наборы конфет из трех мага­зинов. Возможные варианты наборов, их стоимость и оставши­еся товарные запасы на фабрике представлены в таблице.
   

Определить оптимальное количество подарочных наборов, которые фабрика может предложить магазинам и обеспечить максимальный доход от продажи.

Наименование конфет	Вес конфет в наборе, кг			Запасы конфет, кг
	А	В	С
«Сникерс»	0,3	0,2	0,4	600
«Марс»	0,2	0,3	0,2	700
«Баунти»	0,2	0,1	ОД	500
Цена, руб.	72	62	76

---