Файл: Контрольная работа по теме Базы данных в Excel 72 IV. Макросы в ms excel 78 Макросы для автоматизации работ 78.doc

---

II. Численные методы

1. 
   Решение алгебраических уравнений
   

2.1.1. Общие сведения

С помощью инструмента Подбор параметра в Excel можно решать уравнения вида

f(x) = C, (2.1)

где f(x) – непрерывная функция, а С ­– некоторая постоянная.

Применение этого инструмента можно разделить на два шага.

1. 
   Подготовить таблицу для вычисления f(x) с каким-либо начальным значением параметра x. При этом в ячейке, предназначенной для f(x), должна быть введена формула, содержащая ссылку на ячейку с параметромx(может быть и не напрямую, а опосредованно - через цепочку других ссылок). В ячейке, отведенной для параметраx, должно быть записано число.
   
2. 
   Вызвать окно инструмента Подбор параметра, заполнить его поля и после нажатия кнопки ОК система сама с приемлемой точностью найдет решение уравнения.
   

2.1.2. Пример

Цена на товар вначале увеличилась на 25%,а затем снизилась на 15%, после чего она стала равной 163 руб. Определить исходную цену товара.

Решение.

1. Подготовим в Excel таблицу для расчета итоговой цены, считая первоначальную цену известной и равной, например, 100 р.

	A	B
1	Исходная цена	100
2	Цена после повышения на 25%	=B1*1,25
3	Цена после снижения на 15%	=B2*0,85

В итоге в ячейке B3 получим значение, равное 106,25. Чтобы подобрать исходную цену, при которой итоговая цена станет равной 163 р. выполните

2. Выберите в меню Сервис команду Подбор параметра…


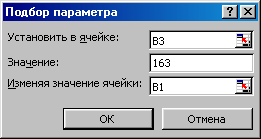
Рис.2.1. Окно Подбор параметра
В появившемся окне (рис.2.1) введите для поля Установить в ячейке

---

значение B3, для поля Значение – 163, для поля Изменяя значение ячейки – B1. После нажатия кнопки ОК Excel автоматически подберет значение ячейки B1, при которой в B3 получится результат, равный 163. Таким значением окажется цена 151,41 р.
2.1.3. Варианты заданий

1. Определить, какой должна быть оптовая цена товара, чтобы вместе с 16% торговой наценкой и с последующим 5% президентским налогом с продажи розничная цена равнялась 25 руб.
2. Банк ежемесячно начисляет проценты по формуле сложных процентов:

,

где S – текущий вклад;

P – начальный вклад;

c – сложная ставка;

t – время.

Определить, какой должна быть исходная сумма, чтобы через 6 месяцев при ставке 10% общая сумма вклада оказалась равной 2000 руб.
3. Банк ежемесячно начисляет проценты от суммы вклада. Определить, каким должна быть процентная ставка, чтобы через 6 месяцев при начальном вкладе, равном 1000 руб., на счете оказалась сумма, равная 2000 руб.
4. Спрос на товары А и В меняется соответственно по закону

S_a=100+3t

S_b=2e^t ,

где t – время в месяцах.

Определить, в какой момент S_b станет больше, чем S_a.

Указание: следует найти t такое, чтобы разность S_b - S_a оказалась равной 0.

5. 
   При расчете отпускной цены подакцизного товара поступают следующим образом:
   

1. 
   вначале учитывают норму рентабельности
   

с₁ = S * (100 + r),

где S – себестоимость (руб.)

r – норма рентабельности (в %)

2. 
   находят отпускную цену по формуле:
   

,

где  – акцизная ставка (в %)

Пользуясь электронными таблицами Excel, составить расчет с по данным S, r ,  .

1) Найти с при S = 6000, r = 20%,  = 20%.

2. 
   определить с помощью инструмента Подбор параметра, какой должна быть себестоимостьS, если с=8000(при тех же rи ).
   

6. Валовой доход предприятия в 2004 году составил 100000 $ . В предыдущие 5 лет (начиная с 1999 г.) он изменялся следующими темпами: +10%, +20%, +15%, -30%, +20% .

Определить годовой доход предприятия в 1999 г.
7. Банк ежемесячно начисляет проценты по формуле простых процентов:

---

,

где S – текущий вклад;

P – начальный вклад;

c – простая ставка;

t – время.

Определить время, через которое вклад возрастет в 2 раза.
8. Банк ежемесячно начисляет проценты по формуле простых процентов:

,

где S – текущий вклад;

P – начальный вклад;

c – простая ставка;

t– время.

Определить, каким должна быть исходная сумма, чтобы через 6 месяцев общая сумма вклада оказалась равной 2000 руб.
9. Наследство в 15 млрд. долларов, оставшееся после смерти миллиардера NN, необходимо на основании завещания поделить между наследниками, начиная с родственников первого уровня и заканчивая пятым уровнем родства, соблюдая следующие условия:

– доли родственников одинакового уровня равны;

– доли родственников первого, второго, третьего, четвертого и пятого уровня выраженные в долларах, находятся по отношению друг к другу в следующей пропорции:

x⁵: x⁴: x³: x²: x;

где x – некоторое положительное число, отличное от 1.

Всего оказалось 3 родственника первого уровня, 8 родственников второго уровня, 20 родственников третьего уровня, 75 родственников четвертого уровня и 226 родственников пятого уровня.

Определить, как следует распределить наследство.
10. Цена товара снижалась дважды: вначале на 30%, а затем еще на 10 %, после чего стала равной 120 р. Найти первоначальную цену.
11. Турист побывал в четырех странах. При этом он:

– во Франции он истратил денег в 2 раза больше, чем в Германии;

– в Дании в 3 три раза меньше, чем во Франции;

– в Испании в 1.5 раза больше, чем в Дании.

Определить сколько денег он истратил в каждой стране, если его общие расходы составили 5000$.
12. Банк ежемесячно начисляет проценты по формуле сложных процентов:

,

где S – текущий вклад;

P – начальный вклад;

c – сложная ставка;

t – время.

Определить, через сколько месяцев сумма вклада увеличится в 1.5 раза

13. 
    Один банк начисляет проценты по вкладам по сложным процентам, а второй – по простым (см. задания 2, 7). При заданных значениях ставок определить через сколько месяцев стоимость вклада по сложным процентам превзойдет стоимость вклада по простым процентам.
    

---

13. 
    Начальная цена некоторого товара была равна 100 руб. После двукратного подорожания на одно и то же количество процентов его цена стала равна 144 руб. Найти величину однократной наценки.
    

2.2. Решение систем линейных уравнений
2.2.1. Общие сведения

В некоторых прикладных задачах возникает необходимость в решении систем линейных уравнений. Пусть дана система, состоящая из n линейных уравнений с n неизвестными:

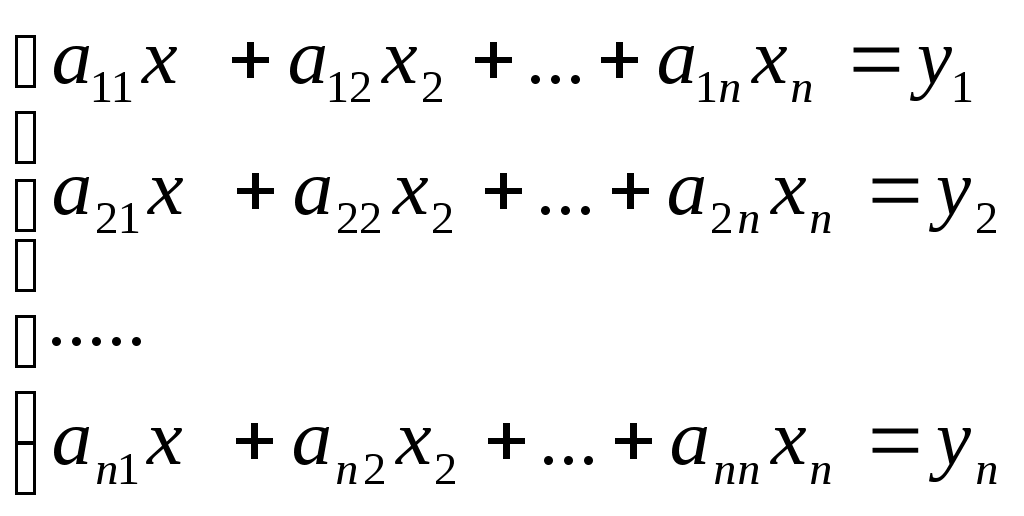(2.2)

В матричном виде система (2.1) имеет вид:
, (2.3)

где А – матрица коэффициентов системы;

X– вектор–столбец неизвестных;

Y – вектор–столбец свободных членов.

Из курса линейной алгебры известно, что если главный определитель системы (2.2) отличен от нуля, то эта система имеет единственное решение. При этом существует матрица А^–1 (обратная к матрице А)и решение системы(2.2) можно найти по формуле:

X =A^–1Y, (2.3)
В MS Excel для решения систем линейных уравнений удобнее всего воспользоваться встроенными матричными функциями МОБР и МУМНОЖ . Первая из них позволяет находить обратную матрицу, а вторая – перемножать две матрицы.
2.2.2. Реализация расчетов в Excel

Пусть дана следующая система уравнений:
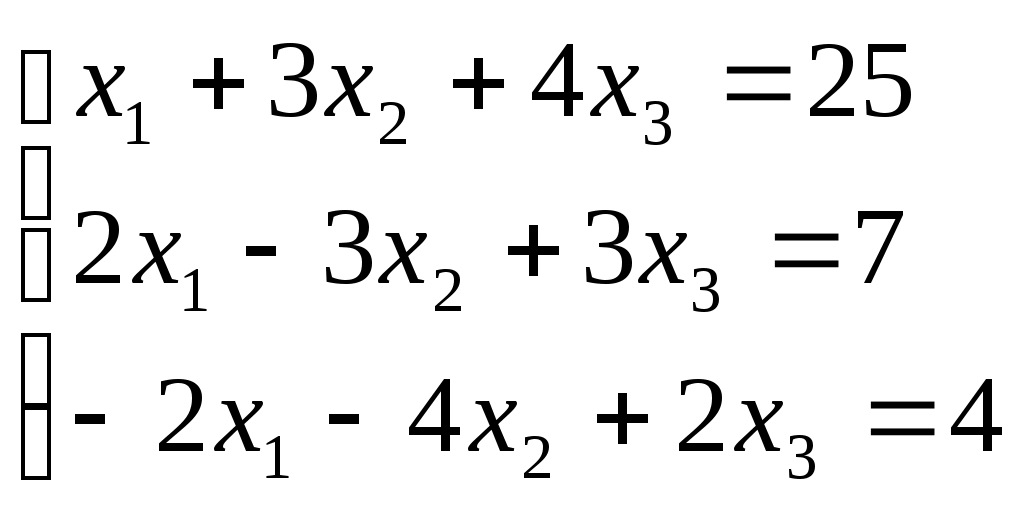(2.4)

В матричном виде уравнение (2.4) выглядит следующим образом:
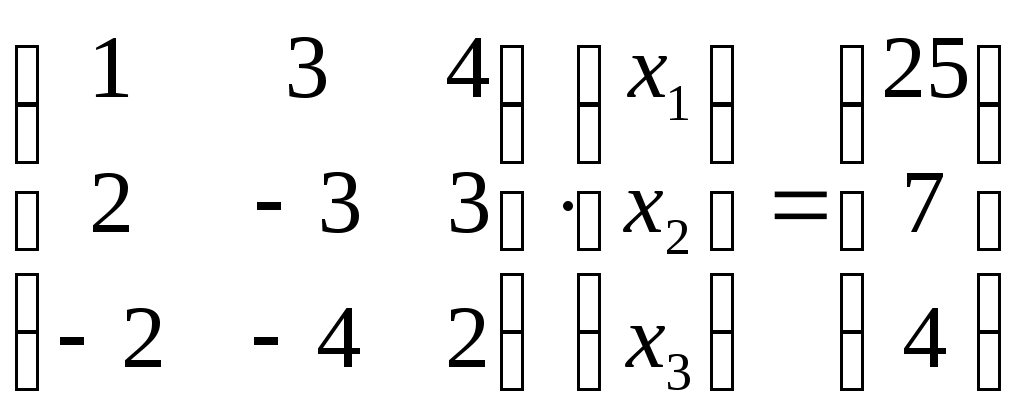(2.4а)

Процесс решения уравнения (2.4) или (2.4а) состоит в последовательном вычислении компонентов уравнения (2.3).

1) В ячейках D5:F7 разместим матрицу коэффициентов;

2) В ячейках H5:H7 разместим вектор–столбец Y;

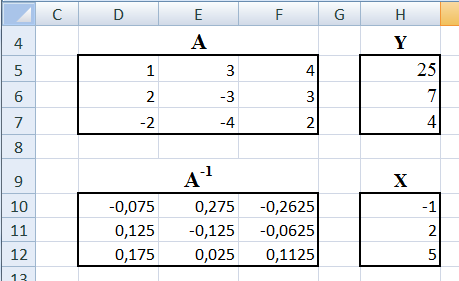
3) Найдем обратную матрицу A^-1.

Для этого:

– курсор устанавливаем ячейку D10;

– вызываем функцию МОБР;

– в качестве аргумента указываем диапазон D5:F7;

---