Файл: Контрольная работа по теме Базы данных в Excel 72 IV. Макросы в ms excel 78 Макросы для автоматизации работ 78.doc

6.2.2. Пример.

В банке был размещен вклад в размере 100 тыс. руб. сроком на 5 лет под 10% годовых. Начисление процентов производится в конце каждого месяца. Найти конечную величину вклада.

Для решения задачи используется функция БС(будущая стоимость), которая имеет следующий формат:

БС(ставка, кпер, плт, пс, тип).
Пусть исходные данные размещены следующим образом:

	A	B	C	D
1
2		Начальный вклад	-100000
3		Время	5
4		Периодичность	12
5		Ставка	10,00%
6		Конечный вклад	164 530,89р.
7

Тогда для решения задачи в ячейку С6 вводится формула:

=БС(C5/C4;C3*C4;0;C2)

Используя функции БС, КПЕР, ПС, СТАВКА, ПЛТ решить следующие задачи.

6.2.3. Варианты заданий

1. Ссуда в размере 1 млн. руб. выдана 20 января 2010 года до 5 октября 2012 года включительно под 18% годовых. Какую сумму должен заплатить должник в конце срока?

2. Выдан кредит в сумме 1 млн. долл. с 15.01.2003 по 15.03.2005 под 120% годовых. Рассчитать сумму погасительного платежа.

3. Ссуда в 20 000 долл. дана на полтора года под ставку 28% годовых с ежеквартальным начислением. Определить сумму конечного платежа.

---

4. Банк принимает вклад на срок 3 месяца с объявленной годовой ставкой 100% или на 6 месяцев под 110%.Как выгоднее вкладывать деньги на полгода: дважды на три месяца или один раз на 6 месяцев?

5. Рассчитать будущее значение вклада 1000 долл.через 1,2,3,4,5 лет при годовых процентных ставках 10%,20%,...,50%. Дополнительные поступления и выплаты отсутствуют.

6. Сумма 2000 размещена под 9% годовых на 3 года. Проценты начисляются раз в квартал. Какая сумма будет на счете?

7. Какова сумма долга через 26 месяцев, если его первоначальная величина 500 000 долл., проценты сложные, ставка — 20% годовых, начисление поквартальное?

8. На счет в банке вносится сумма 10000 долл.в течение 10 лет равными долями в конце каждого года. Годовая ставка 4%. Какая сумма будет на счете через 10 лет?

9. Рассматриваются две схемы вложения денег на 3 года: в начале каждого года под 24% годовых или в конце каждого года под 36%. Ежегодно вносится по 4000. Какая схема выгоднее?

10. На счет была положена некоторая сумма, которая при ставке 21% с начислением процентов два раза в год через два года стала равной 3000000$ Найти исходную сумму, положенную на счет.

11. Рассматриваются два варианта покупки недвижимости: заплатить сразу 70 000 руб. или платить ежемесячно по 800 руб. в течение 12 лет при ставке 9% годовых. Какой вариант более выгоден?

12. За какой срок в годах сумма, равная 75 000 долл., достигнет 200 000 долл. при начислении процентов по сложной ставке 15 % раз в году и поквартально.

13. Пусть в долг на полтора года дана сумма 2000 долл. с условием возврата 3000 долл. Вычислить годовую процентную ставку.

14. Выдан кредит 200 000 долл. на два с половиной года. Проценты начисляются раз в полгода. Определить величину процентной ставки за период, если известно, что возврат составит 260 000 долл.
6.3. Анализ межотраслевого баланса (модель Леонтьева)

1. 
   Основные понятия
   

Пусть экономическая система состоит из трех отраслей:

– промышленный;

– сельскохозяйственный;

– энергетический.

В каждой отрасли для производства расходуются некоторые ресурсы (сырье, оборудование, рабочая сила и т.д.). Эти ресурсы могут быть произведены как самой отраслью, так и другими отраслями. Другими словами каждая отрасль в системе одновременно является и производителем и потребителем.

Основной целью балансового анализа является определение объемов производства каждой отрасли, необходимых для обеспечения потребностей всей экономической системы.

---

В качестве примера в табл. 6.1 приведены объемы производства и потребления для описанной экономической системы.
Таблица 6.1

	Промышленность	Сельское хозяйство	Энергетика	Общий выпуск
Промышленность	50	40	110	200
Сельское хозяйство	70	30	150	250
Энергетика	80	180	40	300
Общее потребление	200	250	300

Из данных таблицы следует, что:

1) Промышленность для собственных нужд расходует:

– 50 ден. ед. собственного производства;

– 70 ден. ед. продукции сельского хозяйства;

– 80 ден. ед. производства энергетической отрасли.

2) Сельское хозяйство для собственных нужд расходует:

– 40 ден. ед. промышленной продукции;

– 30 ден. ед. собственного производства;

– 180 ден. ед. производства энергетической отрасли.

3) Энергетика для собственных нужд расходует:

– 110 ден. ед. промышленной продукции;

– 150 ден. ед. продукции сельского хозяйства;

– 180 ден. ед. собственного производства.

Здесь все отрасли производящие, и они же потребляют всю производимую продукцию.

Для данных табл. 6.1 имеет место баланс между производством и потреблением. Это обусловлено тем, что сумма структурных элементов по столбцам равна 1. Т.е. приведенный пример соответствует тому случаю, в котором вся производимая продукция самими же отраслями и потребляется.

Эта ситуация соответствует так называемой замкнутой модели межотраслевых связей.

Естественно, что такая, работающая сама на себя экономика, практического значения не имеет. В действительности вся произведенная продукция делится на две части:

– одна часть расходуется на собственные нужды в производящих отраслях;

– вторая часть расходуется в сфере потребления (непроизводящих отраслях).

---

Такая система баланса называется открытой.

Ключевым понятием теории межотраслевого баланса является понятие структурной матрицы.

Значения ее элементов показывают долю производства (собственного и других отраслей), необходимую для поддержания производства в данной отрасли.

Проиллюстрируем ее смысл на числовом примере. В табл. 6.2 для некоторой экономики приведены объемы потребления продукции по отраслям.

Таблица 6.2

	Промышленность	Сельское хозяйство	Энергетика
Промышленность	50	40	110
Сельское хозяйство	70	30	150
Энергетика	80	180	40

А в табл. 6.3 приведен общий объем выпуска по отраслям

Таблица 6.3

	Объем выпуска
Промышленность	220
Сельское хозяйство	260
Энергетика	350

Тогда элементы структурной матрицы рассчитываются следующим образом:

Таблица 6.4

	Промышленность	Сельское хозяйство	Энергетика
Промышленность	50/220=0,223	40/260=0,154	110/350=0,314
Сельское хозяйство	70/220=0,318	30/260=0,115	150/350=0,429
Энергетика	80/220=0,364	180/260=0,692	40/350=0,114
Всего	0,909	0,962	0,857

Из данных табл. 6.4 следует, что для поддержания самой себя экономика расходует примерно 91% собственного промышленного производства, 96,2% собственного сельскохозяйственного производства и 85,7% собственного энергетического производства.

Сама по себе структурная матрица является в каком–то смысле первичной, поскольку значения элементов обусловлены спецификой отраслей. Поэтому ее также называют технологической матрицей.

---

2. 
   Математическая модель межотраслевого баланса
   

При построении математической модели вводятся следующие обозначения:

– объем производства в i–ой производящей отрасли;

– объем продукции, произведенной в i–ой отрасли и потребляемой в отрасли j;

– объем продукции i–ой отрасли, расходуемый на народное потребление;

– объем продукции i–ой отрасли, идущий на производство единицы продукции j–ой отрасли. Как указано выше этот параметр называется структурным или технологическим) коэффициентом.

Уравнение баланса сводится к равенству объема выпуска каждого производящего сектора сумме потребления его продукции всеми производящими отраслями и сектором народного потребления:
(6.3)
или, в более развернутом виде:
. (6.4)
Для реализации расчетов уравнения (6.3)–(6.4) обычно представляют в матричной форме.

При этом приняты следующие обозначения:

X – вектор выпуска продукции;

Y – вектор народного потребления;

А – структурная матрица;

Е – единичная матрица, которая имеет вид:
.
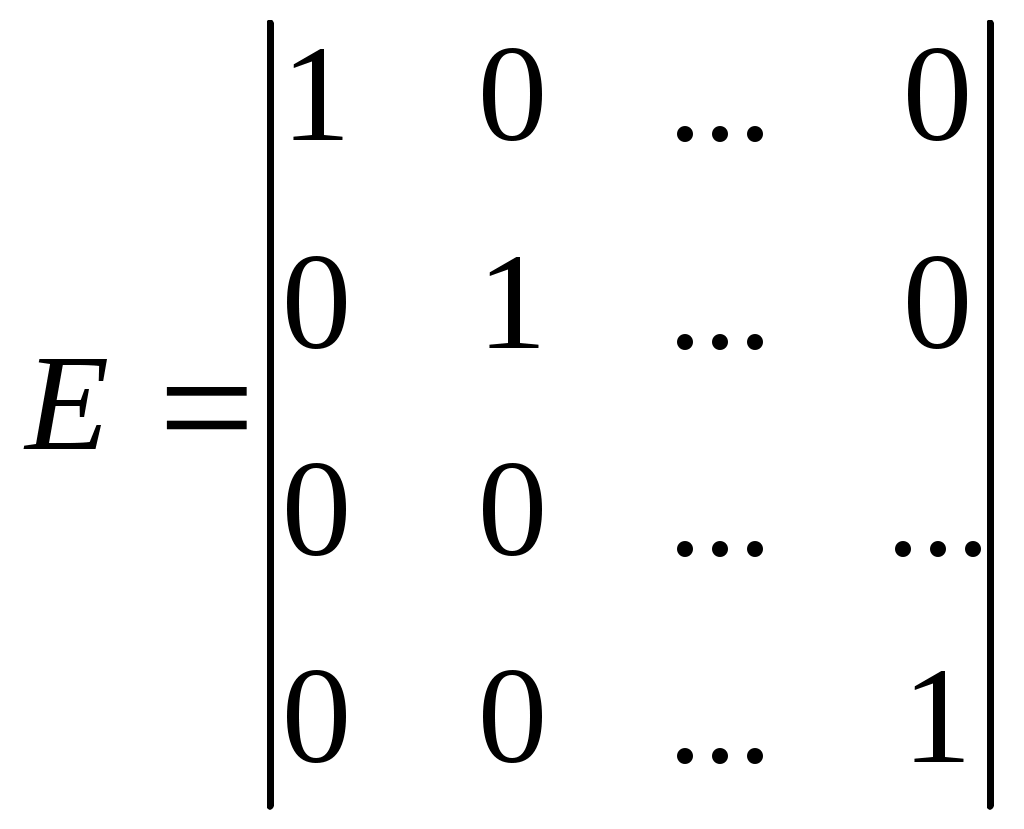Тогда уравнение баланса выражается в виде:
. (6.5)
Уравнение (6.5) является основой для решения многих задач, связанных с анализом и планированием экономики.

Основными такими задачами являются:

– при известной структурной матрице (А) и объемах выпуска (Х) можно определить объемы продукции, идущие на удовлетворение спроса (Y).

– при заданном спросе на продукцию (

---