Файл: Контрольная работа по теме Базы данных в Excel 72 IV. Макросы в ms excel 78 Макросы для автоматизации работ 78.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 788
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Y) определить объемы выпуска (Х).
Первая задача сводится к простому вычислению вектора Y по уравнению (6.5). Решается она путем прямого перемножения матриц (E–A) и X.
Для решения второй задачи используется стандартный метод преобразования матричных уравнений:
– обе части уравнения (6.5) умножаются матрицу, обратную матрице (Е–А):
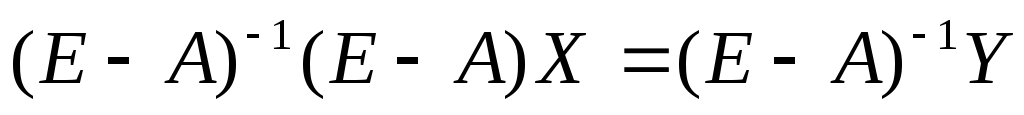 . (6.6)
. (6.6)
Перемножение прямой и обратной матриц дает единичную.
Поэтому уравнение (6.6) приобретает вид:
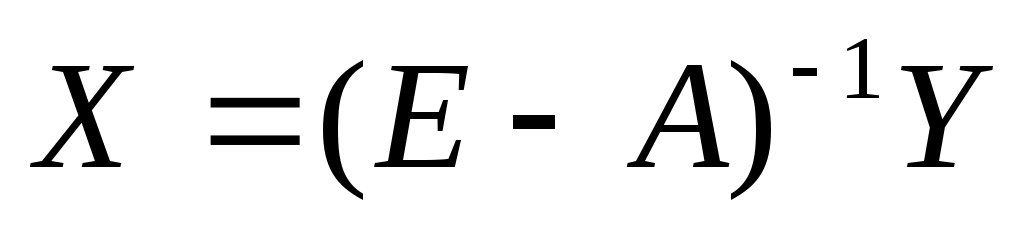 . (6.7)
. (6.7)
Уравнение (6.7) имеет решение только в том случае, если матрица (Е–А) обратима.
Кроме того, исходя из физического смысла, все компоненты вектора Х должны быть больше нуля. Для этого необходимо выполнение условий Хаукинса–Саймона, состоящее в неотрицательности определителей:
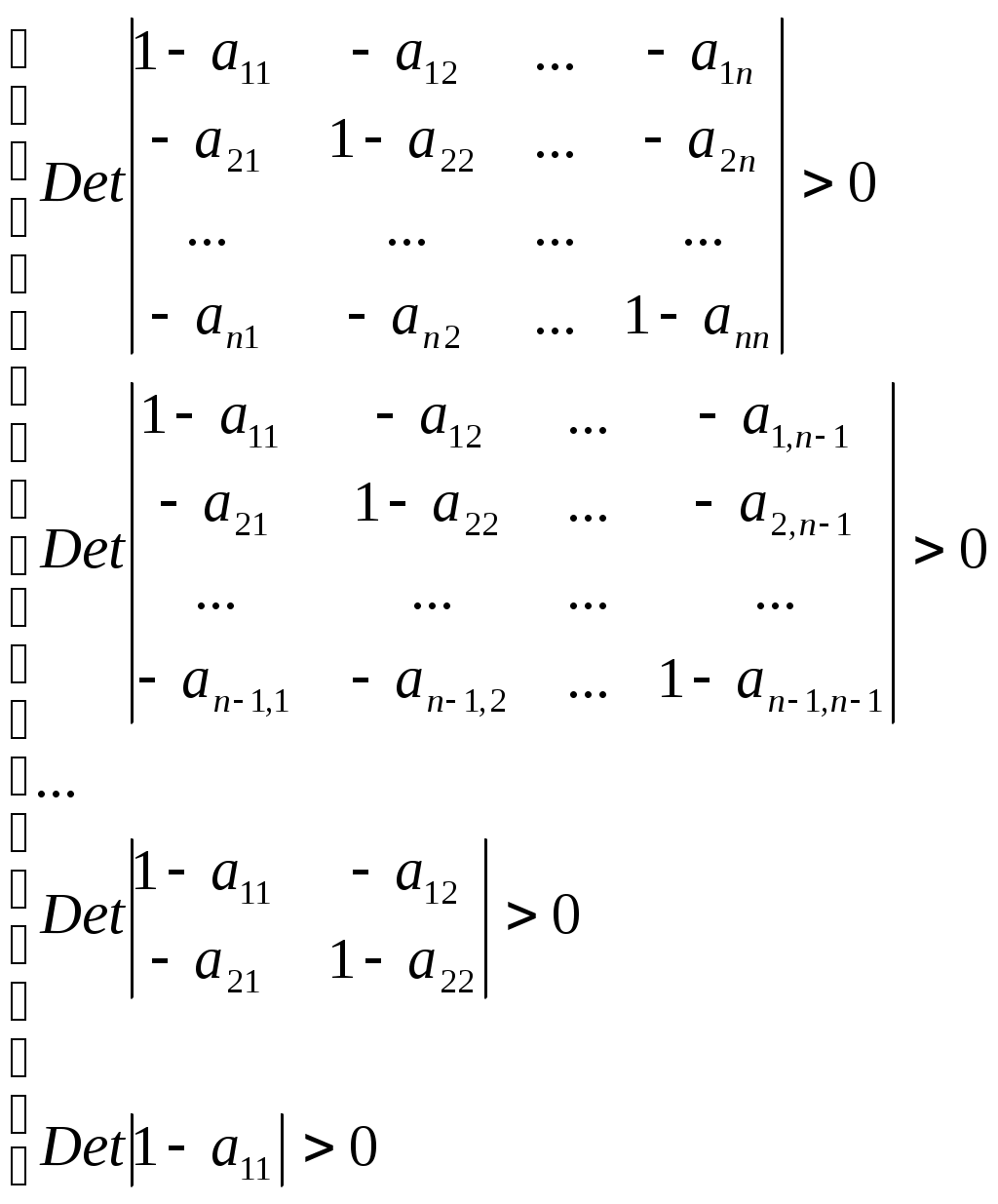 (6.8)
(6.8)
Если все определители системы (6.8) больше нуля, то существующая экономическая система может удовлетворить вектор спроса.
Пример
Пусть экономика характеризуется структурной матрицей, приведенной в табл. 6.5.
Таблица 6.5
Определить объемы производства каждой отрасли, если народное потребление продукции этих отраслей равно:
Для начала решения разместим исходные данные следующим образом:
В соответствии с принятыми в разделе 2 обозначениями присвоим:
– ячейкам C5:E7 имя «А»;
– ячейкам H5:H7 имя «Y»;
– ячейкам C9:E11 имя «E».
В соответствии с уравнением (6.5) поэтапно вычислим необходимые матрицы.
Для вычисления матрицы (Е–А).
1. В C13 вводится формула =E–A.
2. Выделяются ячейки C13:E15.
3.Нажимается клавиша F2 и затем выполняется нажатие Ctrl+Shift+Enter.
4. Ячейкам C13:E15 присваивается имя «ЕА»;
Для вычисления обратной матрицы (E–A)–1
1. В C17 вызывается стандартная функция =МОБР(EА);
2. Выделяются ячейки C17:E19;
3. Нажимается клавиша F2 и выполняется нажатие Ctrl+Shift+Enter;
4. Ячейкам C17:E19 присваивается имя «ЕАобр»;
Для вычисления матрицы X.
1. В C21 вызывается стандартная функция =МУМНОЖ(ЕАобр;Y);
2. Выделяются ячейки C21:С23;
3. Нажимается клавиша F2 и выполняется нажатие Ctrl+Shift+Enter;
В ячейках G13–G15 выполнение условий Хаукинса–Саймона.
1. В ячейку G13 формула =МОПРЕД(C13:E15);
2. В ячейку G14 формула =МОПРЕД(C13:D14);
3. В ячейку G15 формула =МОПРЕД(C13).
Все определители положительны. Поэтому рассматриваемая экономическая система в состоянии удовлетворить заданный спрос.
6.3.4. Варианты заданий
Определить объемы народного потребления продукции и объемы собственного потребления каждой отрасли.
Определить объемы производства каждой отрасли, необходимые для удовлетворения следующих объемов народного потребления:
И даны следующие объемы производства по отраслям:
Определить объемы народного потребления продукции и объемы собственного потребления каждой отрасли.
Первая задача сводится к простому вычислению вектора Y по уравнению (6.5). Решается она путем прямого перемножения матриц (E–A) и X.
Для решения второй задачи используется стандартный метод преобразования матричных уравнений:
– обе части уравнения (6.5) умножаются матрицу, обратную матрице (Е–А):
Перемножение прямой и обратной матриц дает единичную.
Поэтому уравнение (6.6) приобретает вид:
Уравнение (6.7) имеет решение только в том случае, если матрица (Е–А) обратима.
Кроме того, исходя из физического смысла, все компоненты вектора Х должны быть больше нуля. Для этого необходимо выполнение условий Хаукинса–Саймона, состоящее в неотрицательности определителей:
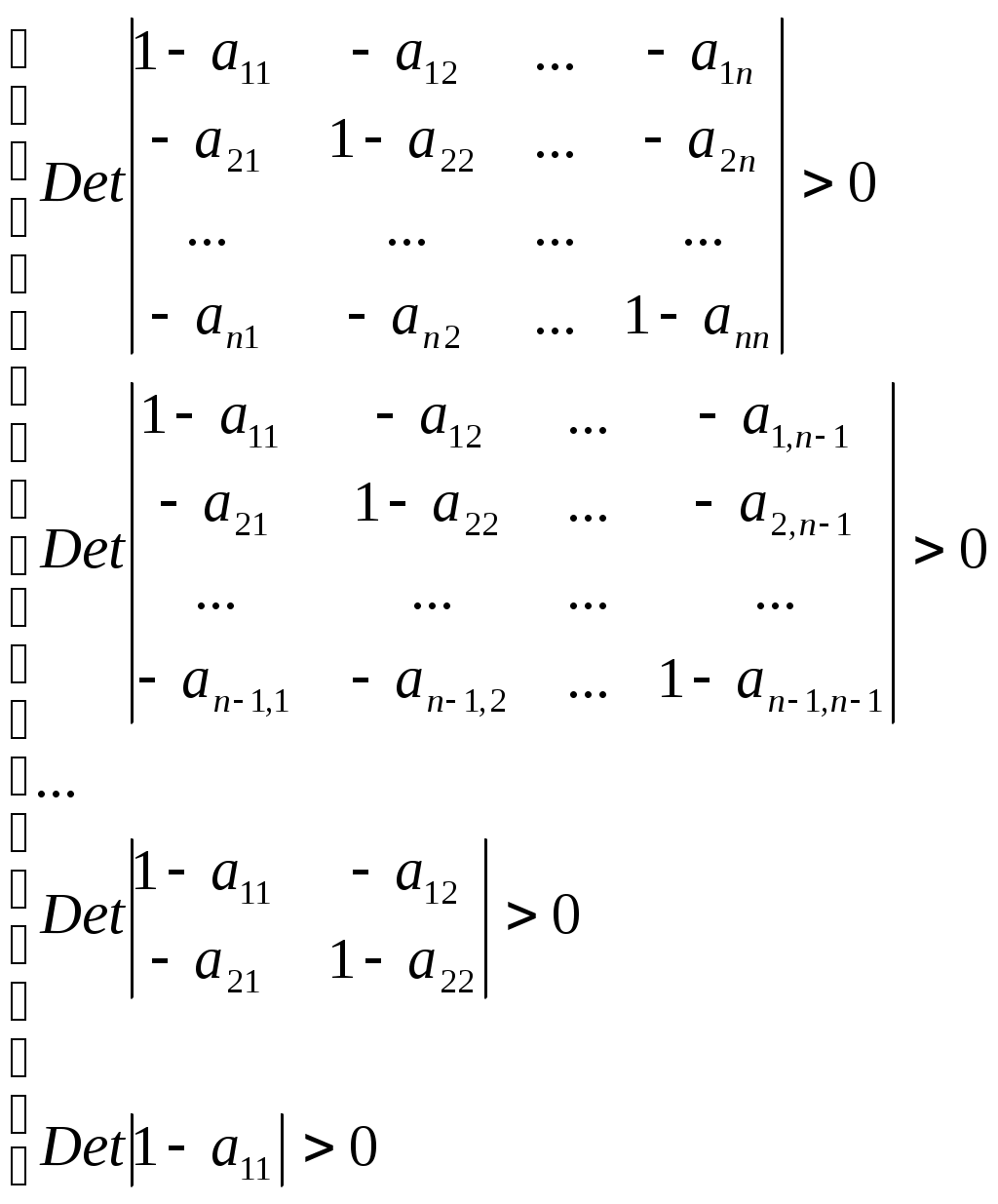 (6.8)
(6.8)Если все определители системы (6.8) больше нуля, то существующая экономическая система может удовлетворить вектор спроса.
- 1 ... 15 16 17 18 19 20 21 22 ... 45
Пример
Пусть экономика характеризуется структурной матрицей, приведенной в табл. 6.5.
Таблица 6.5
| | Промышленность | Сельское хозяйство | Энергетика |
| Промышленность | 0,12 | 0,34 | 0,44 |
| Сельское хозяйство | 0,22 | 0,11 | 0,11 |
| Энергетика | 0,33 | 0,11 | 0,22 |
Определить объемы производства каждой отрасли, если народное потребление продукции этих отраслей равно:
-
промышленная продукция 30 ден. ед.; -
сельскохозяйственное производство 50 ден. ед.; -
энергетика 20 ден. ед.
Для начала решения разместим исходные данные следующим образом:
| | B | C | D | E | F | G | H |
| 3 | | | | | | | |
| 4 | | Промышленность | Сельское хозяйство | Энергетика | | | Потребление |
| 5 | | 0,12 | 0,34 | 0,44 | | | 30 |
| 6 | A= | 0,22 | 0,11 | 0,11 | | Y= | 50 |
| 7 | | 0,33 | 0,11 | 0,22 | | | 20 |
| 8 | | | | | | | |
| 9 | | 1 | 0 | 0 | | | |
| 10 | E= | 0 | 1 | 0 | | | |
| 11 | | 0 | 0 | 1 | | | |
| 12 | | | | | | | |
| 13 | | | | | | | |
В соответствии с принятыми в разделе 2 обозначениями присвоим:
– ячейкам C5:E7 имя «А»;
– ячейкам H5:H7 имя «Y»;
– ячейкам C9:E11 имя «E».
В соответствии с уравнением (6.5) поэтапно вычислим необходимые матрицы.
-
B
C
D
E
F
G
H
13
0,88
–0,34
–0,44
0,389686
14
(Е–А)=
–0,22
0,89
–0,11
0,7084
15
–0,33
–0,11
0,78
0,88
16
17
1,750384
0,80475
1,100886
18
(E–A)–1=
0,533506
1,38881
0,49681
19
0,815785
0,536329
1,817874
20
21
114,7668
22
X=
95,38192
23
87,64749
24
Для вычисления матрицы (Е–А).
1. В C13 вводится формула =E–A.
2. Выделяются ячейки C13:E15.
3.Нажимается клавиша F2 и затем выполняется нажатие Ctrl+Shift+Enter.
4. Ячейкам C13:E15 присваивается имя «ЕА»;
Для вычисления обратной матрицы (E–A)–1
1. В C17 вызывается стандартная функция =МОБР(EА);
2. Выделяются ячейки C17:E19;
3. Нажимается клавиша F2 и выполняется нажатие Ctrl+Shift+Enter;
4. Ячейкам C17:E19 присваивается имя «ЕАобр»;
Для вычисления матрицы X.
1. В C21 вызывается стандартная функция =МУМНОЖ(ЕАобр;Y);
2. Выделяются ячейки C21:С23;
3. Нажимается клавиша F2 и выполняется нажатие Ctrl+Shift+Enter;
В ячейках G13–G15 выполнение условий Хаукинса–Саймона.
1. В ячейку G13 формула =МОПРЕД(C13:E15);
2. В ячейку G14 формула =МОПРЕД(C13:D14);
3. В ячейку G15 формула =МОПРЕД(C13).
Все определители положительны. Поэтому рассматриваемая экономическая система в состоянии удовлетворить заданный спрос.
6.3.4. Варианты заданий
-
Для экономики со структурной матрицей, приведенной в табл. 6.5, даны следующие объемы производства по отраслям:
| Промышленность | 80 |
| Сельское хозяйство | 40 |
| Энергетика | 120 |
Определить объемы народного потребления продукции и объемы собственного потребления каждой отрасли.
-
Дана экономика со следующими объемами производства и собственного потребления:
| | Потребление | Общий выпуск | ||
| | Промышленность | Сельское хозяйство | Энергетика | |
| Промышленность | 50 | 16 | 120 | 220 |
| Сельское хозяйство | 30 | 10 | 180 | 260 |
| Энергетика | 15 | 14 | 140 | 350 |
Определить объемы производства каждой отрасли, необходимые для удовлетворения следующих объемов народного потребления:
| Промышленность | 60 |
| Сельское хозяйство | 70 |
| Энергетика | 20 |
-
Дана экономика со следующей структурной матрицей:
| | Промышленность | Сельское хозяйство | Энергетика |
| Промышленность | 0,20 | 0,40 | 0,3 |
| Сельское хозяйство | 0,12 | 0,10 | 0,10 |
| Энергетика | 0,40 | 0,15 | 0,20 |
И даны следующие объемы производства по отраслям:
| Промышленность | 80 |
| Сельское хозяйство | 40 |
| Энергетика | 120 |
Определить объемы народного потребления продукции и объемы собственного потребления каждой отрасли.
-
Дана экономика со следующими объемами производства и собственного потребления
| | Потребление | Общий выпуск | ||
| | Промышленность | Сельское хозяйство | Энергетика | |
| Промышленность | 50 | 20 | 80 | 220 |
| Сельское хозяйство | 40 | 20 | 20 | 260 |
| Энергетика | 150 | 25 | 50 | 350 |