Файл: Контрольная работа по теме Базы данных в Excel 72 IV. Макросы в ms excel 78 Макросы для автоматизации работ 78.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 772
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
В нашем примере для f = 16 и
| № | 2 | 3 | 4 |
| Ранги | 3,00 | 3,15 | 3,23 |
5. Получить наименьшие значимые ранги путем умножения выписанных рангов на нормированную ошибку.
В нашем случае:
| № | 2 | 3 | 4 |
| НЗР | 3,876 | 4,070 | 4,173 |
6. Произвести сравнение наблюдаемых разностей между средними с вычисленными НЗР по схеме:
разница между рядом стоящими средними сравнивается с минимальным НЗР (при № = 2);
разница между средними через одно сравнивается с НЗР при № = 3;
разница между средними через два сравнивается с НЗР при № = 4 и т. д.
Если НЗР больше наблюдаемых разностей, то сравниваемые средние отличаются несущественно. Иначе различие между средними признается статистически значимым.
В нашем случае:
-
11,8 – 9,8 = 2 <3,876 -
20,6 – 9,8 = 10,8 > 4,070 -
29,8 – 9,8 = 20 > 4,173 -
20,6 – 11,8 = 8,8 >3,876 -
29,8 – 11,8 = 18 > 4,070 -
29,8 – 20,6 = 9,2 > 3,876
В результате сравнения обнаружено, что первое и второе среднее отличаются несущественно, а разница между остальными средними статистически значима.
Результаты сравнения можно наглядно представить на одномерной шкале.
D B A C
9

,8 11,8 20,6 29,8
Здесь средние, отличающиеся несущественно, имеют одну общую черту.
Таким образом по результатам испытаний защитных красок можно сказать следующее:
краски D и B обладают наилучшими защитными свойствами и примерно одинаковы. Наихудшими защитными свойствами обладает краска C. Краска А является промежуточной по защитным свойствам.
7.2.4. Варианты заданий
Варианты заданий взять из Приложения 2 «Районы и города Чувашии в цифрах».
Во всех заданиях методом дисперсионного анализа выяснить имеется ли различие в средних значениях показателя по уровням изучаемого фактора и дать экономическую интерпретацию полученных результатов.
7.3. Регрессионный анализ
7.3.1.Общие сведения
В тех случаях, когда математическая модель процесса неизвестна, для аппроксимации имеющихся данных используются полиномиальные зависимости вида [3]:
где
y – выходной параметр;
x – фактор;
а – коэффициенты уравнения;
n – степень полинома.
Полином первой степени имеет вид:
второй:
третьей:
и т.д.
Основной задачей регрессионного анализа является получение адекватного описания полученных данных полиномом минимальной степени.
7.3.2. Порядок выполнения работы
1. Взять данные своего варианта из Приложения 4 «Транспорт и связь» или открыть файл Транспорт и связь.doc.
2. Скопировать данные своего варианта в новую рабочую книгу. Пусть это будут следующие данные:
| Y (показатель) | X (время) |
| 1 | 0,1 |
| 5 | 0,4 |
| 10 | 0,7 |
| 11 | 1 |
| 10 | 1,3 |
| 8 | 1,6 |
| 7 | 1,9 |
| 8 | 2,2 |
| 7 | 2,5 |
| 6 | 2,8 |
3. Последовательно рассчитать столбцы значений X2, X3 и X4.
| | A | B | C | D | E |
| 1 | Y | X | X2 | X3 | X4 |
| 2 | 1 | 0,1 | 0,01 | 0,001 | 0,0001 |
| 3 | 5 | 0,4 | 0,16 | 0,064 | 0,0256 |
| 4 | 10 | 0,7 | 0,49 | 0,343 | 0,2401 |
| 5 | 11 | 1 | 1 | 1 | 1 |
| 6 | 10 | 1,3 | 1,69 | 2,197 | 2,8561 |
| 7 | 8 | 1,6 | 2,56 | 4,096 | 6,5536 |
| 8 | 7 | 1,9 | 3,61 | 6,859 | 13,0321 |
| 9 | 8 | 2,2 | 4,84 | 10,648 | 23,4256 |
| 10 | 7 | 2,5 | 6,25 | 15,625 | 39,0625 |
| 11 | 6 | 2,8 | 7,84 | 21,952 | 61,4656 |
4. В строке 13 получить уравнение регрессии первой степени. Для этого в B13 вызывается функция
ЛИНЕЙН и в качестве ее аргументов указывается:
известные значения Y – A2:A11;
известные значения X – B2:B11.
В результате выполнения функции в B13 появится число, соответствующее коэффициенту а1 в уравнении (1). Для того, чтобы увидеть второй коэффициент необходимо выделить ячейки B13:C13, затем нажать F2 и затем выполнить тройное нажатие Ctrl+Shift+Enter.
Для обрабатываемых данных получатся следующие значения:
| | A | B | C |
| 13 | Y1= | 0,707071 | 6,274747 |
5. В строке 14 получить уравнение регрессии второй степени. Для этого в B14 вызывается функция ЛИНЕЙН и в качестве ее аргументов указывается:
известные значения Y – A2:A11;
известные значения X – B2:С11.
В результате выполнения функции в B14 появится число, соответствующее коэффициенту а2 в уравнении (2). Для того, чтобы увидеть остальные коэффициенты необходимо выделить ячейки В14:C14, затем нажать F2 и затем выполнить тройное нажатие Ctrl+Shift+Enter.
Для обрабатываемых данных получатся следующие значения:
| | A | B | C | D |
| 14 | Y2= | -3,28283 | 10,22727 | 1,810101 |
6. Аналогично в строках 15 и 16 получить коэффициенты полиномов 3 и 4-ой степени.
7. Используя полученные уравнения регрессии рассчитать предсказываемые с его помощью значения выходного параметра.
Пример расчета по уравнению первой степени:
В G2 вводится формула =$C$13+$B$13*B2, которая затем копируется на весь столбец G. При этом должны получиться следующие значения:
| | A | B | C | D | E | F | G |
| 1 | Y | X | X2 | X3 | X4 | | Y1 |
| 2 | 1 | 0,1 | 0,01 | 0,001 | 0,0001 | | 6,345455 |
| 3 | 5 | 0,4 | 0,16 | 0,064 | 0,0256 | | 6,557576 |
| 4 | 10 | 0,7 | 0,49 | 0,343 | 0,2401 | | 6,769697 |
| 5 | 11 | 1 | 1 | 1 | 1 | | 6,981818 |
| 6 | 10 | 1,3 | 1,69 | 2,197 | 2,8561 | | 7,193939 |
| 7 | 8 | 1,6 | 2,56 | 4,096 | 6,5536 | | 7,406061 |
| 8 | 7 | 1,9 | 3,61 | 6,859 | 13,0321 | | 7,618182 |
| 9 | 8 | 2,2 | 4,84 | 10,648 | 23,4256 | | 7,830303 |
| 10 | 7 | 2,5 | 6,25 | 15,625 | 39,0625 | | 8,042424 |
| 11 | 6 | 2,8 | 7,84 | 21,952 | 61,4656 | | 8,254545 |
По данным столбцов А и G построить совместный график, общий вид которого показан на рисунке. При этом «экспериментальные» данные (столбец А) представлены точками, а рассчитанные – сплошной линией (рис. 7.1).
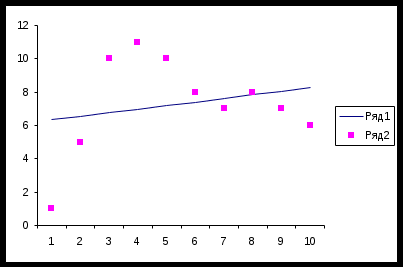
Рис. 7.1. Результат аппроксимации реальных данных линейной зависимостью
И без статистической проверки очевидно, что соответствие между экспериментальными и расчетными данными отсутствует.
В столбцах I, J, K произвести аналогичные расчеты и построения диаграмм для полиномов второй, третьей и четвертой степени. При этом при расчетах уравнения третьей степени в качестве параметра известные значения X указать – B2:D11, а уравнения четвертой степени – B2:E11.
7.3.3. Выбор оптимального уравнения регрессии
По мере увеличения степени полинома наблюдается все более лучшее соответствие между экспериментальными и расчетными данными.
Отметим, что при наличии N измерений максимально возможная степень полинома равна N-1. При использовании полинома максимальной степени будет достигнуто максимальное соответствие между экспериментальными и расчетными данными, т.е. расчетная кривая пройдет по всем экспериментальным точкам.
Однако, интуитивно очевидно, что описывающая кривая не должна быть очень сложной и нет необходимости в идеальном совпадении расчетов с экспериментом. Описание должно быть как можно более простым, а отклонения от него легко объясняется возможными погрешностями в исходных данных.
Поэтому встает вопрос: а на какой степени полинома остановиться?
Для решения этого вопроса предлагается следующая схема вычислений:
-
для каждого уравнения регрессии рассчитывается остаточная сумма квадратов. Для ее расчета используется функция Excel СУММКВРАЗН. Для вышеприведенного примера расчет остаточной суммы квадратов уравнения первой степени производится следующим образом: -
курсор устанавливается в G12, вызывается функция СУММКВРАЗН и в качестве ее аргументов указываются столбцы А и G (A2:A11;G2:G11). -
аналогично в строке 12 столбцов H, I, J производятся расчеты остаточных сумм для полиномов второй, третьей и четвертой степени. -
в F12 отдельно рассчитывается остаточная сумма квадратов для полинома нулевой степени. Для ее расчета в указанную ячейку вводится формула =ДИСПА(A2:A11)*9 (здесь 9 это число измерений минус один); -
дальнейшие расчеты показываются на следующем примере.