Файл: Контрольная работа по теме Базы данных в Excel 72 IV. Макросы в ms excel 78 Макросы для автоматизации работ 78.doc

Пусть для обработки было представлено 10 измерений – N=10.

И пусть в результате расчетов остаточных сумм квадратов для уравнений разных степеней получены следующие результаты:

Степень уравнения	0	1	2	3	4
Остаточная сумма квадратов	10000	4000	155	152	150

Как следует из таблицы, с увеличением степени полинома остаточная суммы квадратов уменьшается, т.е. степень соответствия уравнения описываемым данным увеличивается. В то же время видно, что для больших степеней уменьшение остаточной суммы практически прекращается. Поэтому необходимо объективное правило, согласно которому увеличение степени полинома можно прекратить без ущерба для точности описания данных.
Для решения этого вопроса производятся следующие вычисления.

1. 
   Вычисляются суммы квадратов, приходящиеся на каждую компоненту уравнения. Вычисления производятся по формуле:
   

SS_с = SS_k-1 – SS_k , (7.9)

где

SS_с – остаточная сумма квадратов, для k-ого члена полинома;

SS_k-1 – остаточная сумма квадратов для уравнения (k-1)-ой степени;

SS_с – остаточная сумма квадратов для уравнения k-ой степени.

Для данного примера:

Степень уравнения	0	1	2	3	4
Остаточная сумма квадратов	10000	4000	155	152	150
Сумма квадратов, приходящаяся на компоненту уравнения		6000	3845	3	2

2. 
   Определяются числа степеней свободы для компонент уравнения остаточной суммы квадратов.
   

---

Для каждой компоненты это число равно 1, а для остаточной суммы вычисляется по формуле:

f = N – k – 1, (7.10)

где

N – общее число измерений;

k – количество коэффициентов в уравнении.
Для данного примера:

Степень уравнения	0	1	2	3	4
Число степеней свободы, для компоненты		1	1	1	1
Число степеней свободы на остаточную сумму квадратов (ошибки)		7	6	5	4

3. 
   Определяются величины дисперсий для компоненты и ошибки текущей степени уравнения.
   

Вычисления производятся по формуле:
s² = SS / f. (7.11)

Для данного примера:

Степень уравнения	0	1	2	3	4
Дисперсия для компоненты		6000	3845	3	2
Дисперсия для ошибки		571,42	25,83	30,4	37,5

4. 
   Для каждой компоненты вычисляется критерий Фишера.
   

Вычисления производятся по формуле:
F = s²_k / s²_e , (7.12)

где

s²_k – дисперсия компоненты;

s²_e – дисперсия ошибки.
Для данного примера:

Степень уравнения	0	1	2	3	4
F-отношение		10,5	148,84	0,098	0,0533

5. 
   Для каждой компоненты определяются критические значения критерия Фишера.
   

Эти значения вычисляются с помощью встроенной в Excel функции

---

FРАСПОБР.

Аргументами этой функции являются:

а) уровень значимости.

Если мы хотим сделать свои выводы с надежность 95%, то его значение должно быть равно 0,05.

б) число степеней свободы для числителя.

У нас при вычислении F-отношения в числителе находилась дисперсия компоненты, число степеней свободы которой всегда равно 1.

в) число степеней свободы для знаменателя.

Здесь указывается число степеней свободы для ошибки.
В результате всех вычислений должна получиться следующая сводная таблица.

Степень уравнения	0	1	2	3	4
Остаточная сумма квадратов	10000	4000	155	152	150
Сумма квадратов, приходящаяся на компоненту уравнения		6000	3845	3	2
Число степеней свободы, для компоненты		1	1	1	1
Число степеней свободы для остаточной суммы квадратов		7	6	5	4
Дисперсия для компоненты		6000	3845	3	2
Дисперсия для ошибки		571,42	25,83	30,4	37,5
F-отношение		10,5	148,84	0,098	0,0533
F критическое		5,59	5,98	6,608	7,7086

1   ...   27   28   29   30   31   32   33   34   ...   45

---

Для решения вопроса о статистической значимости компонент уравнения производится сравнение вычисленных значений критерия Фишера с критическими.

Если вычисленное значение больше критического, компонента признается статистически значимой при выбранном уровне надежности. В противном случае компонента признается статистически не значимой.

В данном примере статистически существенными является компоненты первой и второй степени. Компоненты более высоких степеней не существенны. Поэтому для адекватного описания наших данных достаточно использовать уравнение второй степени следующего вида:
. (7.13)
7.3.4. Использование уравнения для прогноза

Пусть нам необходимо найти прогнозируемое значение Y при X=3,1.

Для получения прогнозного значения необходимо подставить нужное значение X в полученное уравнение и вычислить его.

В рассматриваемом случае достаточно скопировать формулу из G16 в G17:

	B	C	D	E	F	G
6		Х (время)	X2	Y (показатель)		Y2
7	1	0,1	0,01	1		2,8
8	2	0,4	0,16	5		5,375758
9	3	0,7	0,49	10		7,360606
10	4	1	1	11		8,754545
11	5	1,3	1,69	10		9,557576
12	6	1,6	2,56	8		9,769697
13	7	1,9	3,61	7		9,390909
14	8	2,2	4,84	8		8,421212
15	9	2,5	6,25	7		6,860606
16	10	2,8	7,84	6		4,709091
17		3,1	9,61			1,966667

---

Таким образом, прогнозируемое значение Y для X=3,1 равно 1,97.

Для оценки точности прогноза сначала рассчитывается стандартное отклонение в точке прогноза:

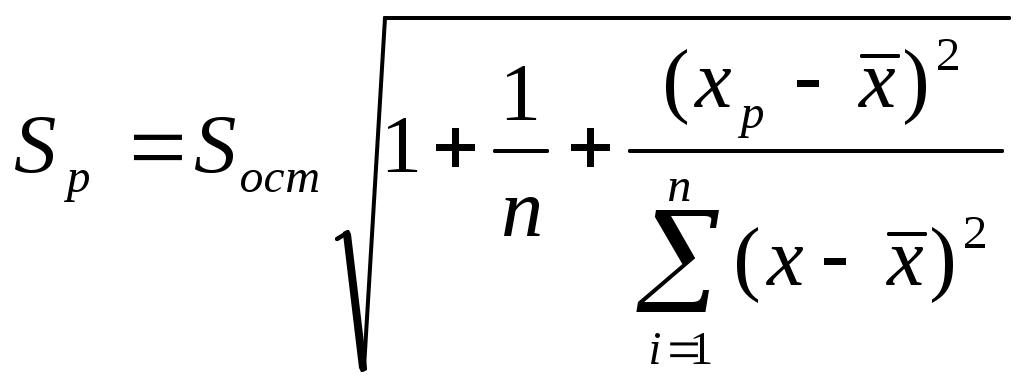, (7.14)

где n – число измерений;

x_p – значение x, для которого осуществляется прогноз;

– среднее значение x, для имеющихся данных;

– стандартное отклонение остаточной суммы квадратов, рассчитываемое по формуле:

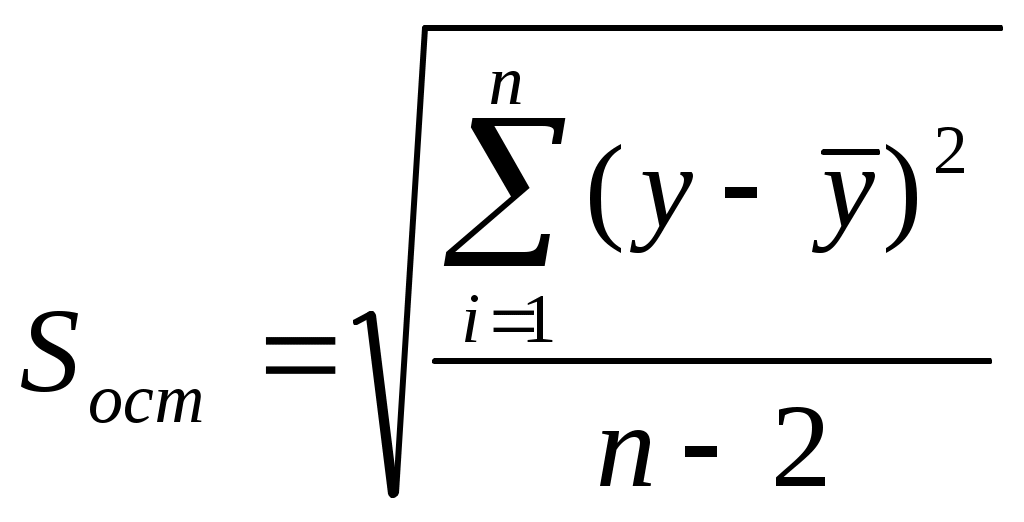. (7.15)
Суммирование в формуле производится по имеющимся значениям y.

Далее рассчитывается доверительный интервал прогноза – dy:

, (7.16)

где t_табл – табличное значение критерия Стьюдента при выбранном уровне значимости и числе степеней свободы, равном n-1.

Результирующий прогноз имеет вид:

. (7.17)
Непосредственно для расчетов:

– в D19 вычислить среднее X

=СРЗНАЧ(C7:C16);

– в D20 вычислить общую дисперсию для Х

=ДИСПА(C7:C16)*9;

– в D21 вычислить общую дисперсию для реальных данных

=ДИСПА(E7:E16)*9;

– в D22 вычислить остаточную дисперсию для уравнения прогноза

=СУММКВРАЗН(E7:E16;G7:G16);

– в D23 вычислить стандартное отклонение для Y

=(D22/8)^(1/2);

– в D24 вычислить точность прогноза

=D23*(1+1/10+(3,1-D19)^2/D20)^(1/2);

– в D25 вычислить критерий Стьюдента

=СТЬЮДРАСПОБР(0,05;9),

где

0,05 – уровень значимости предсказания, что соответствует надежности 1 – 0,05 = 0,95 (95%);

9 – количество реальных данных минус 1.

– в D26 вычислить доверительный интервал
=D25*D24.
В результате должно получиться следующее:

	E	D
19	Среднее X	1,45
20	Дисперсия X	7,425
21	Дисперсия Y	76,1
22	Остаточная дисперсия	26,29697
23	Стандартное отклонение	1,813042
24	Точность прогноза	2,195703
25	Критерий Стьюдента	2,262157
26	Доверительный интервал	4,967025

---