Файл: Контрольная работа по теме Базы данных в Excel 72 IV. Макросы в ms excel 78 Макросы для автоматизации работ 78.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 781
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Пример. Зависимость прибыли (в млн.р.) от количества выпускаемой продукции (тыс. штук) имеет вид:
f(x) = – x2 +12x–10.
Построить график функции f(x) на отрезке [0, 10].
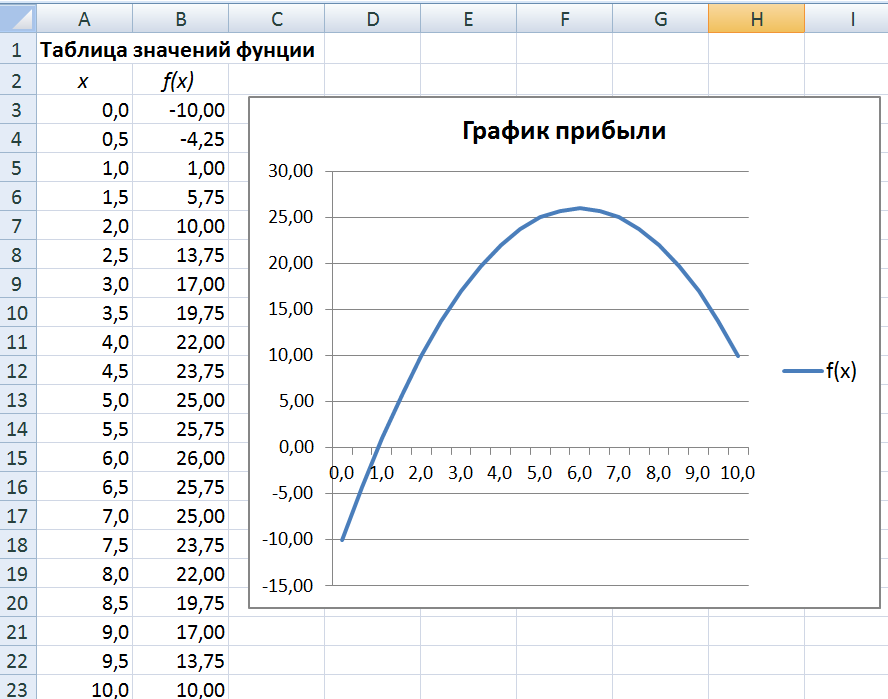
Рис.1.1. График функции одного переменного
Решение.
-
Запишите в столбце A значения аргумента x, для чего, прежде всего, введите в ячейки A3, A4 соответственно значения: 0 и 0,5; после этого выделите диапазон A3:A4 и, ухватившись мышью в правом нижнем углу диапазона за маркер заполнения (рис. 1.2), протяните указатель мыши вниз на нужное количество ячеек.
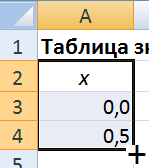
Рис.1.2. Заполнение значений аргумента
-
В ячейку В3 введите формулу:
=-A3*A3+12*A3-10,
которую скопируйте вниз до строки с номером 23.
-
Для построения графика выделите диапазон B2:B23 и с помощью Мастера диаграмм постройте график функции на листе Excel. -
Для того чтобы на оси Ох были представлены значения из диапазона A3:A23, установите указатель мыши на горизонтальной оси, после чего с помощью правой кнопки мыши выберем команду Выбрать данные… и затем с помощью кнопки Изменить укажите диапазон A3:A23 в качестве подписей оси Ох (рис. 1.3).
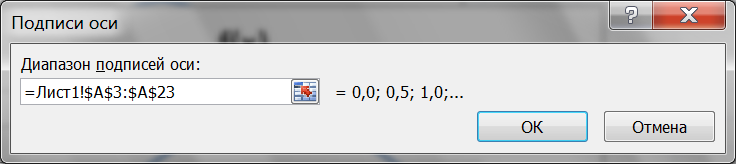
Рис. 1.3. Окно выбора подписи оси Ox.
1.5.3. Варианты заданий
Построить график функции на заданном отрезке:
-
y = x2 – cos x, [-1, 2]; -
y = x – cos x – 2,[1, 3]; -
y =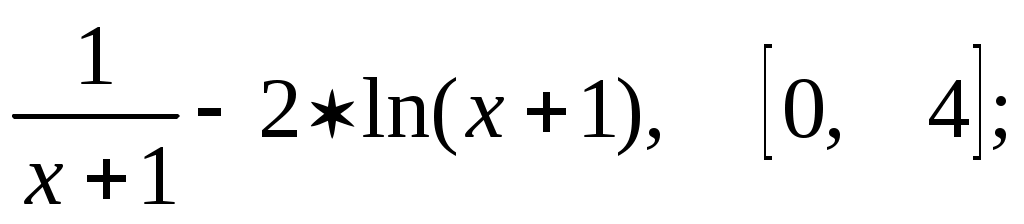
-
y =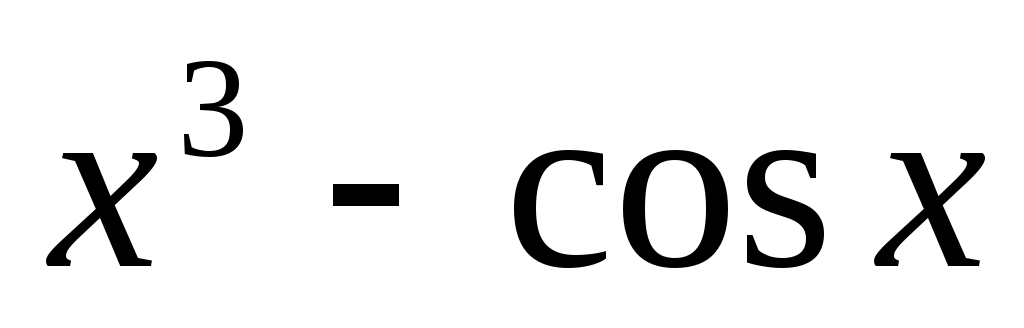 , [-1, 1];
, [-1, 1]; -
y =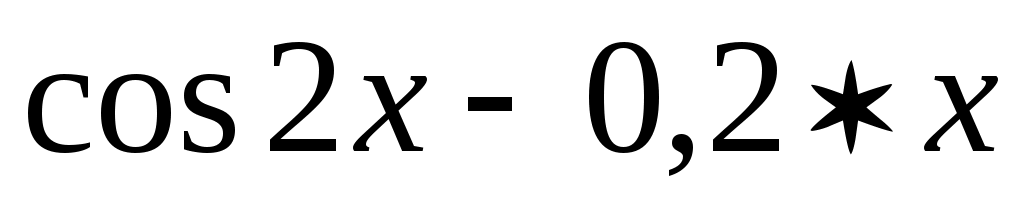 , [ 1, 2];
, [ 1, 2]; -
y =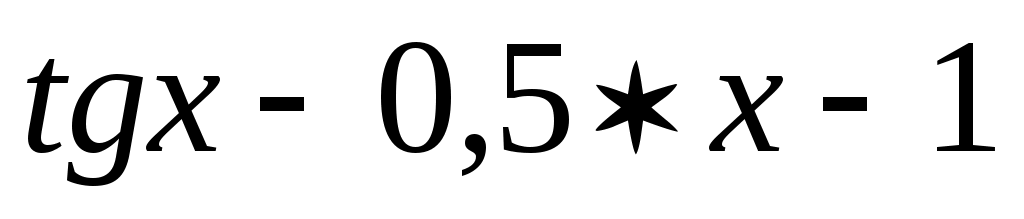 , [-0,5; 0,5];
, [-0,5; 0,5]; -
y =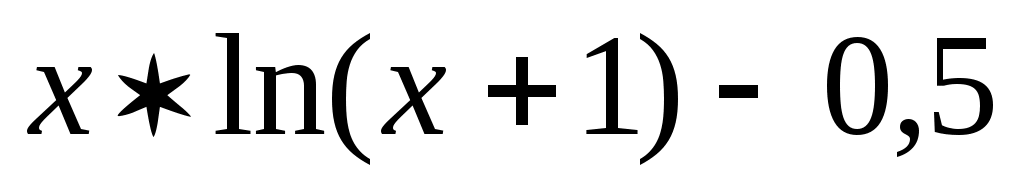 , [1, 5];
, [1, 5]; -
y =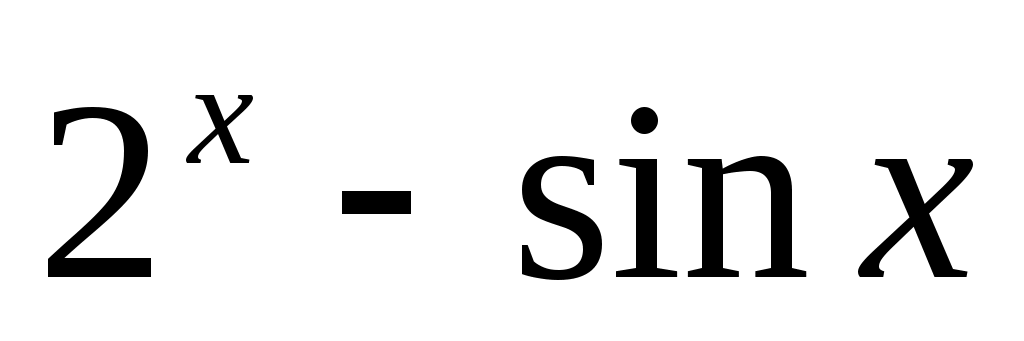 , [-1, 2];
, [-1, 2]; -
y =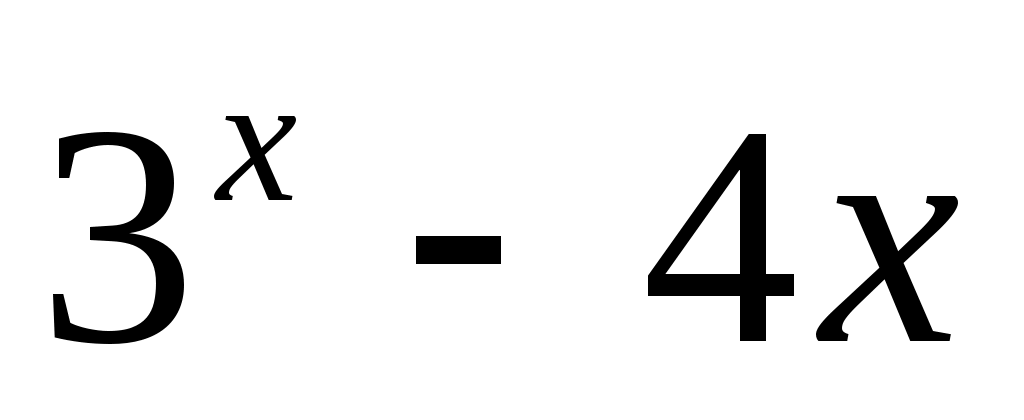 , [0, 2];
, [0, 2]; -
y =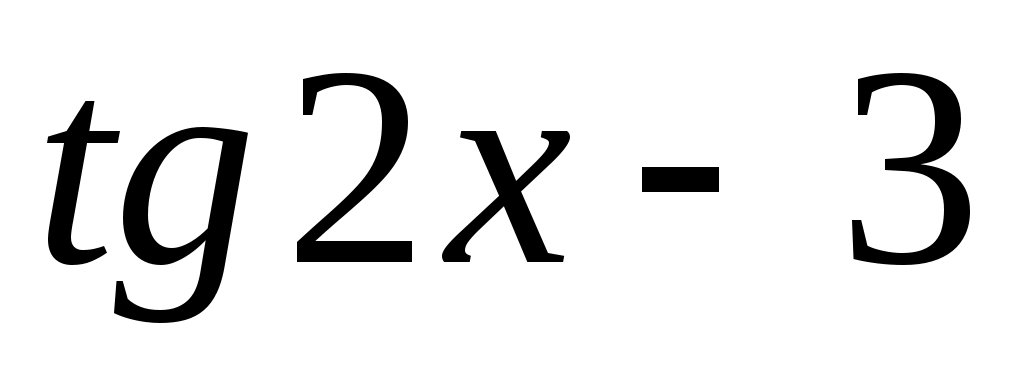 , [-0,5; 0,5];
, [-0,5; 0,5]; -
y =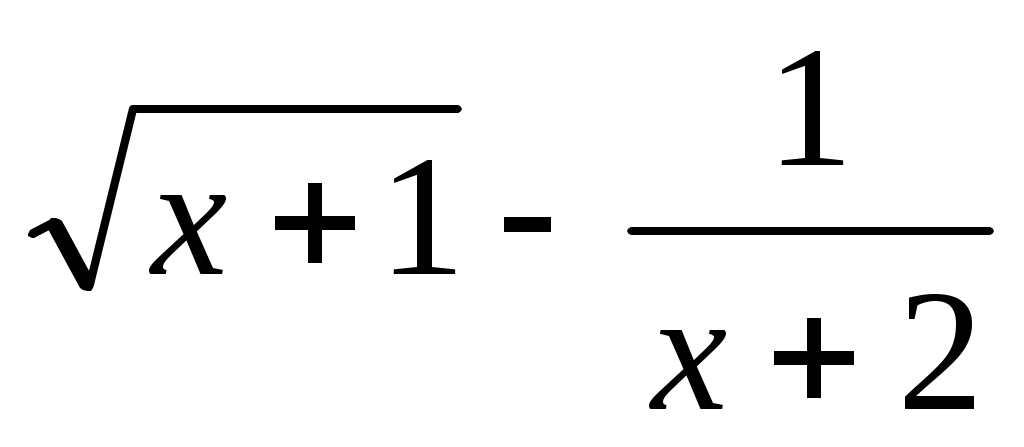 , [1, 5];
, [1, 5]; -
y =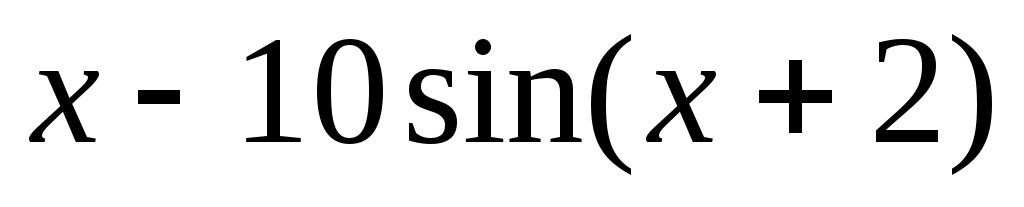 , [-2, 2];
, [-2, 2]; -
y =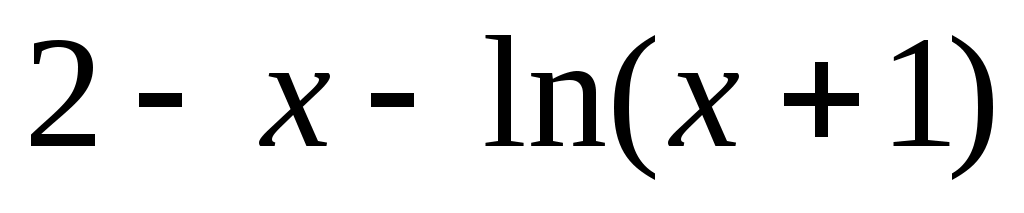 , [0, 5];
, [0, 5]; -
y =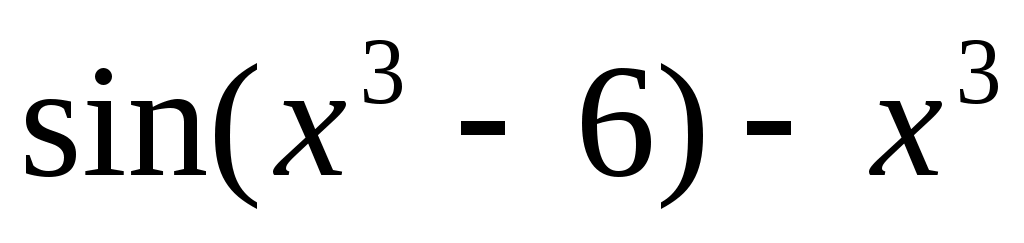 , [-1, 1];
, [-1, 1]; -
y =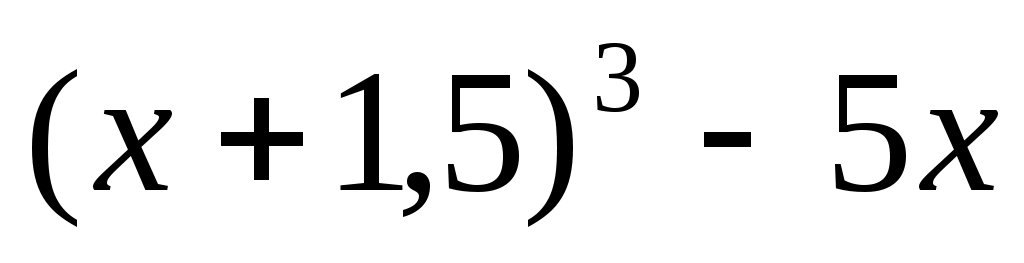 , [-3, 3].
, [-3, 3].
1.6. Собственные функции
1.6.1. Общие сведения
В Excel имеется много встроенных функций. Но если приходится часто вычислять однотипные сложные выражения, то их целесообразно оформить в виде отдельных собственных функций.
Пусть нам необходимо часто вычислять выражение:
Для его вычислении можно создать собственную функцию.
Создание функции состоит из следующих этапов:
1. Командами:
Вид > Панели инструментов > VisualBasic
вызывается редактор Visual Basic.
(В Excel 2010 на ленте надо включить Разработчик (Файл/Параметры/Настройка ленты и в списке Основные вкладки поставить флажок Разработчик и нажать ОК)
2. На появившейся панели выбрать редактор Visual Basic.
3. В редакторе выполнить команды:
Insert > Module и затем
Insert > Procedure
4. Появится окно параметров функции.
Здесь необходимо задать имя функции (Name), например Lenaи переключатель установить в положение Functionи затем Ok
5. Появится заготовка функции вида:
Public Function Lena()
End Function
6. Здесь необходимо:
а) в заголовке - указать имя и тип аргумента, передаваемого функции, а также тип результата, возвращаемый функцией. В данном случае:
Public Function Lena(X As Double) As Double
EndFunction
б) внутри функции - выражение для вычисления. В рассматриваемом примере:
Public Function Lena(X As Double) As Double
Lena = (X ^ 2 + 3 * X + 1) / ( (X – 1) ^ 2 + 5)
End Function
Функция создана.
7. Если сейчас вернуться в Excel, то созданную функцию можно вызвать, используя кнопку «Вставка функций». Если все было сделано правильно, то в категории «Определенные пользователем» должна появиться функция Lena. Работа с ней аналогична имеющимся стандартным функциям.
1.6.2. Общие сведения о Visual Basic for Applications (VBA)
В основе VBA, лежит стандартный Visual Basic, который располагает собственным набором математических операций и встроенных функций. Их список приводится в табл. 1.2, 1.3.
Таблица 1.2
Математические операции
| Операция | Название | Пример | Результат |
| + | Сложение | 3 + 5 | 8 |
| - | Вычитание | 7 - 4 | 3 |
| * | Умножение | 3 * 6 | 18 |
| / | Вещественное деление | 5 / 4 | 1.25 |
| ^ | Возведение в степень | 2 ^ 3 | 8 |
| \ | Целочисленное деление | 7 \ 4 | 1 |
| Mod | Остаток от целочисленного деления | 7 Mod 4 | 3 |
Таблица 1.3
Математические функции
| Название | Обозначение | Запись в Бейсике | Пример | Результат |
| Синус | Sin(x) | Sin(x) | Sin(0) | 0 |
| Косинус | Cos(x) | Cos(x) | Cos(0) | 1 |
| Тангенс | Tg(x) | Tan(x) | Tan(0.785) | 1 |
| Арктангенс | ArcTan(x) | Atn(x) | Atn(1) | 0,785 |
| Натуральный логарифм | Ln(x) | Log(x) | Log(10) | 2,302585 |
| Модуль числа | │x│ | Abs(x) | Abs(-12) | 12 |
| Экспонента | ex | Exp(x) | Exp(1) | 2,718282 |
| Целая часть числа | | Int(x) | Int(99,8) Int(-99,8) Int(-99,2) | 99 -100 -100 |
| Отсечение дробной части числа | | Fix(x) | Fix(99,2) Fix(-99,2) Fix(-99,8) | 99 -99 -99 |
| Корень квадратный | | Sqr(x) | Sqr(9) | 3 |
| Знак числа | | Sgn(x) | Sgn(3) Sgn(0) Sgn(-3) | 1 0 -1 |
Вычисление сложных выражений
Вычисления в сложных выражениях производятся слева направо с учетом приоритета операций.
| Название | Обозначение | Приоритет |
| возведение в степень | ^ | 1 |
| умножение, деление | *, / | 2 |
| сложение, вычитание | +, - | 3 |
Сначала выполняются операции высшего приоритета, затем более низкого. Если приоритет соседних операций одинаков, то сначала выполняется левая. Используя круглые скобки можно изменить порядок вычислений.
Примеры записи математических выражений приведены в табл. 1.4.
Таблица 1.4
| Выражение | Запись в Visual Basic |
| x+3 | X+3 |
| | (X+Y)/4 |
| | X+Y/4 |
| | Log(2*X^2) |
| | Exp(-Abs(X)) |
| | (X+5)^(1/3) |
| | Log(3*X+5)/Log(10) |
| | Sin(X)^2+Cos(X^2) |
| | (Log(Abs(x^(5/3))/Log(7))^2 |
При вычислении сложного выражения удобнее разбить его на ряд простых, вычислить их отдельно и только затем вычислить исходное.
Например
Нам необходимо создать собственную функцию, которая вычисляет выражение:
Выражение очень сложное. В частности, при его наборе очень легко ошибиться в расстановке скобок. Для снижения вероятности ошибок его можно разбить на три части и вычислить отдельно каждую из них. Тогда текст собственной функции будет иметь вид:
FunctionLena(XasDouble) AsDouble
A = 1+ Exp(- X^2) + Sqr(Tan(Abs(X)) – 1 / Tan(1 / X))
B = Log(1 + X^4) / Log(3) – (Sin(X) + Cos(X))^(1 / 5)
C = Atn(X / 2) – 3
Lena = A / B * C
EndFunction
1.6.3. Варианты заданий
Создать собственные функции согласно таблице 1.5.
Номер задания соответствует номеру студента по классному журналу. Проверочные значения позволяют проверить правильность составленных выражений без калькулятора.
Таблица 1.5
| № | F(x) | Проверочные значения | |
| X1 | X2 | ||
| 1 | | 2 | 4 |
| 2 | | 1 | 3 |
| 3 |  | 1 | 3 |
| 4 | | 2 | 5 |
| 5 | | 1 | 4 |
| 6 | | 1 | 5 |
| 7 | | 1 | 4 |
| 8 |  | 1 | 2 |
| 9 |  | 3 | 5 |
| 10 |  | 4 | 6 |
| 11 | | 1 | 3 |
| 12 | | 1 | 5 |
| 13 | | 1 | 5 |
| 14 |  | 2 | 5 |
| 15 | | 1 | 5 |