ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 85
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Вариант | Схема |  |  |  |  |  |  |  |  |  |
| 18 | е | 1,1 | 3 | 5 | 12 | 0,7 | 0,1 | 0,95 | 0,3 | 0,6 |
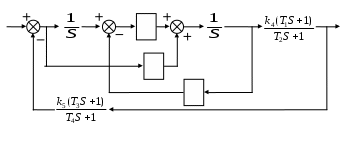
Для структурной схемы САУ, соответствующей выбранному варианту, выполнить следующие действия:
-
Избавиться от всех перекрестных параллельных и обратных связей, привести структурную схему к стандартному виду. Определить передаточную функцию разомкнутой системы, записать ее в стандартной форме. Определить степень астатизма системы. -
Определить амплитудно-фазовую, вещественную и мнимую частотные характеристики разомкнутой системы. -
Построить годограф АФЧХ разомкнутой системы. -
Найти выражения для асимптотической ЛАЧХ и ЛФЧХ разомкнутой системы. -
Построить в масштабе ЛАЧХ и ЛФЧХ разомкнутой системы. -
Определить устойчивость замкнутой САУ с помощью критерия Найквиста и логарифмических частотных характеристик. -
Найти запасы устойчивости системы по фазе и амплитуде. -
Найти передаточную функцию замкнутой системы и проверить выводы пункта 6 с помощью алгебраических критериев Рауса и Гурвица. -
Проверить выводы пункта 6 с помощью частотного критерия Михайлова.
10) Найти коэффициенты С0, С1, С2 ошибок системы.
11) Построить с помощью ЭВМ переходную функцию замкнутой системы и оценить основные показатели качества регулирования (перерегулирование, и время регулирования) в системе.
Расчетная схема имеет вид:
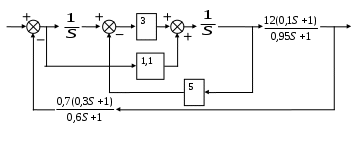
Задание 1. Определить передаточную функцию разомкнутой системы, привести ее к стандартной форме записи.
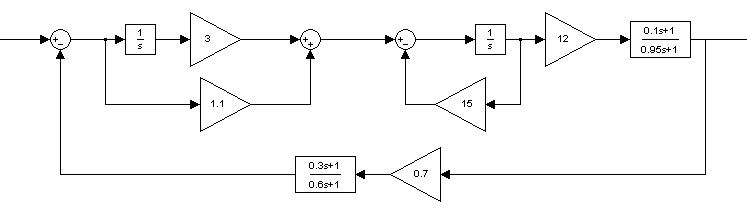
Схема на рисунке состоит из 6 звеньев с передаточными функциями:
; 
; 
; 
; 
;
при этом звенья 1 и 2 параллельны, звено 3 охвачено локальной обратной связью со звеном 4 в цепи ОС. Найдем эквивалентные передаточные функции:
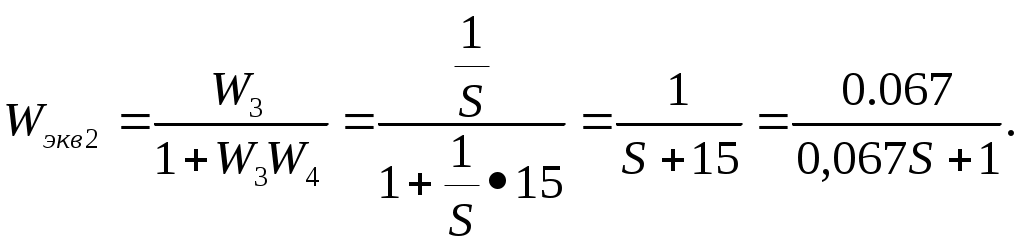
Канонический вид структурной схемы имеет следующий вид:
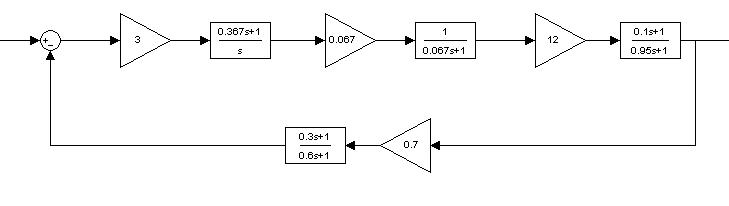
Передаточная функция прямой цепи:
Передаточная функция разомкнутой цепи:
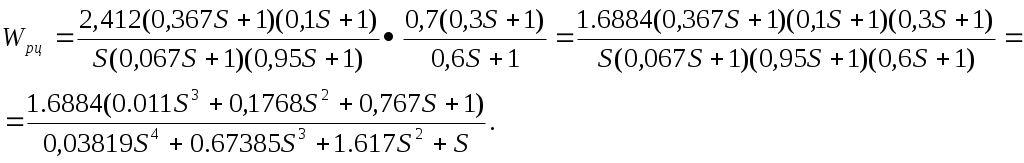
Степень астатизма
Коэффициент передачи К=1,6884. Постоянные времени:
– в числителе, 
– в знаменателе.Задание 2. Частотная передаточная функция системы
:
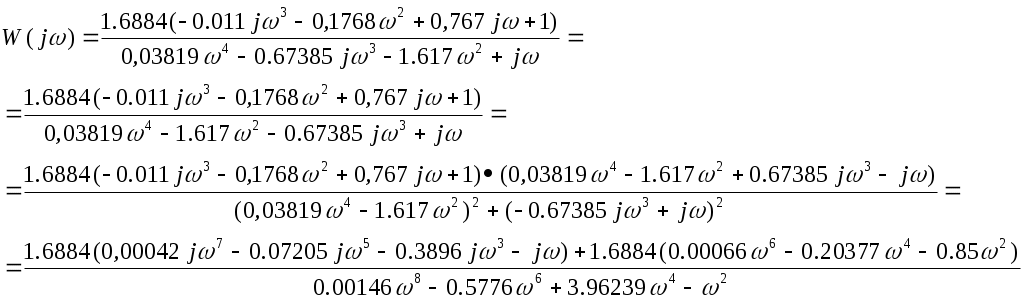
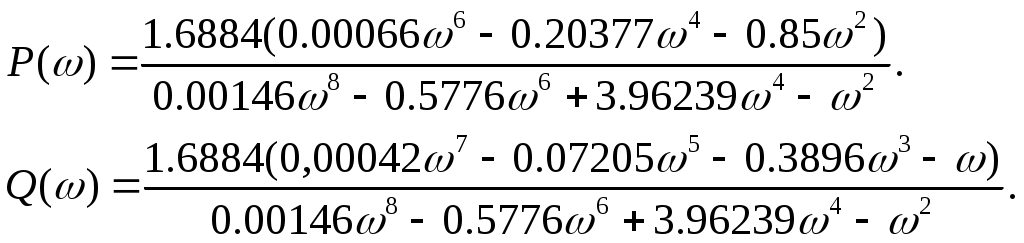
Особые точки АФЧХ приведены в таблице:
 | 0 |  |
 | -1,43 | 0 |
 |  | 0 |
Задание3. Годограф АФЧХ при = 0 начинается в третьем квадранте. К нулю при 0 стремится также из третьего квадранта (рисунок). Пересечений с осями нет.
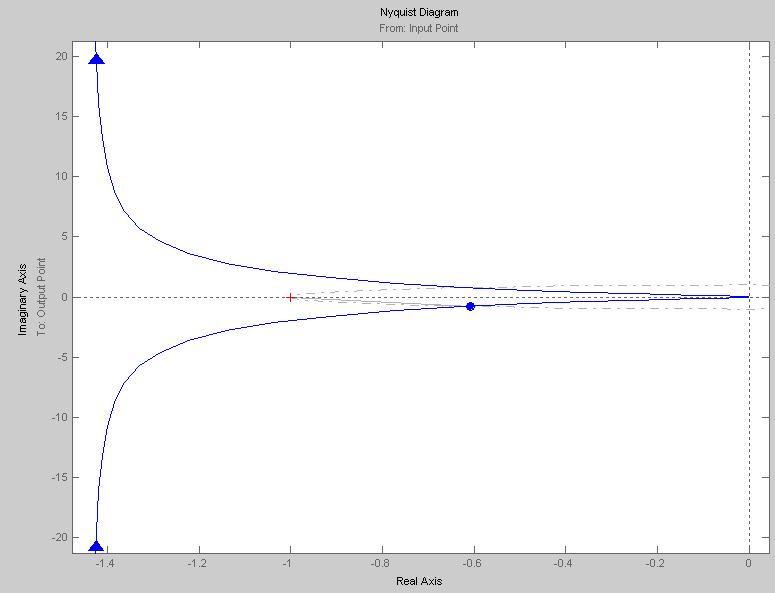
Задание 4. Асимптотическая ЛАХ:
Асимптотическая ЛФХ:
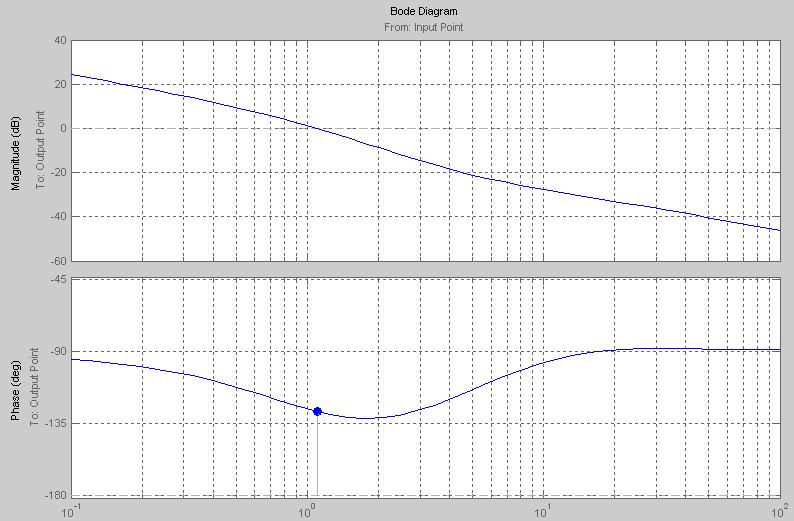
Задание5. Построение в масштабе ЛАХ и ЛФХ системы.
1.Начальный наклон ЛАХ: -20 дБ/дек
2. Значение ЛАХ при = 1 равняется 20lgK, где K – общий коэффициент передачи разомкнутой системы. K = 1,6884, следовательно ЛАХ пересекает ось ординат на уровне 4,55.
3. Строим таблицу значений сопрягающих частот .
T | 0,95 | 0,6 | 0,367 | 0,3 | 0,1 | 0,067 |
| | 1,053 | 1,67 | 2,725 | 3,(3) | 10 | 14,925 |
| Изменение наклона (дБ/дек) | -20 | -20 | +20 | +20 | +20 | -20 |
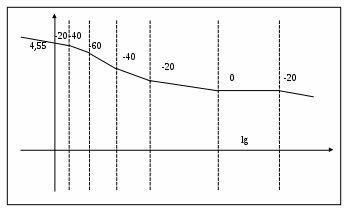
На рисунке изображены в масштабе ЛАХ и ЛФХ системы.
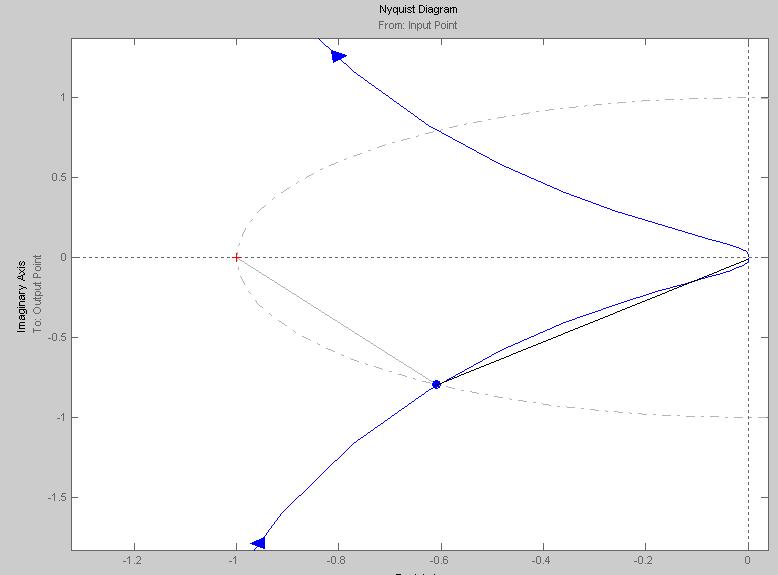
Задание 6.
Для того, чтобы замкнутая система автоматического управления была устойчива необходимо и достаточно, чтобы годограф амплитудно-фазовой характеристики разомкнутой системы, дополненный окружностью бесконечно большого радиуса до положительной действительной полуоси при изменении частоты от 0 до + не охватывал точку с координатами (-1, j0).
Так как в моем случае эта точка не охватывается годографом, то замкнутая система будет устойчива (рисунок задание 3).
Задание 7.
Запас устойчивости по фазе составляет 52,5º. Как видно из рисунка годограф не пересекает отрицательную вещественную полуось, следовательно, запас устойчивости по амплитуде 100%.
Задание8.
Передаточная функция замкнутой системы может быть найдена по следующей формуле:
,где
; 
.Следовательно, передаточная функция замкнутой системы будет равна:
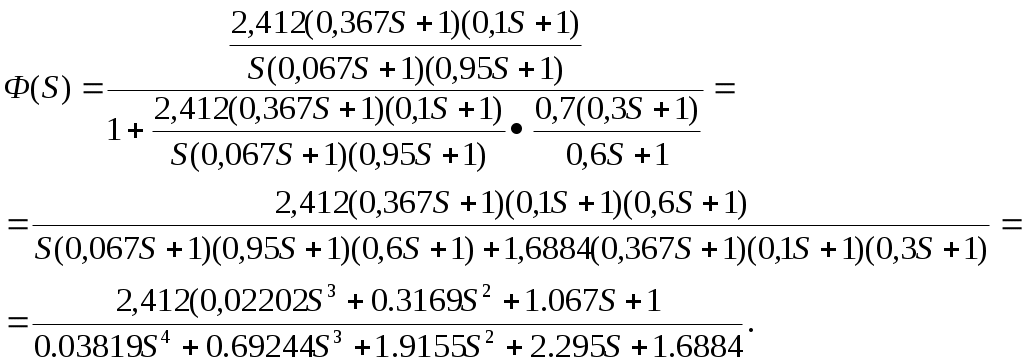
Характеристический полином системы:
Определение устойчивости замкнутой системы методом Рауса. Таблица Рауса имеет следующий вид:
 |  |  | 0 |
 |  | 0 | 0 |
 |  | 0 | 0 |
 | 0 | 0 | 0 |
 | 0 | 0 | 0 |
Где
- четные коэффициенты характеристического полинома,
- нечетные коэффициенты характеристического полинома,
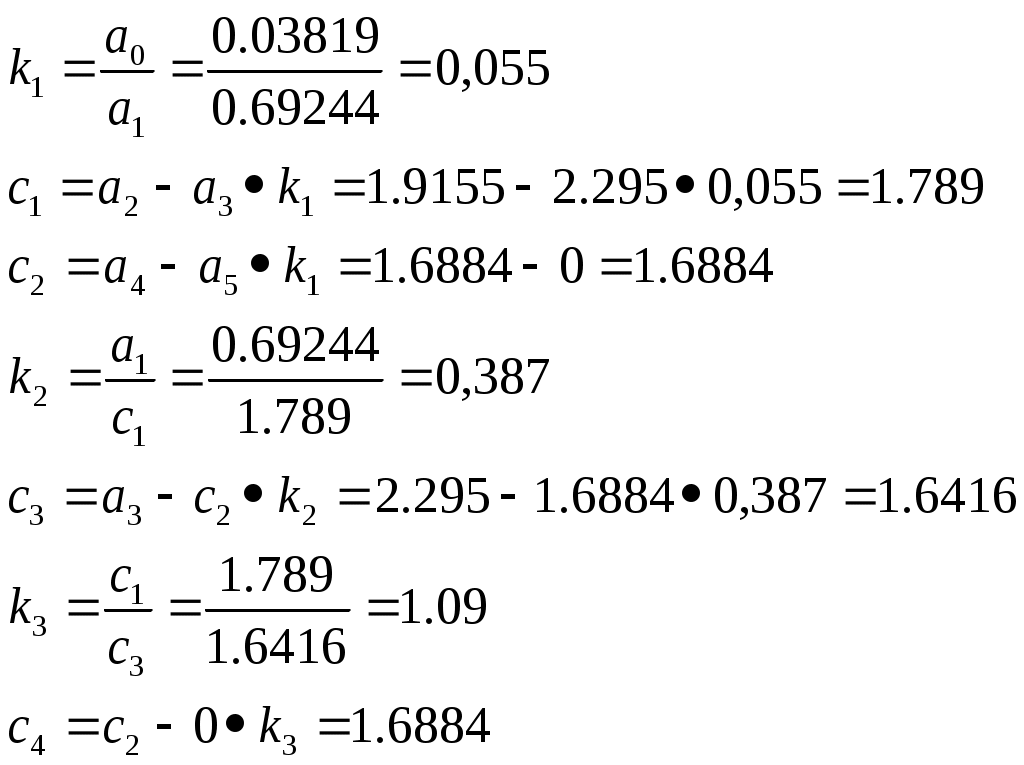
| 0,03819 | 1,9155 | 1,6884 | 0 |
| 0,69244 | 2,295 | 0 | 0 |
| 1,789 | 1,6884 | 0 | 0 |
| 1,6416 | 0 | 0 | 0 |
| 1,6884 | 0 | 0 | 0 |
Все элементы первого столбца имеют один и тот же знак, следовательно характеристический полином замкнутой системы имеет корни только в левой половине комплексной плоскости. Замкнутая САУ устойчива.
Определение устойчивости замкнутой системы методом Гурвица. Строим соответствующие заданной системе определители Гурвица.
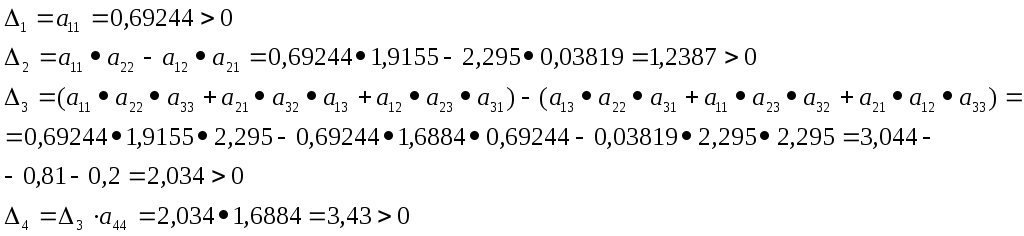Все определители Гурвица положительны, следовательно, характеристический полином замкнутой системы имеет корни только в левой половине комплексной плоскости. Замкнутая САУ устойчива.Задание 9.
Характеристический полином системы:
Вещественная функция Михайлова:
Мнимая функция Михайлова:
Решим уравнения:
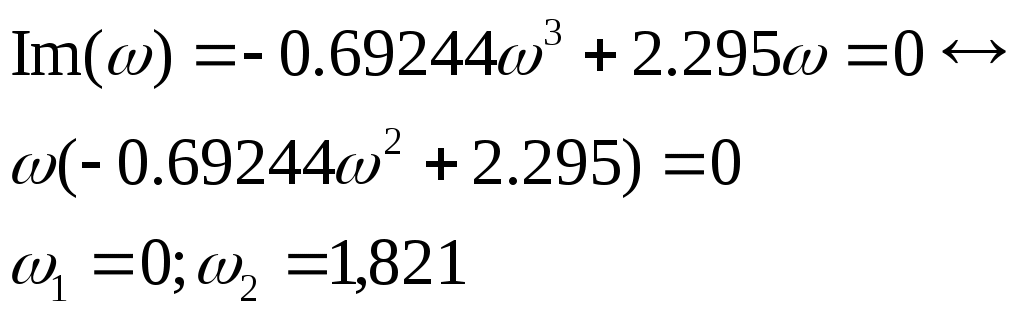
 | 0 | 0,947 | 1,821 | 7,019 |
 | 1,6884 | 0 | -4,244 | 0 |
 | 0 | 1,585 | 0 | -233,338 |