Файл: ИНженеры 1,2Матем.doc

6. Определим уравнения асимптот графика функции. Для определения уравнения асимптоты y=kx+b вос­пользуемся формулами:

Имеем

Чтобы найти искомый предел, дважды применяем правило Лопиталя:

Итак, кривая не имеет асимптот.

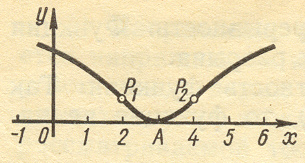
0. Использование производной в задачах прикладного характера.

Задача 1. Найти такой цилиндр, который имел бы наибольший объём при данной полной поверхности S.

Решение: Пусть радиус основания цилиндра равен x, а высота равна y.

Тогда

Следовательно, объём цилиндра выразится так:

Задача сводится к исследованию функции V(x) на максимум при x > 0.

Н

_{и приравняем её к нулю, откуда}

айдём производную

Найдём

П

_{выполняется условие}

_{,то объём имеет,}

ри

_{наибольшее значение причем}

_{т.е осевое сечение цилиндра должно быть квадратом.}

Ответ: Цилиндр с квадратным сечением имеет наибольший объём при данной полной поверхности S.

План действий при решении задач прикладного характера.

1. Обозначить некоторую неизвестную величину прикладной задачи переменной x.

2. Записать ту величину, которая должна быть по условию наименьшей ( наибольшей ) как функцию переменной x.

3. Исследовать полученную функцию на экстремум, используя производные 1-го порядка и второго порядка, найти значение x, соответствующее точке экстремума исследуемой функции.

4. Записать ответ, вернувшись к прикладному значению x.

0. Нахождение наибольшего и наименьшего значения функции на отрезке.

Задача. Найти наибольшее и наименьшее значения функции:

на сегменте -2; 2

Решение: Найдём критические точки и исследуем их на экстремум.

В точке x=0 функция имеет максимум, равный f(0)=3.

В каждой из точек x=-1 и x=1 функция имеет минимум, равный f (-1)=f (1)=2

Найдём значения функции на концах сегмента :

Итак , наибольшее значение равно 11, а наименьшее 2.

Задача . Найти радиус кривизны и координаты центра кривизны кривой в точке А (0; 1).

Решение: Радиус кривизны вычисляется по фор­муле:

Дважды дифференцируя данную функцию, находим

Вычислим значения производных у' и у" в заданной точке А (0; 1), т.е. при x = 0; имеем y¢(0) = 2; y¢¢ (0) = - 4.

Тогда радиус кривизны:

Для нахождения координат центра кривизны С(x_с; y_с] воспользуемся формулами:

Подставив в эти формулы координаты точки А и найден­ные значения производных, получим:

Итак, точка С (5/2; -1/4) — центр кривизны.

Кривая , точка А (0; 1), центр кривизны С (5/2; -1/4) и радиус кривизны R»2,8 .

Задача. Найти радиус кривизны кривой r = a sin3 j (трех лепестковая роза) в точке A (p/6; а).

Решение. Если кривая задана в полярной системе координат уравнением r=f (j), то ра­диус кривизны вычисляется по фор­муле:

Дважды дифференцируя данную функ­цию r= a sin 3j , найдем

---

Вычислим значения производных r¢ и r¢¢ в точке A (p/6;a), т.е при j=p/6 и r =a.

Имеем: r¢ (p/6)=0 и r¢¢ (p/6)=-9a. Подставив в формулу r =a, r¢=0 и r¢¢=9a, получим

Вопросы для самопроверки.

1. Сформулируйте признаки возрастания (убывания) функции. Приведите примеры.

2. Дайте определение экстремума функции.

3. Как найти максимум, минимум функции (два правила)?

4. Приведите пример, когда обращение производной в нуль не является достаточным условием экстремума функции.

5. Как найти интервалы выпуклости (вогнутости) функции? Примеры.

Контрольная работа № 1.

В ЗАДАЧАХ 1 –10 решить заданную систему уравнений, пользуясь формулами Крамера. Сделать проверку полученного решения.

1. 5x +8y-z= -7, 2. x+2y +z=4,

x+2y+3z =1, 3x-5y+3z =1,

2x-3y +2z=9. 2x +7y- z=8.

3. 3x+2y + z= 5, 4. x+2y+4z=31,

2x+3y+ z =1, 5x+ y+ 2z=29,

2x + y+3z =11. 3x –y+ z=10.

5. 4x-3y +2z=9, 6. 2x-y- z =4,

2x+5y-3z=4, 3x+4y-2z=11,

5x+6y-2z=18. 3x-2y+4z =11.

7. x+ y+2z = -1, 8. 3x-y =5,

2x-y+2z= -4, -2x+ y+ z =0,

4x+ y+ 4z= -2. 2x- y+ 4z=15.

9 . 3x –y+ z =4, 10. x+y +z =2,

2x- 5y –3z= -17, 2x- y – 6z= -1,

x + y- z= 0. 3x – 2y = 8.

В ЗАДАЧАХ 11-20 даны координаты вершин треугольника ABC. Найти: 1) длину стороны AB; 2) уравнения сторон AB и BC и их угловые коэффициенты; 3) внутренний угол B в радианах с точностью до 0,01; 4) уравнение медианы AE; 5) уравнение и длину высоты CD; 6) уравнение прямой, проходящей через точку E параллельно стороне AB.

11. A (1;-1), B (4;3), C (5;1). 12. A (0;-1), B(3,3), C(4;1).

13. A(1;-2) B (4;2), C (5;0). 14. A (2;-2), B (5;2), C (6;0).

15. A(0;0), B (3;4), C (4;2). 16. A (0;1), B (3;5), C (4;3).

17. A(3;-2), B (6;2), C (7;0). 18. A (3;-3), B (6;1), C (7;-1).

19. A (-1;1), B (2;5), C (3;3) 20. A (4;0), B(7;4), C (8;2).

В ЗАДАЧАХ 21-30 даны координаты вершин пирамиды ABCD. Требуется:

1. записать векторы в системе орт и найти модули этих векторов;

2. найти угол между векторами

3. найти проекцию вектора на вектор

4. найти площадь грани ABC;

5. найти объём пирамиды ABCD;

21. A (1;2;1), B (-1;5;1), C (-1;2;7), D (1;5;9).

22. A (2;3;2), B (0;6;2), C (0;3;8), D (2;6;10).

23. A (0;3;2), B (-2;6;2), C (-2;3;8), D (0;6;10).

24. A (2;1;2), B (0;4;2), C (0;1;8), D (2;4;10).

25. A (2;3;0), B (0;6;0), C (0;3;6), D (2;6;8).

26. A (2;2;1), B (0;5;1), C (0;2;7), D (2;5;9).

27. A (1;3;1), B (-1;6;1), C (-1;3;7), D (1;6;9).

28. A (1;2;2), B (-1;5;2), C (-1;2;8), D (1;5;10).

29. A (2;3;1), B (0;6;1), C (0;3;7), D (2;6;9).

30. A (2;2;2), B (0;5;2), C (0;2;8), D (2;5;10).

В ЗАДАЧАХ 31-40 найти указанные пределы.

31. 1) _{а) x0=2; б) x0= -1; в) x0= }

₂₎

_{32. 1) a) x0= -1; б) x0=1; в) x0=.}

₂₎

_{33. 1) а) x0=2; б) x0=-2; в) x0=.}

₂₎

_{34. 1) а) x0=1; б) x0=2; в) x0=.}

---

₂₎

_{35. 1) а) x0= -2; б) x0= -1; в)= .}

₂₎

_{36. 1) а) x0=-1; б) x0=1; в) x0=.}

₂₎

_{37. 1) a) x0=2; б) x0=-2; в) x0= }

₂₎

_{38. 1) a) x0=1; б) x0=2; в) x0=.}

₂₎

_{39. 1) а) x0= -2; б) x0= -1; в) x0=.}

₂₎

_{40. 1) a) x0= -1; б) x0=1; в) x0= .}

₂₎

_{В ЗАДАЧАХ 41-50 найти производные пользуясь правилами и формулами дифференцирования.}

_{41. а) б)}

_{в) г)}

_{42. а) б)}

_{в) г)}

_{43. а) б)}

_{в) г)}

_{44. а) б)}

_{в) г)}

_{45. а) б)}

_{в) г)}

_{46. а) б)}

_{в) г)}

_{47. а) б)}

_{в) г)}

_{48. а) б)}

_{в) г)}

_{49. а) б)}

_{в) г)}

_{50. а) б)}

_{в) г)}

_{В ЗАДАЧАХ 51-60 1). исследовать данные функции методами дифференциального исчисления и начертить их графики. 2). Для функции из пункта а) найти дополнительно наибольшее и наименьшее значения на отрезке ;.}

_{51. a) = -1; = 3;}

_б)

_{52. а) = -1; =2;}

_б)

_{53. а) =2, =4;}

_б)

_{54. а) = -1, =2;}

_б)

_{55. a) =0, =4;}

_б)

_{56. а) =-2, =3;}

_б)

_{57. а) =-3, =0;}

_б)

_{58. а) = -3, =1;}

_б)

_{59. а) =1, =4;}

_б)

_{60. а) = -1, =4;}

_б)

_{Решить ЗАДАЧИ 61-70 используя понятие экстремума функции.}

61. Каковы должны быть размеры прямоугольника наибольшей площади, вписанного в круг радиуса 6 см?

62. Проволока длиной 40 см согнута в прямоугольник. Каковы должны быть размеры этого прямоугольника, чтобы площадь его была наибольшей?

63. Найти наибольший объем цилиндра, у которого полнаяповерхность равна S=24 (м²)

64. Найти наибольший объем конуса, образующая которого равна (м).

64. Объем правильной треугольной призмы равен V= 16 (м³). Какова должна быть длина стороны основания призмы, чтобы ее полная поверхность была наименьшей?

65. Требуется изготовить ящик с крышкой, объем которого был бы равен 72 (см³), причем стороны основания относились бы как 1:2. Каковы должны быть размеры всех сторон, чтобы полная поверхность была наименьшей?

66. Требуется изготовить полотняный шатер, имеющий фор­му прямого кругового конуса заданной вместимости (м³). Каковы должны быть размеры конуса (высота и радиус основания), чтобы на шатер ушло наименьшее коли­чество полотна?

67. Найти прямоугольник наибольшей площади, если сумма длин его катета и гипотенузы постоянна и равна. 4 (см).

68. Число 8 разбить на два таких слагаемых, чтобы сумма их квадратов была наименьшей.

---

69. Число 8 разбить на два таких слагаемых, чтобы сумма ' их кубов была наименьшей.

70. Огород прямоугольной формы огорожен изгородью, дли­на которой 72 м. Каковы должны быть размеры огорода, что­бы его площадь была максимальной?

_{В ЗАДАЧАХ 71-80 найти приближённое значение функции y =f(x), заменяя приращение функции y соответствующим дифференциалом dy.}

_{71. , x=3,94}

_{72. , x=5,08}

_{73. , x= 5,84}

_{74. , x=4,06}

_{75. , x= -7,85}

_{76. , x= 9,08}

_{77. , x=1,92}

_{78. , x= 7,05}

_{79. , x= -4,03}

_{80. , x= 2,88}

_{В ЗАДАЧАХ 81-90 для кривых в указанной точке A (x1,y1) найти радиус кривизны и координаты центра кривизны.}

_{81. , 82. , A (3;4)}

_{83. y=2x}²_{, 84. A (0;1)}

_{85. , A (2;2) 86. , A(1;1)}

_{87. , A 88. , A (1;0)}

_{89. , A (1;1) 90. y =cosx , .}

---

---