ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 52
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Сидоров) Хор. инж. (Сидоров )
П2: Безграм. чел-к (Сидоров)
Отрицание Теоремы:
Хор. инж. (Сидоров )
Доказательство:
П 1а: Безграм. чел-к (Сидоров) Хор. инж. (Сидоров ) =
1а: Безграм. чел-к (Сидоров) Хор. инж. (Сидоров ) =


= Безграм. чел-к (Сидоров) Хор. инж. (Сидоров )
П2: Безграм. чел-к (Сидоров)

Хор. инж. (Сидоров )


T: Хор. инж. (Сидоров ) противоречие
Теорема доказана
……………………………………………………………………………………………..
ЗАДАЧА ИП-2(«Платон»)
Доказать теорему "прямым" методом и методом резолюции:
- Все люди разумны.
- Платон – человек.
Следовательно, Платон – разумен.
…………………….. Прямое доказательство…………….
Посылки:
П1: х (ЧЕЛОВЕК (х) РАЗУМЕН(х ) )
П2: ЧЕЛОВЕК (Платон)
Теорема: РАЗУМЕН (Платон )
1. Применить к П 1 правило специализации
Х Р(Х)
 Р(А) положив Х = Платон
Р(А) положив Х = Платон
Получим:
П1а: ЧЕЛОВЕК (Платон) РАЗУМЕН(Платон )
П2: ЧЕЛОВЕК (Платон)
2. Применить к П2 и П1а ModusPonens: P, PQ
Q
ЧЕЛОВЕК (Платон), ЧЕЛОВЕК (Платон) РАЗУМЕН(Платон )
РАЗУМЕН(Платон )
………Доказательство методом резолюции …………….
После применения правила специализации :
П1а: ЧЕЛОВЕК (Платон) РАЗУМЕН(Платон )
П2: ЧЕЛОВЕК (Платон)
О трицание теоремы: РАЗУМЕН (
трицание теоремы: РАЗУМЕН (
Платон )
П1а: ЧЕЛОВЕК (Платон) РАЗУМЕН(Платон ) =

= ЧЕЛОВЕК (Платон) РАЗУМЕН(Платон )
П
 2: ЧЕЛОВЕК (Платон) РАЗУМЕН(Платон )
2: ЧЕЛОВЕК (Платон) РАЗУМЕН(Платон )


 Т: РАЗУМЕН (Платон )
Т: РАЗУМЕН (Платон )
Теорема доказана
……………………………………………………………………….
ЗАДАЧА ИП-3(«Спортсмен») (МЭИ - ИП/17 с. 35)Не закончено!
Доказать теорему методом резолюции:
- П1: Каждый спортсмен – силен.
- П2: Каждый, кто силен и интеллигентен, добьется в жизни
успеха.
- П3: Петр – спортсмен и интеллигентен.
Теорема
Т: Следовательно, Петр добьется в жизни успеха.
......................................................................................................
РЕШЕНИЕ
Введем предикаты:
СПОРТСМЕН (х) - " х - спортсмен"
СИЛЬНЫЙ (х ) - "х - сильный человек"
ИНТЕЛЛИГЕНТНЫЙ (х) - " х - интеллигентный человек"
УСПЕХ(х) - "х добьется успеха"
ПОСЫЛКИ:
П1: х (СПОРТСМЕН (х) СИЛЬНЫЙ (х ) )
П2: х (СИЛЬНЫЙ (х) ИНТЕЛЛИГЕНТНЫЙ (х)
УСПЕХ (х) )
П3: СПОРТСМЕН (Петр) ИНТЕЛЛИГЕНТНЫЙ (Петр)
ТЕОРЕМА
Т: УСПЕХ (Петр) - "Петр добьется успеха"
Доказательство методом резолюции
1. Применить правило СПЕЦИАЛИЗАЦИИ к посылкам П1 и П2, положив
х = Петр. Получим:
П1: СПОРТСМЕН (Петр) СИЛЬНЫЙ (Петр)
П2: СИЛЬНЫЙ (Петр) ИНТЕЛЛИГЕНТНЫЙ (Петр)
УСПЕХ (Петр)
П3: СПОРТСМЕН (Петр) ИНТЕЛЛИГЕНТНЫЙ (Петр)
ТЕОРЕМА Т: УСПЕХ (Петр) - "Петр добьется успеха"
Доказательство методом резолюции
1. Применить правило СПЕЦИАЛИЗАЦИИ к посылкам П1 и П2, положив
х = Петр. Получим:
П1: СПОРТСМЕН (Петр) СИЛЬНЫЙ (Петр)
П2: СИЛЬНЫЙ (Петр)
ИНТЕЛЛИГЕНТНЫЙ (Петр)
УСПЕХ (Петр)
П3: СПОРТСМЕН (Петр) ИНТЕЛЛИГЕНТНЫЙ (Петр)
ТЕОРЕМА Т: УСПЕХ (Петр)
ЗАКОНЧИТЬ
…………………………………………………………
ЗАДАЧА ИП-8
Доказать теорему методом резолюции (и "прямым" методом ):
- Каждый философ – мудрец.
- Каждый, кто является мудрецом и обладает интуицией, может предсказать будущее.
- Сенека – философ и обладает интуицией.
Следовательно, Сенека может предсказать будущее.
(см. Прилагаемое решение)
………………………………………………………………………………………………….
ЗАДАЧА ИП-9(а,б) («Современный компьютер»)
Доказать теорему (варианты (а) и (б)) "прямым" методом и методом резолюции:
ЗАДАЧА ИП-9(а)
- Ни один современный компьютер не является механическим вычислительным устройством.
- Блок А-85 – механическое вычислительное устройство
Следовательно: Блок А-85 не является современным компьютером
Предикаты: Мех_устр-во (х) - "х – механич. вычисл-е устройство"
Совр_комп-р (х) - "х – современный компьютер"
Посылки:
П 1: х ( Совр_комп-р(х) Мех_устр-во (х) )
1: х ( Совр_комп-р(х) Мех_устр-во (х) )
П2: Мех_устр-во (А-85)
Т еорема Т: Совр_комп-р (А-85)
еорема Т: Совр_комп-р (А-85)
Прямой метод
1. Применить правило специализации к посылке П1, положив х = А-85:
П 1а: Совр_комп-р(А-85) Мех_устр-во (А-85)
1а: Совр_комп-р(А-85) Мех_устр-во (А-85)
П2: Мех_устр-во (А-85)
2. Применить к П2 и П1а правило
Modus Tollendo Tolltns: P Q, Q
P
где : P = Совр_комп-р(А-85)

Q = Мех_устр-во (А-85)
( Совр_комп-р(А-85)Мех_устр-во (А-85)), Мех_устр-во (А-85)
Совр_комп-р(А-85)Мех_устр-во (А-85)), Мех_устр-во (А-85)

Совр_комп-р(А-85)
Т еорема Т: Совр_комп-р (А-85) - доказана.
еорема Т: Совр_комп-р (А-85) - доказана.
………………………………………………………………………………….
Правило резолюции
применить
к посылкам П1а, П2 и отрицанию теоремы:
П 1а: Совр_комп-р(А-85) Мех_устр-во (А-85) =
1а: Совр_комп-р(А-85) Мех_устр-во (А-85) =

 = Совр_комп-р(А-85) Мех_устр-во (А-85)
= Совр_комп-р(А-85) Мех_устр-во (А-85)

П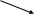 2: Мех_устр-во (А-85) Совр_комп-р(А-85)
2: Мех_устр-во (А-85) Совр_комп-р(А-85)

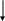
Т еорема Т: Совр_комп-р (А-85)
еорема Т: Совр_комп-р (А-85)
противоречие
Теорема доказана
……………………………………………………………………………………………………
ЗАДАЧА ИП-9 (б)
- Ни одно механическое устройство не является современным компьютером.
-Арифмометр "Альфа" – механическое вычислительное устройство
Следовательно, арифмометр "Альфа" не является современным компьютером
Предикаты: Мех_устр-во (х) - "х – механич. вычисл-е устройство"
Совр_комп-р (х) - "х – современный компьютер"
П осылки:
осылки:
П1: х (Мех_устр-во (х) Совр_комп-р(х) )
П2: Мех_устр-во (Альфа)
Т еорема Т: Совр_комп-р (Альфа)
еорема Т: Совр_комп-р (Альфа)
Прямой метод
1. Применить правило специализации к посылке П1, положив х = Альфа:
П 1а: Мех_устр-во (Альфа) Совр_комп-р(Альфа)
1а: Мех_устр-во (Альфа) Совр_комп-р(Альфа)
П2: Мех_устр-во (Альфа)
2. Применить к П2 и П1а правило ModusPonens:
P, P Q
Q
где : P = Мех_устр-во (Альфа)

Q = Совр_комп-р(Альфа)

(Мех_устр-во (Альфа),((Мех_устр-во (Альфа)Совр_комп-р( Альфа))

Совр_комп-р( Альфа)
Т еорема Т: Совр_комп-р (Альфа) - доказана.
еорема Т: Совр_комп-р (Альфа) - доказана.
………………………………………………………………………………….
Правило резолюции
к посылкам П1а, П2 и отриц. теоремы:
П 1а: Мех_устр-во (Альфа) Совр_комп-р(Альфа)
1а: Мех_устр-во (Альфа) Совр_комп-р(Альфа)
П2: Мех_устр-во (Альфа)
Т : Совр_комп-р (Альфа)


М ех_устр-во (Альфа) Совр_комп-р(Альфа)
ех_устр-во (Альфа) Совр_комп-р(Альфа)
М
 ех_устр-во (Альфа)
ех_устр-во (Альфа)
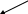 Совр_комп-р(Альфа)
Совр_комп-р(Альфа)
С овр_комп-р (Альфа)
овр_комп-р (Альфа)
противоречие
Теорема доказана
………………………………………………………………………………………………….
ЗАДАЧА ИП-10 «Аэростат»
Доказать теорему методом резолюции :
(Док-во прямым методом - неясно )
П1 - Все летательные аппараты, которые тяжелее воздуха, имеют
двигатель или крылья
П2 - Аэростат – летательный аппарат
П3 - Аэростат не имеет ни двигателя, ни крыльев
(не имеет двигателя и не имеет крыльев)
..............................................................................................
Т: Следовательно, аэростат не тяжелее воздуха
РЕШЕНИЕ
ПРЕДИКАТЫ:
ЛА (Х) - "Х – летательный аппарат"
ИД (Х) - " Х имеет двигатель"
ИК(Х) - " Х имеет крылья"
ТВ(Х) - "Х – тяжелее воздуха"
Посылки
П1: Х ( ЛА(Х) ТВ(Х) ИД(Х) ИК(Х) )
П2: ЛА (Аэростат)


П3: ИД (Аэростат) ИК (Аэростат)
Теорема

Т: ТВ (Аэростат)
РЕШЕНИЕ
1. Применить к Посылке1 правило "Специализации"
Х Р(Х)
 Р(А) положив Х = Аэростат = Аэр.
Р(А) положив Х = Аэростат = Аэр.
П1: ЛА(Аэр)ТВ(Аэр) ИД(Аэр) ИК(Аэр)
П2: ЛА(Аэр)
П2: Безграм. чел-к (Сидоров)
Отрицание Теоремы:
Хор. инж. (Сидоров )
Доказательство:
П
 1а: Безграм. чел-к (Сидоров) Хор. инж. (Сидоров ) =
1а: Безграм. чел-к (Сидоров) Хор. инж. (Сидоров ) = 

= Безграм. чел-к (Сидоров) Хор. инж. (Сидоров )
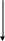
П2: Безграм. чел-к (Сидоров)

Хор. инж. (Сидоров )


T: Хор. инж. (Сидоров ) противоречие
Теорема доказана
……………………………………………………………………………………………..
ЗАДАЧА ИП-2(«Платон»)
Доказать теорему "прямым" методом и методом резолюции:
- Все люди разумны.
- Платон – человек.
Следовательно, Платон – разумен.
…………………….. Прямое доказательство…………….
Посылки:
П1: х (ЧЕЛОВЕК (х) РАЗУМЕН(х ) )
П2: ЧЕЛОВЕК (Платон)
Теорема: РАЗУМЕН (Платон )
1. Применить к П 1 правило специализации
Х Р(Х)
 Р(А) положив Х = Платон
Р(А) положив Х = ПлатонПолучим:
П1а: ЧЕЛОВЕК (Платон) РАЗУМЕН(Платон )
П2: ЧЕЛОВЕК (Платон)
2. Применить к П2 и П1а ModusPonens: P, PQ
Q
ЧЕЛОВЕК (Платон), ЧЕЛОВЕК (Платон) РАЗУМЕН(Платон )
РАЗУМЕН(Платон )
………Доказательство методом резолюции …………….
После применения правила специализации :
П1а: ЧЕЛОВЕК (Платон) РАЗУМЕН(Платон )
П2: ЧЕЛОВЕК (Платон)
О
 трицание теоремы: РАЗУМЕН (
трицание теоремы: РАЗУМЕН (
Платон )
П1а: ЧЕЛОВЕК (Платон) РАЗУМЕН(Платон ) =

= ЧЕЛОВЕК (Платон) РАЗУМЕН(Платон )
П
 2: ЧЕЛОВЕК (Платон) РАЗУМЕН(Платон )
2: ЧЕЛОВЕК (Платон) РАЗУМЕН(Платон )

 Т: РАЗУМЕН (Платон )
Т: РАЗУМЕН (Платон )
Теорема доказана
……………………………………………………………………….
ЗАДАЧА ИП-3(«Спортсмен») (МЭИ - ИП/17 с. 35)Не закончено!
Доказать теорему методом резолюции:
- П1: Каждый спортсмен – силен.
- П2: Каждый, кто силен и интеллигентен, добьется в жизни
успеха.
- П3: Петр – спортсмен и интеллигентен.
Теорема
Т: Следовательно, Петр добьется в жизни успеха.
......................................................................................................
РЕШЕНИЕ
Введем предикаты:
СПОРТСМЕН (х) - " х - спортсмен"
СИЛЬНЫЙ (х ) - "х - сильный человек"
ИНТЕЛЛИГЕНТНЫЙ (х) - " х - интеллигентный человек"
УСПЕХ(х) - "х добьется успеха"
ПОСЫЛКИ:
П1: х (СПОРТСМЕН (х) СИЛЬНЫЙ (х ) )
П2: х (СИЛЬНЫЙ (х) ИНТЕЛЛИГЕНТНЫЙ (х)
УСПЕХ (х) )
П3: СПОРТСМЕН (Петр) ИНТЕЛЛИГЕНТНЫЙ (Петр)
ТЕОРЕМА
Т: УСПЕХ (Петр) - "Петр добьется успеха"
Доказательство методом резолюции
1. Применить правило СПЕЦИАЛИЗАЦИИ к посылкам П1 и П2, положив
х = Петр. Получим:
П1: СПОРТСМЕН (Петр) СИЛЬНЫЙ (Петр)
П2: СИЛЬНЫЙ (Петр) ИНТЕЛЛИГЕНТНЫЙ (Петр)
УСПЕХ (Петр)
П3: СПОРТСМЕН (Петр) ИНТЕЛЛИГЕНТНЫЙ (Петр)
ТЕОРЕМА Т: УСПЕХ (Петр) - "Петр добьется успеха"
Доказательство методом резолюции
1. Применить правило СПЕЦИАЛИЗАЦИИ к посылкам П1 и П2, положив
х = Петр. Получим:
П1: СПОРТСМЕН (Петр) СИЛЬНЫЙ (Петр)
П2: СИЛЬНЫЙ (Петр)
ИНТЕЛЛИГЕНТНЫЙ (Петр)
УСПЕХ (Петр)
П3: СПОРТСМЕН (Петр) ИНТЕЛЛИГЕНТНЫЙ (Петр)
ТЕОРЕМА Т: УСПЕХ (Петр)
ЗАКОНЧИТЬ
…………………………………………………………
ЗАДАЧА ИП-8
Доказать теорему методом резолюции (и "прямым" методом ):
- Каждый философ – мудрец.
- Каждый, кто является мудрецом и обладает интуицией, может предсказать будущее.
- Сенека – философ и обладает интуицией.
Следовательно, Сенека может предсказать будущее.
(см. Прилагаемое решение)
………………………………………………………………………………………………….
ЗАДАЧА ИП-9(а,б) («Современный компьютер»)
Доказать теорему (варианты (а) и (б)) "прямым" методом и методом резолюции:
ЗАДАЧА ИП-9(а)
- Ни один современный компьютер не является механическим вычислительным устройством.
- Блок А-85 – механическое вычислительное устройство
Следовательно: Блок А-85 не является современным компьютером
Предикаты: Мех_устр-во (х) - "х – механич. вычисл-е устройство"
Совр_комп-р (х) - "х – современный компьютер"
Посылки:
П
 1: х ( Совр_комп-р(х) Мех_устр-во (х) )
1: х ( Совр_комп-р(х) Мех_устр-во (х) )П2: Мех_устр-во (А-85)
Т
 еорема Т: Совр_комп-р (А-85)
еорема Т: Совр_комп-р (А-85) Прямой метод
1. Применить правило специализации к посылке П1, положив х = А-85:
П
 1а: Совр_комп-р(А-85) Мех_устр-во (А-85)
1а: Совр_комп-р(А-85) Мех_устр-во (А-85) П2: Мех_устр-во (А-85)
2. Применить к П2 и П1а правило
Modus Tollendo Tolltns: P Q, Q
P
где : P = Совр_комп-р(А-85)

Q = Мех_устр-во (А-85)
(
 Совр_комп-р(А-85)Мех_устр-во (А-85)), Мех_устр-во (А-85)
Совр_комп-р(А-85)Мех_устр-во (А-85)), Мех_устр-во (А-85)
Совр_комп-р(А-85)
Т
 еорема Т: Совр_комп-р (А-85) - доказана.
еорема Т: Совр_комп-р (А-85) - доказана.………………………………………………………………………………….
Правило резолюции
применить
к посылкам П1а, П2 и отрицанию теоремы:
П
 1а: Совр_комп-р(А-85) Мех_устр-во (А-85) =
1а: Совр_комп-р(А-85) Мех_устр-во (А-85) = 
 = Совр_комп-р(А-85) Мех_устр-во (А-85)
= Совр_комп-р(А-85) Мех_устр-во (А-85)

П
 2: Мех_устр-во (А-85) Совр_комп-р(А-85)
2: Мех_устр-во (А-85) Совр_комп-р(А-85) 
Т
 еорема Т: Совр_комп-р (А-85)
еорема Т: Совр_комп-р (А-85) противоречие
Теорема доказана
……………………………………………………………………………………………………
ЗАДАЧА ИП-9 (б)
- Ни одно механическое устройство не является современным компьютером.
-Арифмометр "Альфа" – механическое вычислительное устройство
Следовательно, арифмометр "Альфа" не является современным компьютером
Предикаты: Мех_устр-во (х) - "х – механич. вычисл-е устройство"
Совр_комп-р (х) - "х – современный компьютер"
П
 осылки:
осылки:П1: х (Мех_устр-во (х) Совр_комп-р(х) )
П2: Мех_устр-во (Альфа)
Т
 еорема Т: Совр_комп-р (Альфа)
еорема Т: Совр_комп-р (Альфа) Прямой метод
1. Применить правило специализации к посылке П1, положив х = Альфа:
П
 1а: Мех_устр-во (Альфа) Совр_комп-р(Альфа)
1а: Мех_устр-во (Альфа) Совр_комп-р(Альфа) П2: Мех_устр-во (Альфа)
2. Применить к П2 и П1а правило ModusPonens:
P, P Q
Q
где : P = Мех_устр-во (Альфа)

Q = Совр_комп-р(Альфа)

(Мех_устр-во (Альфа),((Мех_устр-во (Альфа)Совр_комп-р( Альфа))

Совр_комп-р( Альфа)
Т
 еорема Т: Совр_комп-р (Альфа) - доказана.
еорема Т: Совр_комп-р (Альфа) - доказана.………………………………………………………………………………….
Правило резолюции
к посылкам П1а, П2 и отриц. теоремы:
П
 1а: Мех_устр-во (Альфа) Совр_комп-р(Альфа)
1а: Мех_устр-во (Альфа) Совр_комп-р(Альфа) П2: Мех_устр-во (Альфа)
Т : Совр_комп-р (Альфа)


М
 ех_устр-во (Альфа) Совр_комп-р(Альфа)
ех_устр-во (Альфа) Совр_комп-р(Альфа) М

 ех_устр-во (Альфа)
ех_устр-во (Альфа)  Совр_комп-р(Альфа)
Совр_комп-р(Альфа) С
 овр_комп-р (Альфа)
овр_комп-р (Альфа) противоречие
Теорема доказана
………………………………………………………………………………………………….
ЗАДАЧА ИП-10 «Аэростат»
Доказать теорему методом резолюции :
(Док-во прямым методом - неясно )
П1 - Все летательные аппараты, которые тяжелее воздуха, имеют
двигатель или крылья
П2 - Аэростат – летательный аппарат
П3 - Аэростат не имеет ни двигателя, ни крыльев
(не имеет двигателя и не имеет крыльев)
..............................................................................................
Т: Следовательно, аэростат не тяжелее воздуха
РЕШЕНИЕ
ПРЕДИКАТЫ:
ЛА (Х) - "Х – летательный аппарат"
ИД (Х) - " Х имеет двигатель"
ИК(Х) - " Х имеет крылья"
ТВ(Х) - "Х – тяжелее воздуха"
Посылки
П1: Х ( ЛА(Х) ТВ(Х) ИД(Х) ИК(Х) )
П2: ЛА (Аэростат)


П3: ИД (Аэростат) ИК (Аэростат)
Теорема

Т: ТВ (Аэростат)
РЕШЕНИЕ
1. Применить к Посылке1 правило "Специализации"
Х Р(Х)
 Р(А) положив Х = Аэростат = Аэр.
Р(А) положив Х = Аэростат = Аэр.П1: ЛА(Аэр)ТВ(Аэр) ИД(Аэр) ИК(Аэр)
П2: ЛА(Аэр)