П3: ИД(Аэр)  ИК(Аэр)

……………….
Т еорема Т: ТВ(Аэр)
О трицание теоремы Т: ТВ(Аэр)
2. Преобразовать посылки в конъюнктивную форму и осуществить

резолюцию соответствующих дизъюнктов:
П1: ЛА(Аэр) ТВ(Аэр)  ИД(Аэр) ИК(Аэр) =



= ЛА(Аэр) ТВ(Аэр)  ИД(Аэр) ИК(Аэр) =

= ( ЛА(Аэр)  ТВ(Аэр)  ИД(Аэр)  ИК(Аэр))
П 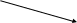2: ЛА(Аэр)

(ТВ(Аэр)  ИД(Аэр)  ИК(Аэр))






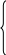
П 3: ИД(Аэр) ------------------ (ТВ(Аэр)  ИК(Аэр))





ИК(Аэр) -------------------- ТВ(Аэр)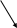







Т : ТВ(Аэр)  ДОКАЗАНО !


……………………………………………………………………………………………………

ЗАДАЧА ИП-11 (На основе ИП-3 - МЭИ - ИП/17 с. 35)

Доказать теорему методом резолюции
- Каждый врач – ответственный человек

- Каждый, кто является ответственным и знающим, заслужит признание

людей.

- Смирнов – врач и знающий человек.

Следовательно, Смирнов заслужит признание людей

…………………………………………………………………………………

Предикаты:

Врач (х) – "х- врач"

Отв_человек(х) –

---

"х- ответственный человек"

Знающий (х) - "х- знающий человек"

Заслужит_призн(х) – "х заслужит признание"

Посылки:

П1: х (Врач (х)  Отв_человек(х) )

П2: х (Отв_человек(х) & Знающий (х)  Заслужит_призн(х) )

П3: Врач(Смирнов)

П4: Знающий (Смирнов)
Теорема Т: Заслужит_призн (Смирнов)

Прямое доказательство

Применить правило специализации к П1 и П2:

П1а: Врач (Смирнов)  Отв_человек(Смирнов)

П2а: Отв_человек(Смирнов) & Знающий (Смирнов) 

 Заслужит_призн(Смирнов)

Из П1а и П3 (на осн. ModusPonens) следует

П3а : Отв_человек (Смирнов)

Из П4 и П3а следует:

П5: Знающий (Смирнов) & Отв_человек (Смирнов)
Из П5 и П2а (на осн. ModusPonens) следует:

(Знающий (Смирнов) & Отв_человек (Смирнов)),

(Знающий (Смирнов) & Отв_человек(Смирнов) & 

 Заслужит_призн(Смирнов))

Заслужит_призн(Смирнов)

Доказано:

Теорема Т: Заслужит_призн (Смирнов)

………………………………………………………………………………….

Доказательство методом резолюции

П1а: Врач (Смирнов)  Отв_человек(Смирнов) =




Врач (Смирнов)  Отв_человек(Смирнов)
П2а: Отв_человек(Смирнов) & Знающий (Смирнов) 

 Заслужит_призн(Смирнов) =

= Отв_человек(Смирнов) & Знающий (Смирнов) 

 Заслужит_призн(Смирнов) =

Отв_человек(Смирнов)  Знающий (Смирнов) 

 Заслужит_призн(Смирнов)
Итак:

Из П1а:

( Врач (Смирнов) Отв_человек(Смирнов) )

И з П2а:

(Отв_человек(Смирнов)  Знающий (Смирнов) 

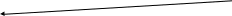 Заслужит_призн(Смирнов) )

---

( Врач (Смирнов)Знающий (Смирнов)  Заслужит_призн(Смирнов) )



(Знающий (Смирнов)  Заслужит_призн(Смирнов) П3: Врач(Смирнов)

 противоречие

П4: Знающий (Смирнов) Теорема доказана

……………………………………………………………………………
ИСКЛЮЧЕНИЕ КВАНТОРА 

путем приведения теоремы к кванторно свободной

форме

(Эти задачи в Билеты БИО-2008 не включены)
ЗАДАЧА ИП-4(«Сберкасса») МЭИ - ИП/ 2 с. 34)

Доказать теорему методом резолюции:

- Каждый, кто хранит деньги в сбербанке, получает проценты.

Следовательно, если не начисляются проценты, то никто не хранит

деньги в сбербанке.

………………………………………………………………………………………

(Использовать преобразование предикатных выражений в кванторно-свободную форму)

Решение

Введем предикаты:

хранить (х) - " х хранит деньги в сбербанке"

получать % (х) - "х получает проценты"
П осылка 1: х (хранить (х)  получать % (х))

Теорема Т: х ( получать % (х)  хранить (х) )

"Если НИКТО не получает проценты, то никто и не хранит деньги

в сбербанке.")
Получим кванторно-свободную форму этих выражений:

Посылка 1: хранить (х)  получать % (х)

Т еорема Т: получать % (х)  хранить (х)
Избавимся от импликации (А  В = А  В):

---

П 1: хранить (х)  получать % (х)

Т: получать % (х)  хранить (х)

Отрицание Теоремы:




Т: получать % (х)  хранить (х) = получать % (х) & хранить (х)

! Это два отдельных дизъюнкта

Выполним резолюцию:

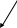П 1: хранить (х)  получать % (х) хранить (х)



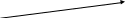Т: получать % (х) противоречие Теор. доказана

хранить (х)


ЗАДАЧА ИП-5а («Шахматисты и доминошники»(МЭИ - ИП/ 23 с. 35) -

исключение квантора 

Доказать теорему методом резолюции:

- Все, кто живет в доме № 5, заядлые шахматисты.

- Все, кто живет на соседней улице, не увлекаются шахматами..

- Все, кто НЕ живет в доме № 5,доминошники..

Следовательно, все, кто живет на соседней улице, - доминошники.

Введем предикаты:

жить_д.№5 (х) – "х живет в доме №5"

жить_сос_ул (х) - "х живет на соседней улице"

шахм (х) – "х - шахматист"

доминош (х) – "х – доминошник"

РЕШЕНИЕ

П1: х ( жить_д.№5 (х)  шахм(х) )

П 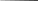2: х ( жить_сос_ул (х)  шахмат(х))

П3:х ( жить_в д.№5 (х)  доминош(х) )

……………………………………………………………………….

Т: х ( жить_сос_ул (х)  доминош(х))

Поскольку ВСЕ переменные охвачены квантором , то можно вообще исключить символы этого квантора и получить кванторно свободную форму записи в ИП.

Используем преобразование: а  в = а  в.

Получим:

П

---

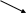1: жить_д.№5 (х)  шахм(х)

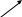
: жить_д.№5 (х) жить_сос_ул (х)

П 2: жить_сос_ул (х)  шахм(х)



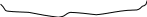жить_сос_ул (х) доминош(х)




П3: жить_д.№5 (х)  доминош(х)

……………………………………………………………………….

Т: жить_сос_ул (х)  доминош(х)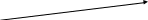

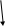доминош(х)

Т: жить_сос_ул (х) 



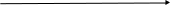доминош (х) 
ЗАДАЧА ИП-5б -Вариант Задачи 5 - исключение квантора 

- Все, кто живет в поселке "Таежный", заядлые охотники.

- Все, кто живет в г. Приозерный, не увлекаются охотой.

- Все, кто НЕ живет в поселке "Таежный", рыбаки.

Следовательно, все, кто живет в г. Приозерный, - рыбаки.

………………………………………………………………………………..
ЗАДАЧА ИП-6(МЭИ - ИП/14 с. 35)- Исключение квантора 

Доказать теорему методом резолюции:

- Все люди добры и благородны.

- Существуют легкомысленные люди.

Следовательно, существуют легкомысленные и благородные люди.

ЗАДАЧА ИП-7(МЭИ - ИП/13 с. 35 и Чень /с47, Прим. )

- Исключение кванторов  и 

Доказать теорему методом резолюции:

- Ни один торговец подержанными автомобилями не покупает подержанный автомобиль для своей семьи.

---

Смотрите также файлы

• Сидорова Тамара Григорьевна Место работы гбоу нао сш п. Харута общая информация по уроку класс укажите класс, к которому относится урок.docx

• Учебнотематический план темы Тема Количество часов теория практика 1.docx

• Профилактические мероприятия для компьютерного.docx

• В чем заключается особенность циклических движений.docx

• Функциональные особенности гипоталамогипофизарной системы, её участие в становлении репродуктивной функции человека.docx