Добавлен: 08.11.2023
Просмотров: 296
Скачиваний: 14
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1. Особенности надежности и безопасности СЖАТ
2. Показатели надёжности для невосстанавливаемых и восстанавливаемых систем
3. Методы расчета показателей надежности СЖАТ
3.1 Статистические оценки показателей надежности
3.2 Расчет надежности комбинационных схем
3.3 Расчет показателей надежности восстанавливаемых систем методом Марковских процессов
3.4 Структурный метод расчета надежности
3.5 Топологический метод расчета надежности резервированных систем
3.6 Расчет эксплуатационной надежности СЖАТ
5. Способы повышения надежности и безопасности устройств и систем ЖАТ
Статистический ряд для данной выборки, а также номер интервала, в который попадает определенное значение представлены в таблице 2.
Таблица 2
| 2928 | 3288 | 4536 | 7632 | 8448 | 10512 | 12408 | 13056 | 21336 | 25944 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 |
| 30792 | 34920 | 37200 | 37584 | 39024 | 44280 | 46344 | 51744 | 55032 | 59616 |
| 2 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 |
| 64080 | 64248 | 65712 | 66312 | 72936 | 73992 | 78912 | 79128 | 130968 | 160104 |
| 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 9 | 10 |
Возьмем диапазон значений случайной величины от 2928 до
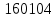 .
.Диапазон значений случайной величины t:
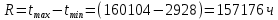
Количество интервалов K:
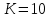
Интервал
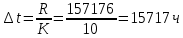
Частота попадания в i-й интервал
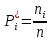
1.
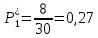
2.
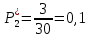
3.
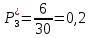
4.
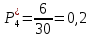
5.
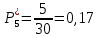
6.
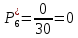
7.
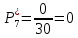
8.
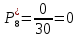
9.
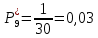
10.
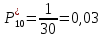
Статистическая плотность вероятности времени безотказной работы (частота отказов
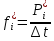
1.
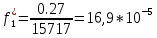
2.
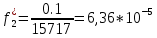
3.
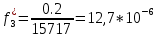
4.
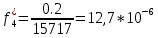
5.
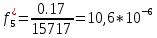
6.
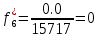
7.
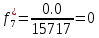
8.
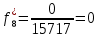
9.
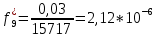
10.
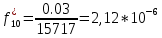
Таблица 3
| Номер интервала i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Интервал | 2928 | 18645 | 34363 | 50080 | 65798 | 81516 | 97233 | 112951 | 128668 | 144386 |
| 18645 | 34363 | 50080 | 65798 | 81516 | 97233 | 112951 | 128668 | 144386 | 160104 | |
| Длина интервала 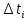 , ч , ч | 15717 | 15717 | 15717 | 15717 | 15717 | 15717 | 15717 | 15717 | 15717 | 15717 |
| Середина интервала 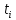 , ч , ч | 10786 | 26504 | 42222 | 57939 | 73657 | 89374 | 105092 | 120810 | 136527 | 152245 |
| Число попаданий в i-ый интервал 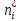 | 8 | 3 | 6 | 6 | 5 | 0 | 0 | 0 | 1 | 1 |
| Частота попадания в i-ый интервал 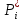 | 0,27 | 0,1 | 0,2 | 0,2 | 0,17 | 0 | 0 | 0 | 0,03 | 0,03 |
| Статистическая плотность вероятно сти 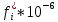 , 1/ч , 1/ч | 16,9 | 6,36 | 12,72 | 12,72 | 10,6 | 0 | 0 | 0 | 2,12 | 2,12 |
| Теоретическая плотность вероятно сти 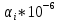 , 1/ч , 1/ч | 1,03 | 1,02 | 1,00 | 0,98 | 0,97 | 0,95 | 0,94 | 0,92 | 0,90 | 0,89 |
| Теоретическое число попаданий в i-ый интервал 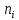 | 0,48 | 0,48 | 0,47 | 0,46 | 0,45 | 0,45 | 0,44 | 0,43 | 0,42 | 0,42 |
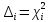 | 115,22 | 13,17 | 64,48 | 65,73 | 45,01 | 0,45 | 0,44 | 0,43 | 0,76 | 0,79 |
Построим полигон и гистограмму частот.
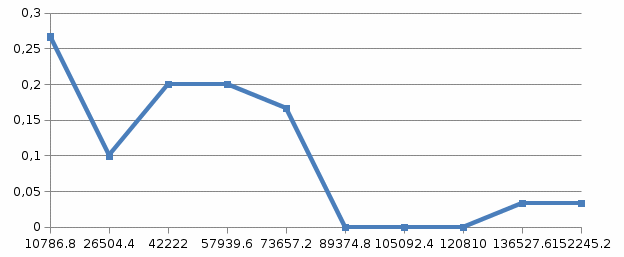
Рис. 1 График полигона (частота попадания в заданный интервал)
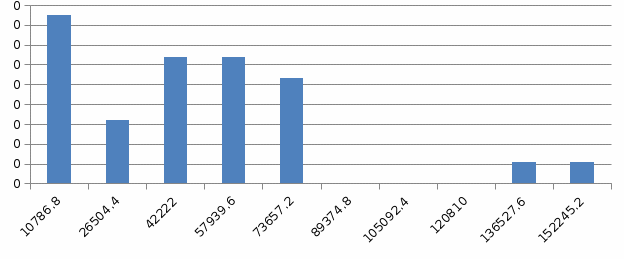
Рис. 2. Гистограмма (статистическая плотность распределения)
Построим статистическую функцию распределения Q.
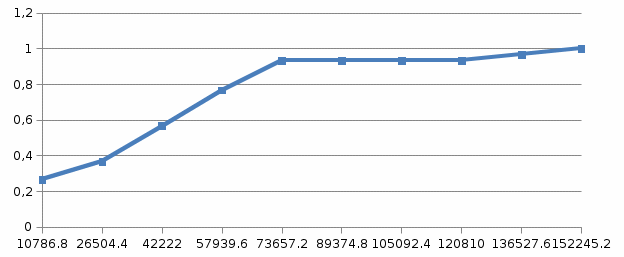
Рис. 3. Статистическая функция распределения
По виду гистограмм можно предположить экспоненциальный закон распределения времени наработки t. Примем эту гипотезу и проверим степень ее правдоподобия, используя критерий Пирсона.
Для этого построим теоретическую функцию частоты отказов, предполагая экспоненциальный закон распределения для времени наработки:
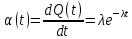 для значений ti –центров интервалов
для значений ti –центров интервалов  ti, i=1,2,3,4,5 и
ti, i=1,2,3,4,5 и 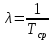
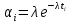
1.
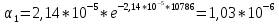
2.
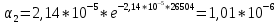
3.
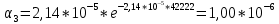
4.
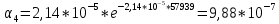
5.
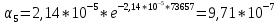
6.
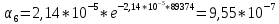
7.
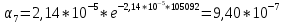
8.
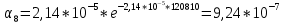
9.
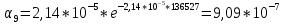
10.
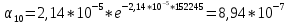
Среднее время наработки до отказа
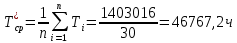
Интенсивность отказов
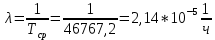
Теоретическое число попаданий в i-ый интервал:
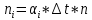
1.
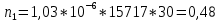
2.
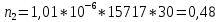
3.
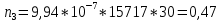
4.
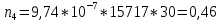
5.
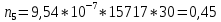
6.
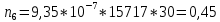
7.
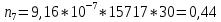
8.
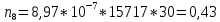
9.
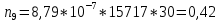
10.
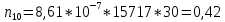
Найдем значения
 – меры расхождения между теоретическими числами
– меры расхождения между теоретическими числами  и экспериментальными
и экспериментальными  :
: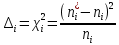
| 8 | 3 | 6 | 6 | 5 | 0 | 0 | 0 | 1 | 1 |
-
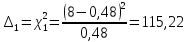
-
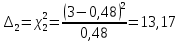
-
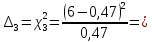 64,48
64,48 -
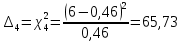
-
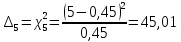
-
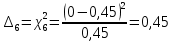
-
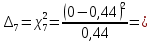 0,44
0,44 -
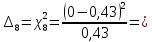 0,43
0,43 -
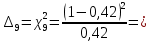 0,76
0,76 -
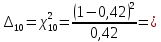 0,79
0,79
Просуммировав значения этого ряда, найдем значение
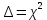 :
: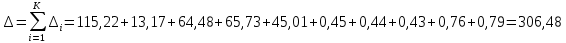
Число степеней свободы
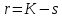 =10-1=9
=10-1=9Для r=9 и
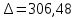
находим вероятность γ≤0,01. Это значение не превышает порог γ=0,3, что говорит о несогласии экспериментальных данных с гипотезой об экспоненциальном законе распределения времени наработки до отказа.
3.1.2 Статистическая оценка параметров надежности восстанавливаемых устройств
На предприятии в момент времени
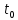 =0 было установлено
=0 было установлено 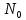 восстанавливаемых устройств. При проверках на промежутках времени
восстанавливаемых устройств. При проверках на промежутках времени 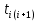 (i = 0, 1, 2) подсчитывалось, сколько устройств отказало на данном промежутке
(i = 0, 1, 2) подсчитывалось, сколько устройств отказало на данном промежутке 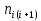 и сколько было восстановлено
и сколько было восстановлено 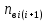 . Найти статистические параметры безотказности и ремонтопригодности на заданном промежутке времени.
. Найти статистические параметры безотказности и ремонтопригодности на заданном промежутке времени.
Рис.4.
Таблица 4
| t1 | t2 | t3 | N0 | N01 | Nв01 |
| 7 | 14 | 21 | 700 | 21 | 14 |
Вероятность безотказной работы:
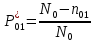 =(700-21)/700=0,97
=(700-21)/700=0,97Вероятность отказа:
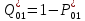 =1- 0,97=0,03
=1- 0,97=0,03Частоту отказов можно найти по формуле:
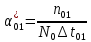 =
=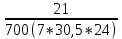 =5,85*
=5,85* 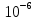 1/ч
1/чИнтенсивность отказов находим по формуле:
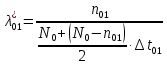 =
=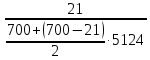 =5,94*
=5,94*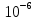 1/ч
1/ч