Добавлен: 08.11.2023
Просмотров: 291
Скачиваний: 14
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1. Особенности надежности и безопасности СЖАТ
2. Показатели надёжности для невосстанавливаемых и восстанавливаемых систем
3. Методы расчета показателей надежности СЖАТ
3.1 Статистические оценки показателей надежности
3.2 Расчет надежности комбинационных схем
3.3 Расчет показателей надежности восстанавливаемых систем методом Марковских процессов
3.4 Структурный метод расчета надежности
3.5 Топологический метод расчета надежности резервированных систем
3.6 Расчет эксплуатационной надежности СЖАТ
5. Способы повышения надежности и безопасности устройств и систем ЖАТ
Параметр потока отказов можно оценить по формуле:
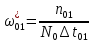 =
=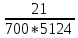 =5,85*
=5,85* 1/ч
1/чДалее найдем показатели ремонтопригодности.
Вероятность восстановления находим по формуле:
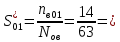 0,22
0,22Частоту восстановления и интенсивность восстановления найдем по формуле:
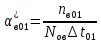 =
=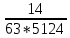 =
=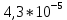 1/ч
1/ч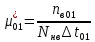 =
= 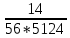 =4,88*
=4,88*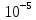 1/ч
1/ч3.2 Расчет надежности комбинационных схем
Логическая функция в алгебраическом виде:
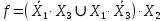
Используя правила синтеза, построим комбинационную схему на двухвходовых логических элементах:
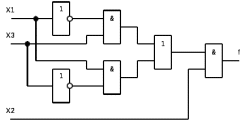
Рис.5. Комбинационная схема на логических элементах
Для анализа комбинационной схемы построим таблицу истинности:
Таблица 5
| S | X1 | X2 | X3 | f |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 |
| 3 | 0 | 1 | 1 | 1 |
| 4 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 |
| 6 | 1 | 1 | 0 | 1 |
| 7 | 1 | 1 | 1 | 0 |
Рассмотрим неисправности на выходе всех логических элементов, входящих в схему:
Таблица 6
| S | X1 | X2 | X3 | f | 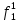 | 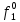 | 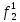 | 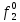 | 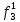 | 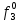 | 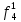 | 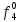 | 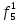 | 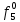 | 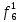 | 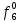 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 3 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 |
| 4 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 6 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 |
| 7 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
Произведя подобные вычисления для сбоев типа 0 1 и 1 0 всех шести элементов схемы, получим:
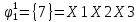 | 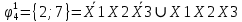 |
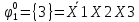 | 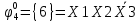 |
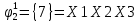 | 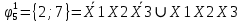 |
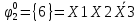 | 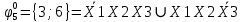 |
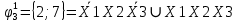 | 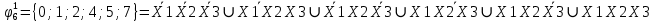 |
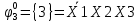 | |
| | |
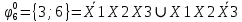 |
Вероятности появления входных переменных ????1= 0,9; ????2= 0,3; ????3= 0,6.
Определим вероятности Rk появления входных наборов и составим таблицу, отражающую полную группу событий на входе схемы:
Таблица 7
| S | X1 | X2 | X3 | f | Rk |
| 0 | 0 | 0 | 0 | 0 | 0,1*0,7*0,4=0,028 |
| 1 | 0 | 0 | 1 | 0 | 0,1*0,7*0,6=0,042 |
| 2 | 0 | 1 | 0 | 0 | 0,1*0,3*0,4=0,012 |
| 3 | 0 | 1 | 1 | 1 | 0,1*0,3*0,6=0,018 |
| 4 | 1 | 0 | 0 | 0 | 0,9*0,7*0,4=0,252 |
| 5 | 1 | 0 | 1 | 0 | 0,9*0,7*0,6=0,378 |
| 6 | 1 | 1 | 0 | 1 | 0,9*0,3*0,4=0,108 |
| 7 | 1 | 1 | 1 | 0 | 0,9*0,3*0,6=0,162 |
Вероятность истинности функции f:
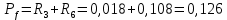
Вероятности истинности функции ошибки:
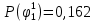 | 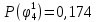 |
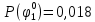 | 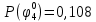 |
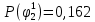 | 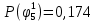 |
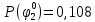 | 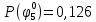 |
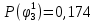 | 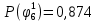 |
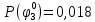 | 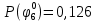 |
Вероятность появления неисправности в момент времени t для каждого элемента:
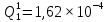 | 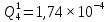 |
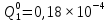 | 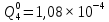 |
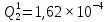 | 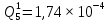 |
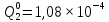 | 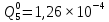 |
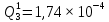 | 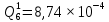 |
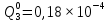 | 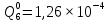 |
Вероятность ошибки на выходе схемы в момент времени t:
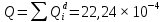
Вероятность исправной работы схемы: