Добавлен: 08.11.2023
Просмотров: 283
Скачиваний: 14
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1. Особенности надежности и безопасности СЖАТ
2. Показатели надёжности для невосстанавливаемых и восстанавливаемых систем
3. Методы расчета показателей надежности СЖАТ
3.1 Статистические оценки показателей надежности
3.2 Расчет надежности комбинационных схем
3.3 Расчет показателей надежности восстанавливаемых систем методом Марковских процессов
3.4 Структурный метод расчета надежности
3.5 Топологический метод расчета надежности резервированных систем
3.6 Расчет эксплуатационной надежности СЖАТ
5. Способы повышения надежности и безопасности устройств и систем ЖАТ
3.3 Расчет показателей надежности восстанавливаемых систем методом Марковских процессов
Исходя из значений интенсивностей отказов li и интенсивностей восстановления mi , найти параметры надежности (предполагая простейший поток отказов): финальные вероятности нахождения системы во всех состояниях Рi , в том числе вероятность отказа системы Qc ; время наработки на отказ Tcp и интенсивность отказов системы lc ; среднее время восстановления Tв; коэффициент готовности Кг ; среднее время безотказной работы системы (среднюю наработку до отказа) Тот.
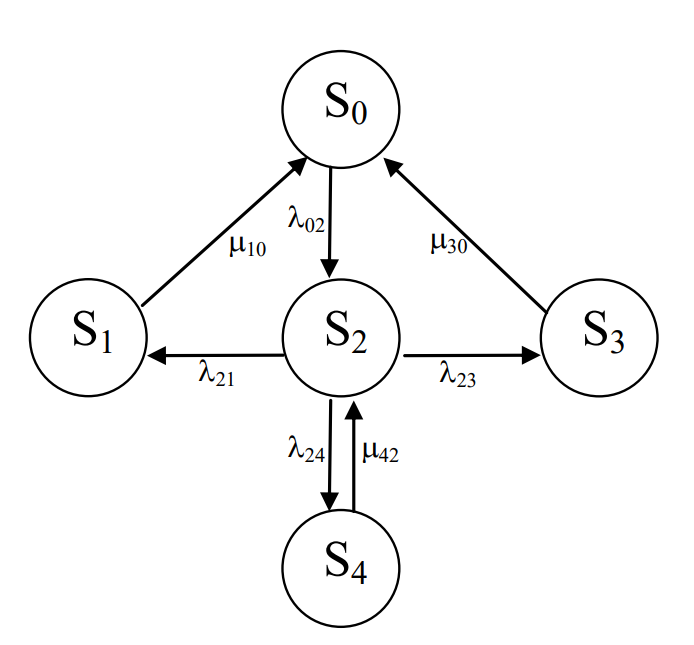
Рис.6. Граф состояний
Исходя из графа, система может находиться в одном из 5 состояний:
0 – исправное состояние;
1 – 1-е работоспособное состояние: отказал первый элемент (находится в ремонте), второй и третий – исправны;
2 - 2-е работоспособное состояние: отказал второй элемент (находится в ремонте), первый и третий – исправны;
3 – 3-е работоспособное состояние: отказал третий элемент (находится в ремонте), первый и второй – исправны;
4 – неработоспособное состояние (состояние отказа): отказали последовательно все элементы и находятся в состоянии ремонта.
Интенсивность отказов l????????=l=7∗10^−4 1/ч, интенсивность восстановления m????????=m=1,4286 1/ч.
Составим систему уравнений Колмогорова для финальных вероятностей нахождения во всех состояниях:
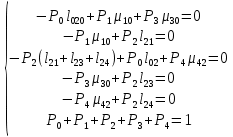
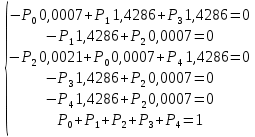
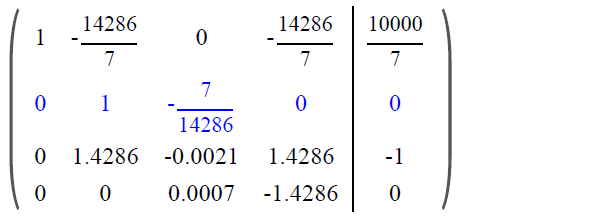
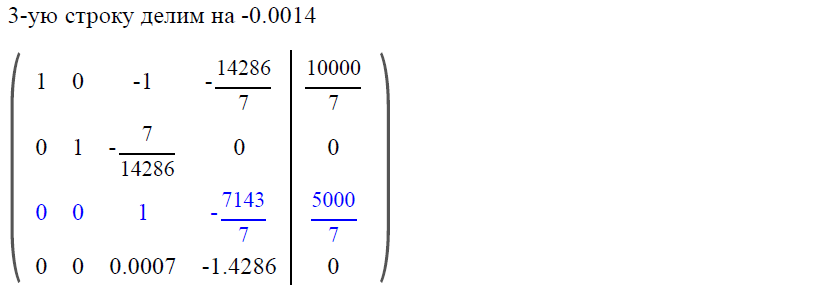
Решим систему методом Гаусса и получим значения финальных вероятностей:





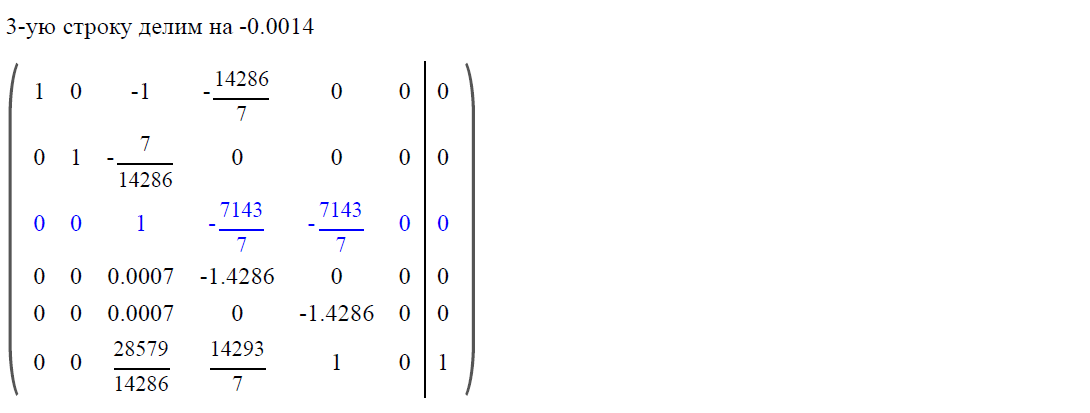







Найдем вероятность отказа системы и вероятность безотказной работы:
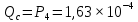
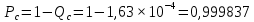
Зная финальные вероятности, найдем время наработки на отказ, интенсивность отказов системы, среднее время восстановления, коэффициент готовности:
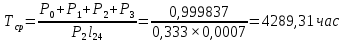
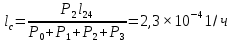
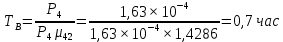
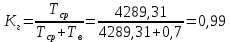
Найдём среднее время безотказной работы:
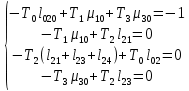
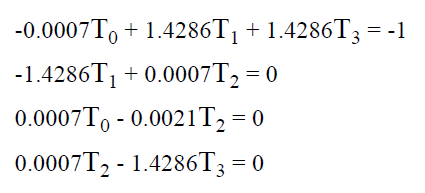







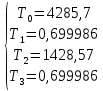
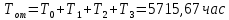
3.4 Структурный метод расчета надежности
Задана последовательно-параллельная схема расчёта надёжности. Так же задана интенсивность отказов для каждого i-ого элемента, время восстановления узла и время работы t=1год.
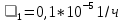 ,
, 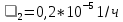 ,
, 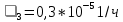 ,
, 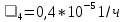 ,
, 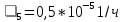 , и
, и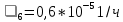 ,
, 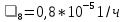 ,
, 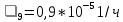
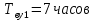 ,
, 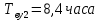 ,
, 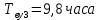

Рис.7.
Логическая функция схемы:

Арифметическая функция:
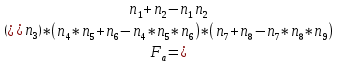
Преобразуем узлы схемы:
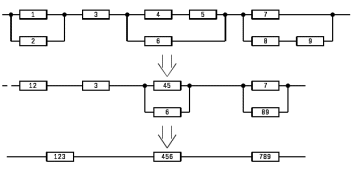
Рис.8.
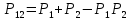
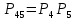
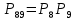
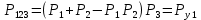
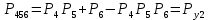
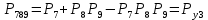
Функция надежности:
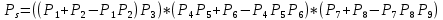
Значения функции надёжности схемы за t=1 год:
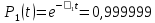
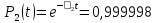
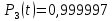
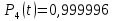
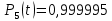
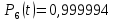
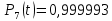
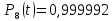
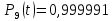
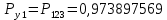
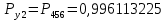
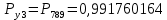
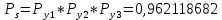
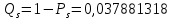
Интенсивность отказов:
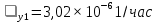
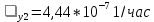
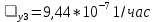
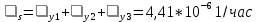
Среднее время наработки до отказа:
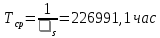
Среднее время восстановления системы:
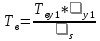 +
+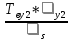 +
+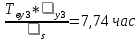
Коэффициент готовности:
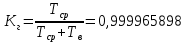
После определения всех параметров системы можно сделать вывод, что система в течение года будет работать надёжно с вероятностью 99,9966%.