Файл: Лабораторная работа Математический маятник Цель работы.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 168
Скачиваний: 7
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторная работа 1.1. Математический маятник
Цель работы: изучение гармонических колебаний, исследование зависимости периода колебаний математического маятника от его длины и определение ускорения свободного падения. Вычисление погрешностей измерений и расчётов.
Теоретическая часть
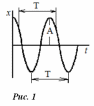
Гармоническими колебаниями физической величины х называется процесс изменения ее во времени t no закону x=Asin((2π/T)t+φo), где А – амплитуда колебаний; Т – период колебаний. Величина ((2π/T)t+φo), называется фаза колебаний, а соответствует фазе в начальный момент времени (t=0) и называется начальной фазой. График таких колебаний представлен на рис. 1. Из определения гармонических колебаний следует, что период колебаний является наименьшим промежутком времени, по истечении которого движение в точности повторяется.
 | 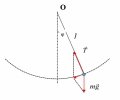 Рис.2 Рис.2 |
Амплитуда колебаний А равна максимальному значению х. Величина w, называется круговой (циклической) частотой.
Для изучения гармонических колебаний можно воспользоваться математическим маятником. Математический маятник – это (модель) идеализированная система, состоящая из материальной точки массой m, подвешенной на длинной нерастяжимой нити l, и совершающая колебания около положения равновесия.
Математический маятник при малых углах отклонения совершает гармонические колебания с циклической частотой и периодом Т.
Период колебаний маятника – это время, в течение которого маятник совершает одно полное колебание и возвращается в исходную точку.
Для определения ускорения свободного падения можно воспользоваться выражением T=2π√(l/g), откуда g=4π2((l/Т2). Чтобы рассчитать ускорение свободного падения
gпо этой формуле, достаточно измерить период колебаний Т по формуле T=t/n.
Так как g – величина постоянная для данной географической точки, то видно, что при заданной длине маятника l период колебаний маятника Т представляет собой постоянную величину. При использовании сравнительно точного прибора можно убедиться в том, что от опыта к опыту значение tизменяется то в большую, то в меньшую сторону. Различия в результатах измерения одной и той же величины объясняются случайными погрешностями. Изучение погрешностей измерений и расчётов является одной из главных целей данной лабораторной работы.
Описание экспериментальной установки
Схема экспериментальной установки и входящие в неё приборы и принадлежности приведены на рис. 3.
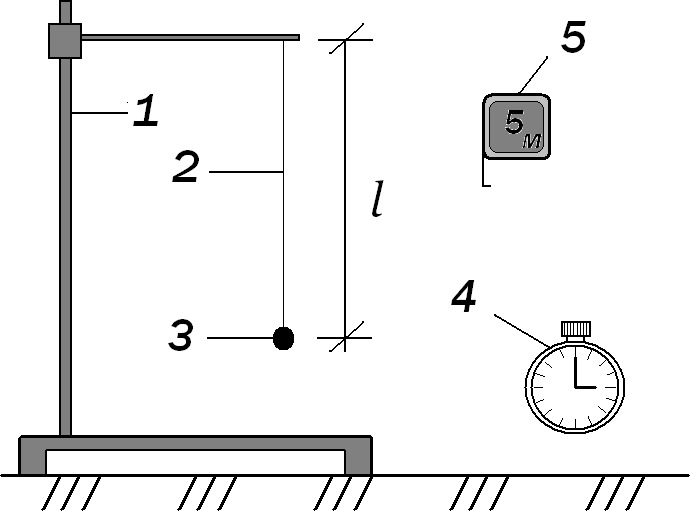
Рис. 3. Экспериментальная установка:
1 – штатив; 2 – длина маятника l; 3 – шарик; 4 – секундомер; 5 – рулетка
Первый способ. Если измерить расстояние от точки подвеса до центра тяжести шарика l, вывести из положения равновесия шарик, отклоняя его на угол 5–7°, при помощи секундомера определить время t некоторого числа n полных колебаний, затем найти период Т=t/n, то ускорение свободного падения можно определить по формуле g=4π2((l/Т2). При работе с математическим маятником имеется возможность изменять длину нити l и число колебаний n. Следует иметь в виду: при увеличении длины маятника и числа колебаний уменьшается экспериментальная погрешность.
Порядок выполнения работы
Данные на выполнение лабораторной работы:
| l =110 см | n =6 -10 | Первый способ определения ускорения свободного падения. |
Практическая часть.
Ход выполнения работы:
1.Установили заданную длину маятника l, измеряя расстояние от точки подвеса до центра масс шарика при помощи
рулетки.
2.Отклонили шарик на некоторый угол от положения равновесия. Измерили секундомером время t некоторого числа nколебаний.
Рис.4.
3.Выполнили измерения не менее пяти раз. Результаты измерений и погрешности измерительных приборов занести в таблицу 1.
4.Вычислили период колебаний для каждого измерения Т = t/n.
5.Определили ускорение свободного падения g для каждого измерения по формуле g = 4π2l/Т2
6.Вычислили среднее арифметическое ускорение свободного падения,
подставляя средние значения lсри Tср.
7.Вычислили абсолютную погрешность относительные погрешности измерения длины и периода колебаний маятника.
Погрешность измерения длины маятника определяют по цене деления рулетки, которой измеряют, а погрешность измерения периода колебаний – по методу обработки результатов прямых измерений.
Таблица 1
| i | l, см | ∆l , мм | ni | ti, с | ∆t, с | tср, с | Т, с | g, м/с2 | gср, м/с2 |
| 1 | 110 | 5 | 6 | 12,52 | 0.01 | 16,66 | 2,086 | 9,969 | 10,009=10,01 |
| 2 | 110 | 7 | 14,57 | 2,081 | 10,017 | ||||
| 3 | 110 | 8 | 16,61 | 2,076 | 10,066 | ||||
| 4 | 110 | 9 | 18,70 | 2,077 | 10,056 | ||||
| 5 | 110 | | 10 | 20,89 | 2,089 | 9,941 |
Вычисление периода колебаний и ускорения свободного падения:
Таблица 2
| Опыт 1 | T1=t1/n1=12,52/6=2,086 | g1=4π2(l/T1) = 4∙3.142∙(1.1/2,0862) ≈ 9,969 (м/с2) |
| Опыт 2 | T2=t2/n2=14,57/7=2,081 | g2=4π2(l/T2) = 4∙3.142∙(1.1/2,0812) ≈ 10,017 (м/с2) |
| Опыт 3 | T3=t3/n3=16,61/8=2,076 | g3=4π2(l/T3) = 4∙3.142∙(1.1/2,0762) ≈ 10,066 (м/с2) |
| Опыт 4 | T4=t4/n4=18,70/9=2,077 | g4=4π2(l/T4) = 4∙3.142∙(1.1/2,0772) ≈ 10,056 (м/с2) |
| Опыт 5 | T5=t5/n5=20,89/10=2,089 | g5=4π2(l/T5) = 4∙3.142∙(1.1/2,0892) ≈ 9,941 (м/с2) |
Среднее значение ускорения свободного падения:
gcp = (g1+g2+g3+g4+g5)/5 = (9,969+ 10,017+10,066+10,056+9,941)/5 = 10,009 ≈ 10,01(м/с2)
Среднее значение времени:
tср= (t1+t2+t3+t4+t5)/5 = (12,52+14,57+16,61+18,70+20,89)/5 = 16,658 ≈ 16,66 (c)
Абсолютная погрешность ускорения свободного падения

 ∆g = gср∙√(εl)2 +(2εt)2) =gср∙√(∆l/l)2 +(2∆t/tср)2 =
∆g = gср∙√(εl)2 +(2εt)2) =gср∙√(∆l/l)2 +(2∆t/tср)2 = = 10,01∙√(0,005/1,1)2 + (2∙0,01/16,66)2 = 0,047 ≈ 0,05 (м/с2)
= 10,01∙√(0,005/1,1)2 + (2∙0,01/16,66)2 = 0,047 ≈ 0,05 (м/с2)Окончательный результат:
g = gcp ± ∆g = (10,01± 0,05) м/с2
Относительная погрешность вычислений |10,01-9.81|/9.81∙100%=0.02%
Вывод: В данной лабораторной работе экспериментальным путем было определено ускорение свободного падения при помощи математического маятника. Полученные результаты имеют небольшую погрешность относительно истинного значения, что позволяет говорить о точности расчётной формулы и о незначительных погрешностях при измерениях и вычислениях.
Контрольные вопросы и ответы на них
.
Вопрос 1. Какие колебания называютсягармоническими?
Ответ: Гармонические колебания — колебания, при которых физическая величина изменяется с течением времени по гармоническому (синусоидальному) закону.
Вопрос 2. Запишите дифференциальное уравнение гармонических колебаний,его решение.
Ответ: Дифференциальное уравнение колебаний маятника имеет вид:
d2α/dt2 + w2α = 0
Решение этого уравнения имеет вид: α = αmcos(wt + φo)
Вопрос 3. Что такое математическиймаятник?
Ответ: Математический маятник – это подвешенное на невесомой нерастяжимой нити тело (материальная точка), способное под действием приложенных к нему сил совершать колебания около положения равновесия.
Вопрос 4. Запишите формулу периода колебаний математическогомаятника.
 Ответ: T=2π√l/g, где Т- период колебаний (с), l – длина математического маятника (м), g- ускорение свободного падения (м/с2).
Ответ: T=2π√l/g, где Т- период колебаний (с), l – длина математического маятника (м), g- ускорение свободного падения (м/с2).Вопрос 5. Что понимается под силой тяготения, силой тяжести и массойтела?
Ответ: Сила тяжести – это проявление закона всемирного тяготения, т.е. силы притяжения тел к Земле вблизи ее поверхности:
F = mg. Сила тяжести приложена к телу, направлена к центру Земли, и ее нужно отличать от веса тела.
Сила тяготения — сила взаимного притяжения, действующая между всеми материальными телами.
Ньютон открыл закон всемирного тяготения: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними: