Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Волгоградский государственный технический университет»
Факультет Электроники и вычислительной техники

Кафедра «Системы автоматизированного проектирования и поискового конструирования»

ОТЧЕТ


О технологической (проектно-технологической) практике
Студент гр. САПР-1.6 В ______________ Милаев О.С.

подпись
Руководитель практики ___________________ проф. Скоробогатченко Д.А.

Отчет защищен с оценкой____________


Волгоград 20____г
Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение
высшего образования

«Волгоградский государственный технический университет»

Факультет Электроники и вычислительной техники

Кафедра «Системы автоматизированного проектирования и поискового конструирования

УТВЕРЖДАЮ

Заведующий кафедрой САПРиПК

____________ д.т.н. Щербаков М.В.

(подпись) (расшифровка подписи)

«_____»________________20__г.

ЗАДАНИЕ

на технологическую (проектно-технологическую) практику
Студенту__Милаеву Олегу Сергеевичу Группа__САПР-1.6 В____

(фамилия, имя, отчество)
1.Изучить персептроны и однослойные персептронные нейронные сети.

2.Изучить модели нейрона персептрона и архитектуры персептронной однослойной нейронной сети.

3.Разработать задание для лабораторной работы.

4.Подготовить методические рекомендации по выполнению лабораторной работы по созданию моделей персептронных нейронных сетей в системе MATLAB.


Студент ________________ Милаев О.С.
Руководитель практики от ВолгГТУ: __________проф. Скоробогатченко Д.А.
Лабораторная работа №1 Персептроны и однослойные персептронные нейронные сети

Цель работы: изучение модели нейрона персептрона и архитектуры персептронной однослойной нейронной сети; создание и исследование моделей персептронных нейронных сетей в системе MATLAB.

Общие сведения

Персептроном называется простейшая нейронная сеть, веса и смещения которого могут быть настроены таким образом, чтобы решить задачу классификации входных векторов. Задачи классификации позволяют решать сложные проблемы анализа коммутационных соединений, распознавания образов и других задач классификации с высоким быстродействием и гарантией правильного результата.

Персептрон состоит из одного нейрона с настраиваемыми синаптическими весами и порогом.

Персептроны и зарождение искусственных нейронных сетей

В качестве научного предмета искусственные нейронные сети впервые заявили о себе в 40-е годы. Стремясь воспроизвести функции человеческого мозга, исследователи создали простые аппаратные модели биологического нейрона и системы его соединений. Когда нейрофизиологи достигли более глубокого понимания нервной системы человека, эти ранние попытки стали восприниматься как весьма грубые аппроксимации. Тем не менее, на этом пути были достигнуты впечатляющие результаты, стимулировавшие дальнейшие исследования, приведшие к созданию более изощренных сетей.

Первое систематическое изучение искусственных нейронных сетей было предпринято Маккалокком и Питтсом в 1943 г. Позднее в работе они исследовали сетевые парадигмы для распознавания изображений, подвергаемых сдвигам и поворотам. Простая нейронная модель, показанная на рис.1, использовалась в большей части их работы. Элемент Σ умножает каждый вход х на вес w и суммирует взвешенные входы. Если эта сумма больше заданного порогового значения, выход равен единице, в противном случае – нулю. Эти системы (и множество им подобных) получили название персептронов.Они состоят из одного слоя искусственных нейронов, соединенных с помощью весовых коэффициентов с множеством входов, хотя в принципе описываются и более сложные системы.

Розенблатт доказал замечательную теорему об обучении персептронов, объясняемую ниже. Уидроу дал ряд убедительных демонстраций систем персептронного типа, и исследователи во всем мире стремились изучить возможности этих систем. Первоначальная эйфория сменилась разочарованием, когда оказалось, что персептроны не способны обучиться решению ряда простых задач. Минский строго проанализировал эту проблему и показал, что имеются жесткие ограничения на то, что могут выполнять однослойные персептроны, и, следовательно, на то, чему они могут обучаться. Так как в то время методы обучения многослойных сетей не были известны, исследователи перешли в более многообещающие области, и исследования в области нейронных сетей пришли в упадок. Недавнее открытие методов обучения многослойных сетей в большей степени, чем какой-либо иной фактор, повлияло на возрождение интереса и исследовательских усилий.

Работа Минского, возможно, и охладила пыл энтузиастов персептрона, но обеспечила время для необходимой консолидации и развития лежащей в основе теории. Анализ Минского не был опровергнут. Он остается важным исследованием и должен изучаться, чтобы ошибки 60-х годов не повторились.

Несмотря на свои ограничения персептроны широко изучались (хотя не слишком широко использовались). Теория персептронов является основой для многих других типов искусственных нейронных сетей, и персептроны иллюстрируют важные принципы. В силу этих причин они являются логической исходной точкой для изучения искусственных нейронных сетей.

Архитектура персептрона

Нейрон, используемый в модели персептрона, имеет ступенчатую функцию активации hardlim с жесткими ограничениями (рис. 1).

Каждый элемент вектора входа персептрона взвешен с соответствующим весом w_ij, и их сумма является входом функции активации. Нейрон персептрона возвращает 1, если вход функции активации n >= 0, и 0, если n<0.



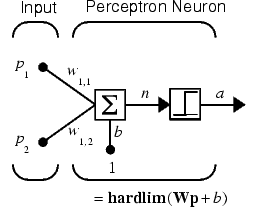
Рис. 1

Функция активации с жесткими ограничениями придает персептрону способность классифицировать векторы входа, разделяя пространство входов на 2 области, как это показано на рис. 2 для персептрона с двумя входами и смещением.



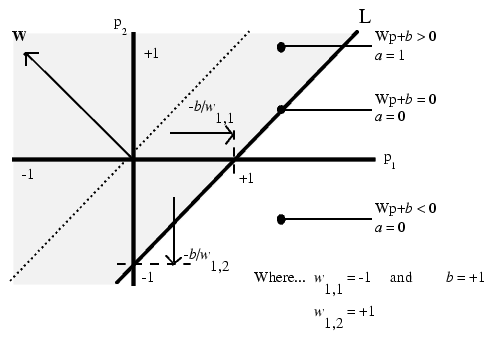
рис. 2

Пространство входов делится на 2 области разделяющей линией L, которая для двумерного случая задается уравнением

.

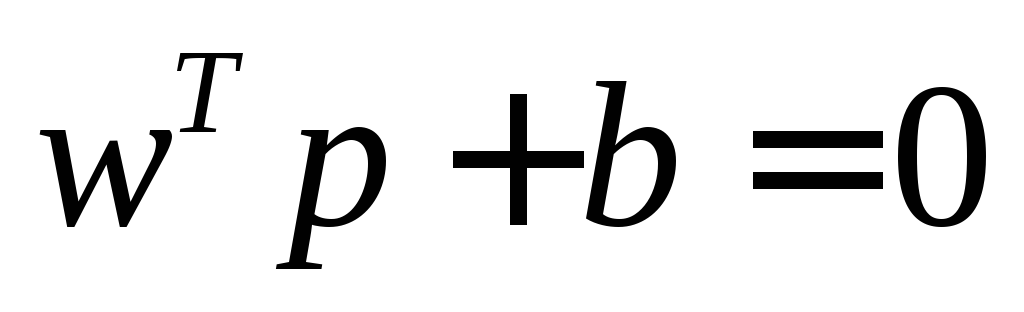Эта линия перпендикулярна к вектору весов w и смещена на величину b. Векторы входа выше линии L соответствуют положительному потенциалу нейрона, и, следовательно, выход персептрона для этих векторов будет равен 1; векторы входа ниже линии L соответствуют выходу персептрона, равному 0. При изменении значений смещения и весов граница линии L изменяет свое положение. Персептрон без смещения всегда формирует разделяющую линию, проходящую через начало координат, добавление смещения формирует линию, которая не проходит через начало координат, как это показано на рис. 2. В случае, когда размерность вектора входа превышает 2, разделяющей границей будет служить гиперплоскость.

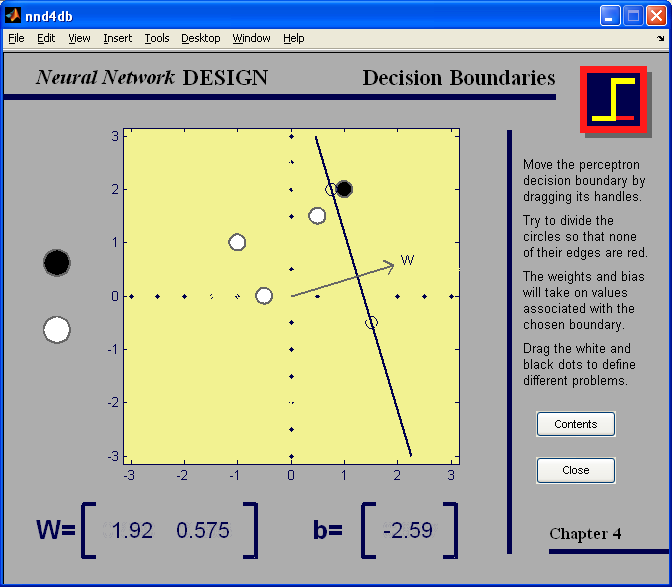
Демонстрационная программа nnd4db наглядно иллюстрирует перемещение разделяющей линии при решении задачи классификации векторов входа.



Архитектура сети

Персептрон состоит из единственного слоя, включающего S нейронов, как это показано на рис. 3 а, б в виде развернутой и укрупненной структурных схем соответственно; веса w_ij – это коэффициенты передачи от j-го входа к i-му нейрону.
Уравнение однослойного персептрона имеет вид

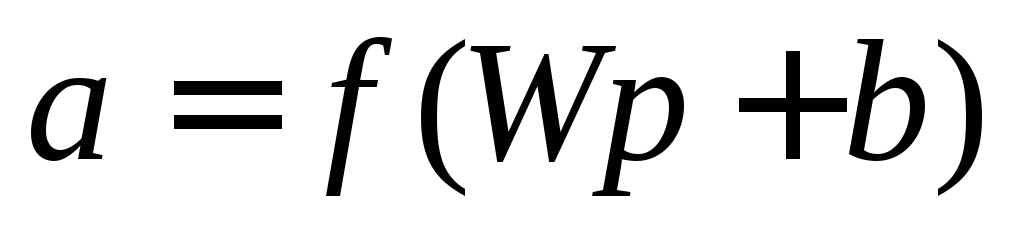. (1)



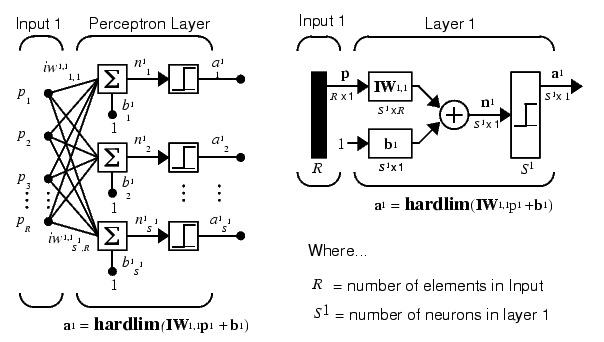
а б

Рис. 3

Обучение нейронной сети

Процесс обучения персептрона – это процедура настройки весов и смещений с целью уменьшить разность между желаемым (целевым) и истинными сигналами на его выходе, используя некоторое правило настройки (обучения).

Существует две парадигмы обучения нейронных сетей с учителем и без учителя.

С учителем (Supervised)	Без учителя (Unsupervised)
Априори известно о том, какой группе принадлежит объекты из исходного набора данных Основной механизм – подгонка параметров сети для построения аппроксимирующей функции, связывающей значения параметров объектов образующих ту или иную группу Основная цель – использование полученной модели для классификации новых образцов	Априори неизвестно существуют ли скрытые группы в данных и сколько их Основной механизм – поиск скрытых классов путем изменения пространственной топологии сети Основная цель – установить наличие групп (классов), а так же признаки или их комбинации, которые на это влияют (являются схожими для объектов той или иной группы)

---

При обучении с учителем задается множество примеров требуемого поведения сети, которое называется обучающим множеством. При подаче обучающего множества, выходы персептрона сравниваются с целями, а правило обучения используется для настройки весов и смещений персептрона так, чтобы приблизить значения выхода к целевому значению. При обучении без учителя веса и смещения изменяются только в связи с изменениями входов сети. В этом случае целевые выходы явно не задаются.

Обучение однослойного персептрона принадлежит к парадигме «Обучение с учителем».

Настройка параметров персептрона осуществляется с использованием обучающего множества. Цель обучения – уменьшить разность между реакцией нейрона и вектором цели. Для настройки персептрона применяют процедуру адаптации, которая корректирует параметры персептрона по результатам обработки каждого входного вектора. Применение функции адаптации, гарантирует, что любая задача классификации с линейно отделимыми векторами будет решена за конечное число циклов настройки. Циклом настройки называется каждая реализация процесса настройки с использованием всего обучающего множества. Ряд таких циклов и выполняется с помощью специальной функции адаптации adapt, которая при каждом цикле настройке использует обучающее множество, вычисляет выход, погрешность и выполняет подстройку параметров персептрона.

Для настройки персептрона также можно воспользоваться функцией train. Но в этом случае будет использоваться всё обучающее множество, и настройка параметров сети будет выполняться не после каждого прохода, а в результате всех проходов обучающего множества. К сожалению, не существует доказательства того, что такой алгоритм обучения персептрона является сходящимся. Поэтому использование функции train для обучения персептрона не рекомендуется.

Правило настройки персептрона должно зависеть от величины погрешности e. Вектор цели t может включать только значения 0 и 1, поскольку персептрон с функцией активации hardlim может генерировать только такие значения.

Правило настройки персептрона можно записать, связав изменение вектора весов Δw с погрешностью e = t – a:

.

Можно получить аналогичное выражение для изменения смещения, учитывая, что смещение можно рассматривать как вес для единичного входа:

---

В случае нескольких нейронов эти соотношения обобщаются следующим образом:



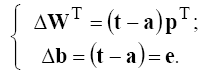
Тогда правило настройки (обучения) персептрона можно записать в следующей форме:



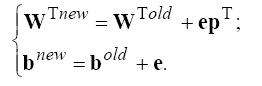
Описанные соотношения положены в основу алгоритма настройки параметров персептрона, который реализован в ППП Neural Network Toolbox в виде функции learnp. Каждый раз при выполнении функции learnp будет происходить перенастройка параметров персептрона, и, если решение существует, то процесс обучения персептрона сходится за конечное число итераций. Если смещение не используется, то функция learnp ищет решение, изменяя только вектор

весов w. Это приводит к нахождению разделяющей линии, перпендикулярной вектору w, которая должным образом разделяет векторы входа.

Рассмотрим пример обучения персептрона в ручном режиме для решения задачи классификации линейно отделимых множеств, представленных точками:





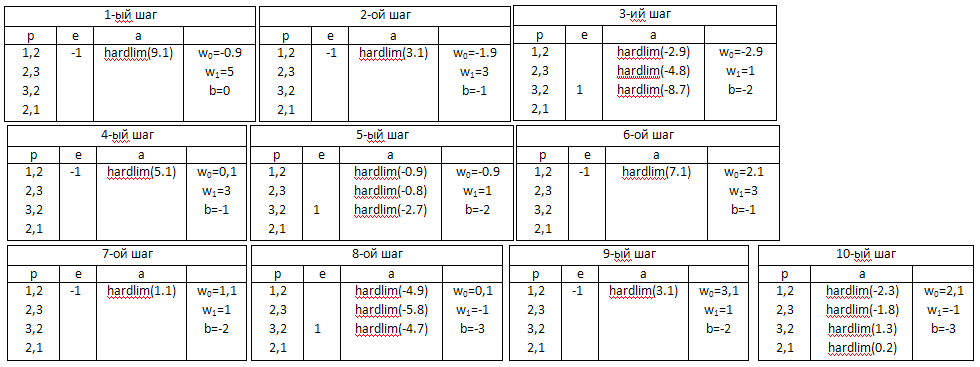
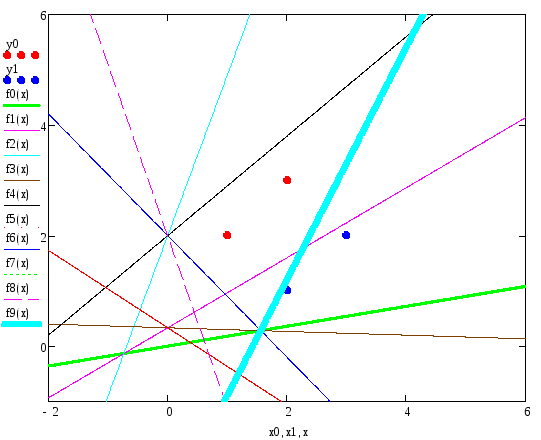
Нейронные сети на основе персептрона имеют ряд ограничений. Во-первых, выход персептрона может принимать только одно из двух значений (0 или 1, как следствие действия функции активации hardlim), иными словами, пространство входов можно разделить только на 2 области некоторой прямой линией, в многомерном случае – гиперплоскостью; во-вторых, персептроны могут решать задачи классификации только для линейно отделимых наборов векторов. Т.е. если с помощью прямой линии или гиперплоскости (в многомерном случае) можно разделить пространство входов на 2 области, в которых будут расположены векторы входа, относящиеся к различным классам, то векторы входа считаются линейно отделимыми. В противном случае процедура адаптации не в состоянии настроить персептрон так, чтобы все векторы классифицировались должным образом. Эту особенность иллюстрирует демонстрационный пример demop6, где осуществляется попытка классифицировать векторы входа, которые линейно неотделимы. В этом случае существует риск выполнения процедуры адаптации персептрона бесконечное число раз, т.к. одним из критериев останова процесса адаптации персептрона, является переход персептрона в состояние, когда его веса и смещения постоянны и уже не подвергаются коррекции. Таким образом, в случае линейно неотделимых векторов данный критерий/условие никогда не будет выполнен. Во избежание зацикливания процедуры адаптации, необходимо установить значение параметра adaptParam.passes, который указывает число совершаемых прогонов/эпох/проходов/циклов настройки, совершаемых в результате вызова процедуры адаптации. Данный параметр является вторым критерием останова процесса адаптации персептрона. Таким образом, 1-ый критерий останова адаптации персептрона будет выполнятся в случае, когда векторы входа линейно отделимы и персептрон способен их классифицировать. 2-ой критерий будет выполнятся в противном случае.

---

Модель персептрона

Для формирования модели однослойного персептрона предназначена функция newp

net = newp(PR,S)

со следующими входными аргументами: PR – массив минимальных и максимальных значений для R элементов входа размера Rx2; S – число нейронов в слое.

В качестве функции активации персептрона по умолчанию используется функция hardlim.

Моделирование персептрона

Рассмотрим однослойный персептрон с одним двухэлементным вектором входа, значения элементов которого изменяются в диапазоне -2 до 2 (p1=[-2 2], p2 = [-2 2], число нейронов в сети S =1):

clear, net = newp([-2 2; -2 2], 1);%создание персептрона net

По умолчанию веса и смещение равны нулю, и для того, чтобы установить желаемые значения, необходимо применить следующие операторы:

net.IW{1,1}=[-1 1]; % Веса w₁₁ = -1; w₁₂ = 1

net.b{1}=[1];% Смещение b = 1

Запишем уравнение (1) в развернутом виде для данной сети:



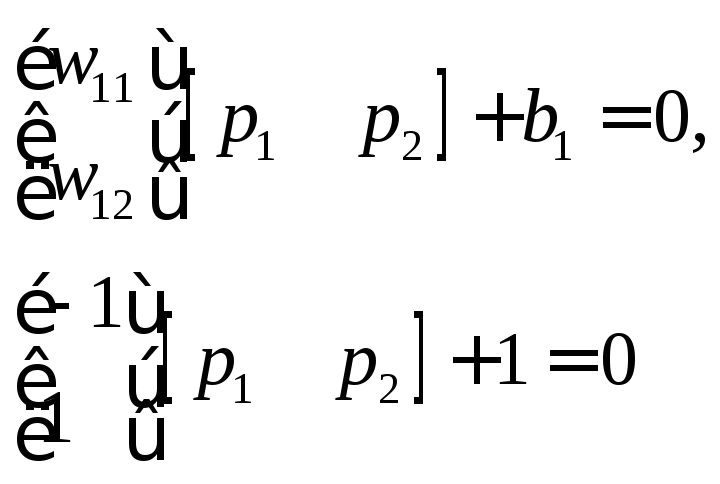
В этом случае разделяющая линия имеет вид



и соответствует линии L на рис. 2.

Определим реакцию сети на входные векторы p1 и p2, расположенные по разные стороны от разделяющей линии:

p1=[1;1];

a1=sim(net,p1)%Моделирование сети net с входным вектором p1

a1 =

1

p2=[1;-1];

a2=sim(net,p2)%Моделирование сети net с входным вектором p2

a2 =

0

Персептрон правильно классифицировал эти два вектора.

Заметим, что можно было бы ввести последовательность двух векторов в виде массива ячеек и получить результат также в виде массива ячеек

p2={[1;1] [1;-1]};

a2=sim(net,p2)

a2 =

[1] [0]

Рассмотрим наиболее значимые фрагменты кода примера demop6. Первым делом происходит инициализация переменной, содержащей двухэлементные входные вектора и переменной, содержащей вектор цели. Именно эти данные и определяют интересующую нас классификацию, с которой не может справится персептрон:

P = [ -0.5 -0.5 +0.3 -0.1 -0.8; ...

-0.5 +0.5 -0.5 +1.0 +0.0 ];

T = [1 1 0 0 0];

Далее создается однослойный персептрон с одним нейроном и задается число прогонов за выполнение процедуры адаптации:

net = newp([-40 1;-1 50],1);

net.adaptParam.passes = 3;

---

Беря во внимание указанные выше критерии останова процесса адаптации а также особенности этой процедуры, сделаем вывод о том, что следующий фрагмент кода представляет собой 75 циклов настройки персептрона, которые будут переводить его каждый раз в новое состояние, таким образом, 25 раз сработает второй критерий останова.

for a = 1:25

[net,Y,E] = adapt(net,P,T);

end;

Инициализация параметров

Для однослойного персептрона в качестве параметров нейронной сети в общем случае выступают веса входов и смещения. Допустим, что создается персептрон с двухэлементным вектором входа и одним нейроном

clear, net = newp([-2 2; -2 2], 1);

Запросим характеристики весов входа

net.inputweights{1, 1}

ans =

delays: 0

initFcn: 'initzero'

learn: 1

learnFcn: 'learnp'

learnParam: []

size: [1 2]

userdata: [1x1 struct]

weightFcn: 'dotprod'

Из этого списка следует, что в качестве функции инициализации по умолчанию используется функция initzero, которая присваивает весам входа нулевые значения. В этом можно убедиться, если извлечь значения элементов матрицы весов и смещения:

wts = net.IW{1,1}, bias = net.b{1}

wts =0 0

bias =0

Теперь переустановим значения элементов матрицы весов и смещения:

net.IW{1,1} = [3, 4]; net.b{1} = 5;

wts = net.IW{1,1}, bias = net.b{1}

wts =3 4

bias =5

Для того чтобы вернуться к первоначальным установкам параметров персептрона, предназначена функция init:

net = init(net); wts = net.IW{1,1}, bias = net.b{1}

wts =0 0

bias =0

Можно изменить способ, каким инициализируется персептрон с помощью функции init. Для этого достаточно изменить тип функций инициализации, которые применяются для установки первоначальных значений весов входов и смещений. Например, воспользуемся функцией инициализации rands, которая устанавливает случайные значения параметров персептрона:

% Задать функции инициализации весов и смещений

net.inputweights{1,1}.initFcn = 'rands';

net.biases{1}.initFcn = 'rands';

% Выполнить инициализацию ранее созданной сети с новыми функциями

net = init(net);

wts = net.IW{1,1}, bias = net.b{1}

wts =

-0.1886 0.8709

bias =

-0.6475

Видно, что веса и смещения выбраны случайным образом.

В заключение приведем код модуля, являющегося альтернативой некоторых функций nntool и предоставляющего возможность инициализации однослойного персептрона, состоящего из одного нейрона. Данный модуль был создан для проверки ручных расчетов приведенного выше примера. Входные векторы двухэлементны, а их число может быть произвольным. В модуле реализованы оба критерия останова процесса адаптации.

---

Смотрите также файлы

• Практическиориентированный государственный экзамен.docx

• Лекция Виктимология Учащийся пту 32 Афонин решил разбогатеть путем вымогательства. С этой целью он выследил шестилетнего Попкова, отправившегося гулять без сопровождения взрослых..docx

• Философия искусства.docx

• Практическое задание 2 по учебному курсу Элективные дисциплины по физической культуре и спорту.docx

• Исходя из поставленных целей, необходимо выполнить следующие задачи.docx