Государственный комитет России по связи и информатике. Московский технический университет связи и информатики. Центр дистанционного образования. Ф И З И К А (ЧАСТЬ II). Лабораторный практикум по разделу «Введение в основы электромагнетизма». Лабораторная работа №1. «Измерение горизонтальной составляющей магнитного поля Земли». Короткевич Фамилия Богдан Имя Борисович Отчество БСТ2255 Группа 22182 Номер студенческого билета

Введение.В 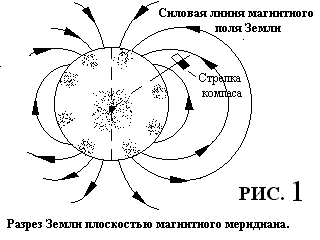работе измеряется горизонтальная составляющая магнитного поля Земли. Именно эта составляющая устанавливает в плоскости магнитного меридиана стрелку компаса с вертикальной осью вращения (рис.1).В 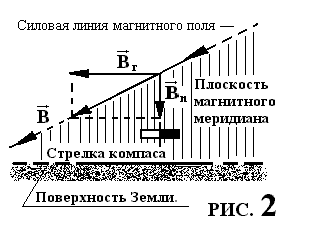близи поверхности Земли вектор индукции 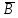(или напряжённости 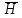) магнитного поля Земли можно разложить на две составляющие – одна направлена по нормали к поверхности Земли ( 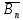), другая – параллельно ( 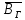) – это и есть горизонтальная составляющая (см. рис.2). Обладающая магнитным моментом 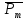стрелка компаса, помещенная в магнитное поле, испытывает действие момента силы. =[

---

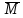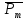
] (1)Если движение стрелки ограничено вращением относительно вертикальной оси, то в проекции на эту ось уравнение (1) даётM_z=P_mB_гsin a, (2)где а–угол между векторами и 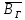.Момент (2) обращается в нуль, когда магнитный момент лежит в плоскости магнитного меридиана. Вывести стрелку из этого положения можно, создав с помощью витка с током магнитное поле 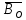, перпендикулярное плоскости магнитного меридиана. Изучая отклонения от положения а=0 под действием поля 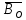можно измерить 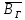.Краткая теория. Если магнитный момент , который может вращаться относительно вертикальной оси находится под действием поле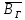й и 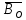, лежащих в горизонтальной плоскости, то результирующий момент, действующий на .M_z=P_mB_psin f - где 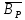– модуль результирующего поля 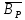= 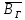+ 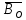, а f – угол между и 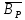. 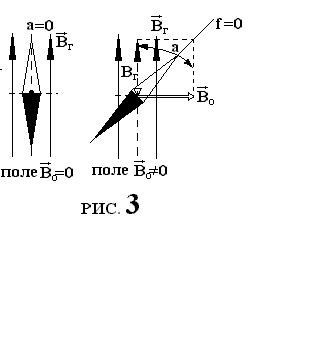В случае  , а именно такую ориентацию векторов мы имеем, если перпендикулярен плоскости магнитного меридиана,

---

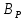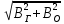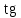
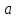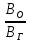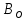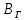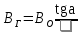
= . При этом стрелка установится так, чтобы f=0, то есть, чтобы был направлен вдоль . Новое положение соответствует повороту на угол а (см. рис. 3) относительно линий . = . Если величина созданного витком поля известна, то, измеряя угол а можно рассчитать . Для создания поля 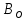в работе используется круговая рамка из N витков радиусом R, при этом в центре рамки индукция 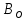определяется формулой 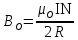,Где I – ток, текущий по виткам рамки. Таким образом 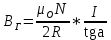.Ток I – измеряется амперметром, угол а – транспортиром (как в компасе).Доступ к работе.Вопрос 1: 50 По приведенной схеме рассчитать диапазон изменения тока, протекающего по сопротивлению R. I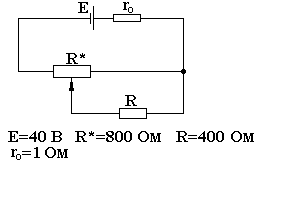_min, мА 150I_max, мА Вопрос 2:

---

1.25 *10 -7 Рассчитать индукцию магнитного поля в центре тонкой круговой катушки радиусом R=0.1 м при протекании по ней тока 0.2 А. Число витков N=100. В, Тл Практическая часть.

1. 
   Рассчитать по приведенной схеме диапазон изменения тока в рамке.
   
2. 
   О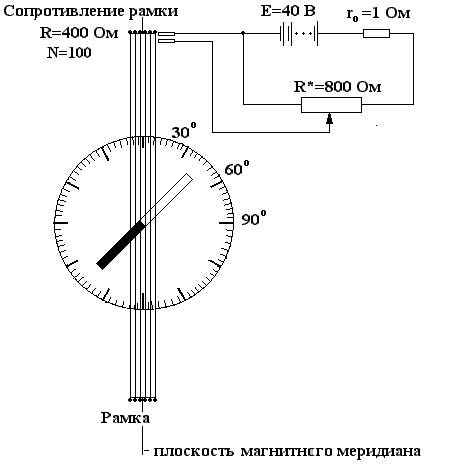 бработка результатов измерений
   

В ходе результатов измерений заполнять таблицу.

I мА	4,09	5,28	10,19	11,48	12,13
а, град	7,00	9,00	17,00	19,00	20,00
tg a	0,12	0,16	0,31	0,34	0,36
Вг	27,91	27,93	27,92	27,93	27,92

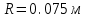
Две нижние строки таблицы заполнить, рассчитывая tga и B_г.Результат измерения В_г -6 27,922 *10 =( )

---

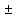Смотрите также файлы

• Курсовой проект стабилизация газового конденсата агкм голоскокова А. Ю. Группа хт0902.rtf

• Диплом Кафе 100 мест Морская Рыба.doc

• Исследование взрывчатых веществ, взрывных устройств, имитирующих их предметов и следов взрыва.rtf

• Руководство по эксплуатации Примечания Agilent Technologies, Inc., 2016.pdf

• Контрольная работа по дисциплине История Тема 5 Древняя Русь от язычества к крещению Руси и установлению православия студент 1 курса, группы атп.docx