Файл: Методические указания для студентов заочного факультета Самара 2020 10. Моменты инерции j 0.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 208
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(рис. 10). Жидкость Ж из большого закрытого резервуара, в котором поддерживается постоянный уровень, а давление на поверхности жидкости равно рм, по трубопроводу вытекает в атмосферу. Температура жидкости 200С. Диаметр трубопровода d, его горизонтальная и наклонная части одинаковой длины. Высота уровня жидкости над горизонтальной частью трубопровода равна Н, конец его наклонной части находится ниже горизонтальной части на величину h, эквивалентная шероховатость труб э=0,6 мм. Определить расход Q жидкости и построить пьезометрическую и напорную линии.
З
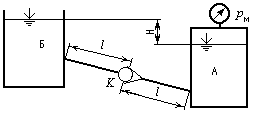
Рис. 11
адача 13 (рис. 11). Чему должно быть равно манометрическое давление рм на поверхности жидкости в закрытом резервуаре А для того, чтобы обеспечить подачу жидкости Ж в количестве Q при температуре 200С в открытый резервуар Б. Разность уровней в резервуарах Н. Трубопровод имеет длину 2l и диаметр d. Посередине его установлен обратный клапан К, коэффициент местного сопротивления которого кл., эквивалентная шероховатость труб э=0,75 мм. Построить пьезометрическую и напорную линии.
Задача 14 (рис. 12). В баке А жидкость подогревается до температуры Т0С и самотеком по трубопроводу длиной l1 попадает в производственный цех. Напор в баке А равен Н, эквивалентная шероховатость труб э=0,12 мм. Каким должен быть диаметр трубопровода, чтобы обеспечивалась подача жидкости в количестве Q при манометрическом давлении рм? Построить пьезометрическую и напорную линию.
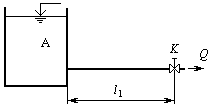
Рис. 12
3. Зависимость плотности воды от температуры
4. Давление насыщенного пара pп воды
ПРИЛОЖЕНИЯ
1. Средние значения плотности ρ и кинематической
вязкости v некоторых жидкостей
Указание. Плотность жидкости при другой температуре можно определить по формуле
Т=0/(1+∆Т), где Т-плотность жидкости при температуре Т=Т0+∆Т; ∆Т - изменение температуры; Т0 - температура, при которой плотность жидкости равна 0, - коэффициент температурного расширения жидкости (в среднем для минеральных масел можно принять =0,0007 1/оС). Стокс: Ст=см2/с=10-4 м2/с.
Задача 15 (рис. 13). Из большого открытого резервуара А, в котором поддерживается постоянный уровень жидкости, по трубопроводу, состоящему из двух последовательно соединенных труб, жидкость Ж при температуре 200С течет в резервуар Б. Разность уровней жидкости в резервуарах равна Н. Длина труб lиl2, а их диаметры d и d2, эквивалентная шероховатость труб э=0,6 мм.
Определить расход Q жидкости, протекающей пор трубопроводу. В расчетах принять, что местные потери напора составляют 15% от потерь по длине. Задачу рекомендуется решить графоаналитическим методом.
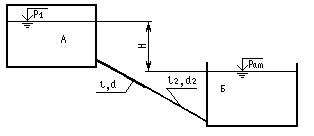
Рис. 13
Задача 16 (рис. 14). Из большого открытого резервуара А, в котором поддерживается постоянный уровень жидкости, по трубопроводу, состоящему из трех труб, длина которых l, l1, l2, а диаметры d, d1, d2, жидкость Ж при температуре 200С течет в резервуар Б. Разность уровней жидкости в резервуарах равна Н, эквивалентная шероховатость труб э=0,75 мм.
Определить: 1) расход жидкости, протекающей в резервуар Б; 2) распределение расхода жидкости между параллельно соединенными трубами 1 и 2. В расчетах принять, что местные потери напора составляют 10% от потерь по длине. Задачу рекомендуется решить графоаналитическим методом.
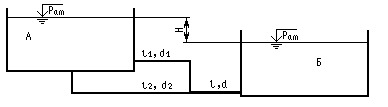
Рис. 14
Задача 17 (рис. 15). Определить расход жидкости Ж, протекающей по трубопроводу в пункты 1 и 2, если напор Н в резервуаре постоянный. Длины отдельных частей трубопровода равны l, l1, l2, а диаметры d, d1, d2; эквивалентная шероховатость труб э=0,12 мм. Температура жидкости 200С. Местные потери напора в расчетах не учитывать. Задачу рекомендуется решить графоаналитическим методом.
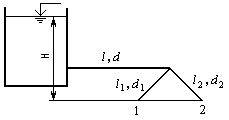
Рис. 15
Задача 18 (рис. 16). Жидкость Ж в количестве
Qтечет по горизонтальной трубе из большого резервуара А. Определить ударное повышение давления и напряжения в стенках трубы перед задвижкой К при ее внезапном закрытии. Диаметр трубы d1, ее длина l1, а толщина стенок . Температура жидкости 200С.

Рис. 16
Задача 19. По трубопроводу длиной l, диаметром d, толщиной , соединенному с баком, под напором Н течет вода (К=2.109Па). В некоторый момент времени происходит мгновенное перекрытие потока в конце трубопровода.
Найти скорость распространения волны гидравлического удара и величину ударного повышения давления, если труба стальная (Е=2.1011Па). Коэффициент гидравлического сопротивления принять равным 0,03. Как изменится ударное повышение давления, если стальную трубу заменить чугунной тех же размеров (Е=0,98.1011Па).
Задача 20 (рис 17). В бак, разделенный перегородкой на два отсека, подается жидкость Ж в количестве Q. Температура жидкости 200С. В перегородке бака имеется цилиндрический насадок, диаметр которого d, а длина l=3d. Жидкость из второго отсека через отверстие диаметра d1 поступает наружу, в атмосферу. Определить высоты Н1 и Н2 уровней жидкости. Данные для решения задачи в соответствии с вариантом задания выбрать из табл.
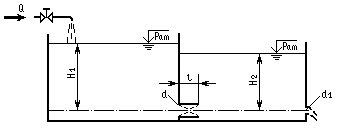
Рис. 17
Задача 21 (рис. 18). Открытый резервуар делится при помощи вертикальных перегородок на три части, сообщающиеся друг с другом. Определить расход воды через систему и найти распределение напоров Н1, Н2, и Н3, если диаметры отверстий равны d1, d2, d3 и постоянный напор Н.
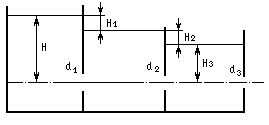
Рис. 18
Методические указания к выполнению контрольного
задания 2
Задача 1. При решении задачи применяют формулу закона внутреннего трения Ньютона. Поскольку слой масла тонкий, можно считать, что скорость в нем изменяется по прямолинейному закону.
Задача 2. При решении задачи применяют формулу закона внутреннего т рения Ньютона. Поскольку толщина слоя масла мала, можно считать, что скорость в нем меняется по прямолинейному закону. Эпюра касательных напряжений в слое масла принимается прямоугольной; сила трения проходит через центр тяжести этой эпюры.
З

Рис. 11
адача 13 (рис. 11). Чему должно быть равно манометрическое давление рм на поверхности жидкости в закрытом резервуаре А для того, чтобы обеспечить подачу жидкости Ж в количестве Q при температуре 200С в открытый резервуар Б. Разность уровней в резервуарах Н. Трубопровод имеет длину 2l и диаметр d. Посередине его установлен обратный клапан К, коэффициент местного сопротивления которого кл., эквивалентная шероховатость труб э=0,75 мм. Построить пьезометрическую и напорную линии.
Задача 14 (рис. 12). В баке А жидкость подогревается до температуры Т0С и самотеком по трубопроводу длиной l1 попадает в производственный цех. Напор в баке А равен Н, эквивалентная шероховатость труб э=0,12 мм. Каким должен быть диаметр трубопровода, чтобы обеспечивалась подача жидкости в количестве Q при манометрическом давлении рм? Построить пьезометрическую и напорную линию.

Рис. 12
-
Плотность и кинематическая вязкость воды и воздуха
(p = 98 кПа)
| Температура, 0С | , кг/м3 | 106, м2/с | , кг/м3 | 106, м2/с |
| для воды | для воздуха | |||
| 0 4 10 20 30 40 50 60 70 80 90 100 | 999,87 1000,0 999,73 998,23 995,76 992,24 998,07 983,24 997,81 971,83 965,34 953,38 | 1,79 1,65 1,31 1,01 0,81 0,60 0,56 0,48 0,42 0,37 0,33 0,29 | 1,28 1,26 1,23 1,185 1,150 1,110 1,080 1,045 1,020 0,990 0,960 0,935 | 13,7 14,1 14,7 15,7 16,6 17,6 18,6 19,6 20,45 21,7 22,9 23,8 |
3. Зависимость плотности воды от температуры
| Температура T, 0C | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Плотность , кг/м3 | 1000 | 1000 | 998 | 996 | 992 | 988 | 983 | 978 | 972 | 965 | 958 |
4. Давление насыщенного пара pп воды
| Температура T, 0C | 0,0 | 5,00 | 10,0 | 20,0 | 30,0 | 40,0 | 50,0 | 60,0 | 80,0 |
| Давление, кПа | 0,588 | 0,882 | 1,18 | 2,35 | 4,19 | 7,29 | 12,1 | 19,6 | 46,0 |
ПРИЛОЖЕНИЯ
1. Средние значения плотности ρ и кинематической
вязкости v некоторых жидкостей
| Жидкости | Плотность, кг/м3 при Т, оС | Кинематическая вязкость, Ст при Т, оС | ||||
| 20 | 50 | 20 | 40 | 60 | 80 | |
| Вода пресная Нефть Баку, легкая Нефть Баку, тяжелая Бензин авиационный Керосин Т-1(очищен.) Керосин Т-2(трактор.) Дизельное топливо Глицерин Ртуть Масла: Касторовое Трансформаторное АМГ-10 Веретенное АУ Индустриальное 12 Индустриальное 20 Индустриальное 30 Индустриальное 50 Турбинное | 998 884 924 745 808 819 846 1245 13550 960 884 - - - - - - - | - - - - - - - - - - 880 850 892 883 891 901 910 900 | 0,010 0,25 1,4 0,0073 0,025 0,010 0,28 9,7 0,0016 15 0,28 0,17 0,48 0,48 0,85 1,8 5,3 0,97 | 0,0065 - - 0,0059 0,018 - 0,12 3,3 0,0014 3,5 0,13 0,11 0,19 0,19 0,33 0,56 1,1 0,38 | 0,0047 - - 0,0049 0,012 - - 0,88 0,0010 0,88 0,078 0,085 0,098 0,098 0,14 0,21 0,38 0,16 | 0,0036 - - 0,010 - - 0,38 - 0,25 0.048 0,065 0,099 0,059 0,080 0,11 0,16 0,088 |
Указание. Плотность жидкости при другой температуре можно определить по формуле
Т=0/(1+∆Т), где Т-плотность жидкости при температуре Т=Т0+∆Т; ∆Т - изменение температуры; Т0 - температура, при которой плотность жидкости равна 0, - коэффициент температурного расширения жидкости (в среднем для минеральных масел можно принять =0,0007 1/оС). Стокс: Ст=см2/с=10-4 м2/с.
Задача 15 (рис. 13). Из большого открытого резервуара А, в котором поддерживается постоянный уровень жидкости, по трубопроводу, состоящему из двух последовательно соединенных труб, жидкость Ж при температуре 200С течет в резервуар Б. Разность уровней жидкости в резервуарах равна Н. Длина труб lиl2, а их диаметры d и d2, эквивалентная шероховатость труб э=0,6 мм.
Определить расход Q жидкости, протекающей пор трубопроводу. В расчетах принять, что местные потери напора составляют 15% от потерь по длине. Задачу рекомендуется решить графоаналитическим методом.

Рис. 13
Задача 16 (рис. 14). Из большого открытого резервуара А, в котором поддерживается постоянный уровень жидкости, по трубопроводу, состоящему из трех труб, длина которых l, l1, l2, а диаметры d, d1, d2, жидкость Ж при температуре 200С течет в резервуар Б. Разность уровней жидкости в резервуарах равна Н, эквивалентная шероховатость труб э=0,75 мм.
Определить: 1) расход жидкости, протекающей в резервуар Б; 2) распределение расхода жидкости между параллельно соединенными трубами 1 и 2. В расчетах принять, что местные потери напора составляют 10% от потерь по длине. Задачу рекомендуется решить графоаналитическим методом.

Рис. 14
Задача 17 (рис. 15). Определить расход жидкости Ж, протекающей по трубопроводу в пункты 1 и 2, если напор Н в резервуаре постоянный. Длины отдельных частей трубопровода равны l, l1, l2, а диаметры d, d1, d2; эквивалентная шероховатость труб э=0,12 мм. Температура жидкости 200С. Местные потери напора в расчетах не учитывать. Задачу рекомендуется решить графоаналитическим методом.

Рис. 15
Задача 18 (рис. 16). Жидкость Ж в количестве
Qтечет по горизонтальной трубе из большого резервуара А. Определить ударное повышение давления и напряжения в стенках трубы перед задвижкой К при ее внезапном закрытии. Диаметр трубы d1, ее длина l1, а толщина стенок . Температура жидкости 200С.

Рис. 16
Задача 19. По трубопроводу длиной l, диаметром d, толщиной , соединенному с баком, под напором Н течет вода (К=2.109Па). В некоторый момент времени происходит мгновенное перекрытие потока в конце трубопровода.
Найти скорость распространения волны гидравлического удара и величину ударного повышения давления, если труба стальная (Е=2.1011Па). Коэффициент гидравлического сопротивления принять равным 0,03. Как изменится ударное повышение давления, если стальную трубу заменить чугунной тех же размеров (Е=0,98.1011Па).
Задача 20 (рис 17). В бак, разделенный перегородкой на два отсека, подается жидкость Ж в количестве Q. Температура жидкости 200С. В перегородке бака имеется цилиндрический насадок, диаметр которого d, а длина l=3d. Жидкость из второго отсека через отверстие диаметра d1 поступает наружу, в атмосферу. Определить высоты Н1 и Н2 уровней жидкости. Данные для решения задачи в соответствии с вариантом задания выбрать из табл.

Рис. 17
Задача 21 (рис. 18). Открытый резервуар делится при помощи вертикальных перегородок на три части, сообщающиеся друг с другом. Определить расход воды через систему и найти распределение напоров Н1, Н2, и Н3, если диаметры отверстий равны d1, d2, d3 и постоянный напор Н.

Рис. 18
Методические указания к выполнению контрольного
задания 2
Задача 1. При решении задачи применяют формулу закона внутреннего трения Ньютона. Поскольку слой масла тонкий, можно считать, что скорость в нем изменяется по прямолинейному закону.
Задача 2. При решении задачи применяют формулу закона внутреннего т рения Ньютона. Поскольку толщина слоя масла мала, можно считать, что скорость в нем меняется по прямолинейному закону. Эпюра касательных напряжений в слое масла принимается прямоугольной; сила трения проходит через центр тяжести этой эпюры.