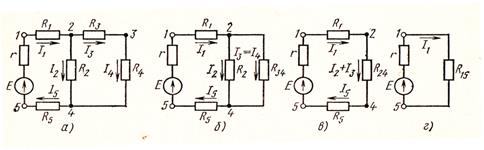
Рисунок 13. Метод свертывания цепи

Определение эквивалентных сопротивлений

Обратимся к схеме, приведенной на рисунке 13а. Сопротивления   и   соединены последовательно. Поэтому  . Эти два сопротивления можно заменить одним (эквивалентным)  , тогда схема упростится (рисунок 13б).

Сопротивления   и   включены параллельно и их можно тоже заменить одним эквивалентным:  .

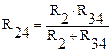Тогда схема еще упростится (рисунок 13в).

В схеме на рисунке 13в сопротивления  ,   и   включены последовательно и могут быть заменены одним эквивалентным  . Схема еще более упростится (рисунок 13г).

Подобными преобразованиями схему смешанного соединения пассивных элементов с одним источником энергии в большинстве случаев можно привести к простейшей схеме (рисунок 13г). В более сложных схемах методом эквивалентных сопротивлений достигается упрощение, которое значительно облегчает дальнейший расчет.

Определение токов

Определение начинается с простейшей схемы (рисунок 13г).

По закону Ома:   т.к.  ;  .

Зная   легко найти   и  .    .

6. 
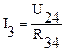   Метод контурных токов
   

Контурный ток - это величина, которая одинакова во всех ветвях данного контура.  Обычно в расчетах они обозначаются двойными индексами, например  I11, I22 и тд.

Действительный ток в определенной ветви определяется алгебраической суммой контурных токов, в которую эта ветвь входит. Нахождение действительных токов и есть первоочередная задача метода контурных токов.

Контурная ЭДС - это сумма всех ЭДС входящих в этот контур.

Собственным сопротивлением контура называется сумма сопротивлений всех ветвей, которые в него входят.

Общим сопротивлением контура называется сопротивление ветви, смежное двум контурам.

Общий план составления уравнений

1 – Выбор направления действительных токов.

2 – Выбор независимых контуров и направления контурных токов в них.

3 – Определение собственных и общих сопротивлений контуров

---

4 – Составление уравнений и нахождение контурных токов

5 – Нахождение действительных токов

7. 
   Метод узловых потенциалов
   

Метод узловых потенциалов – один из методов анализа электрической цепи, который целесообразно использовать, когда количество узлов в цепи меньше или равно числу независимых контуров. Данный метод основан на составлении уравнений по первому закону Кирхгофа. При этом, потенциал одного из узлов цепи принимается равным нулю, что позволяет сократить число уравнений до n-1.

8. 
   Метод двух узлов
   

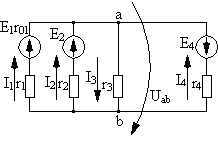
При расчете токов методом двух узлов вначале определяют напряжение между узлами, а затем по закону Ома для участка цепи находят токи в ветвях. Для схемы (рис. 6) заданы параметры элементов:

r ₁= 2 Ом,r₀₁= 0,5 Ом,

E₁= 100 В,r₂= 4 Ом,

E₂= 40 В, r₃= 5 Ом,

E₄= 10 В,r₄= 20 Ом.

Рис. 6

Определить токи во всех ветвях методом двух узлов.

Порядок расчета:

А.Выбираем условное положительное направление напряжения, например, от узла «a» к «b»,aего величину определяем по формуле:

.

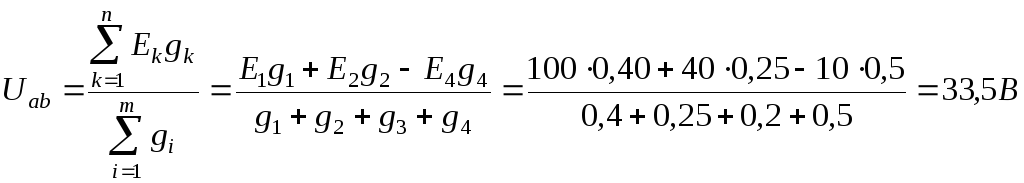ЭДС, направленные к узлу с большим потенциалом «a» (Е₁, Е₂), входят в формулу U_abсо знаком «плюс». Полученное при расчете положительное значение U_abпоказывает, что истинное направление U_abсовпадает с условно положительным.

Б.Выбираем условно положительное направление тока в ветви. При выбранном направлении U_abпотенциал узла «а» выше потенциала узла «b» Поэтому направление тока пассивной ветви выбираем совпадающим с направлением U_ab. Токи активных ветвей возьмем направленными от узла «b» к узлу «а».

В.Определяем токи в ветвях по закону Ома:

;

;

;

.

Знак «минус» тока показывает, что его истинное направление в ветви противоположно выбранному.

---

Источник ЭДС работает в режиме генератора (разряд аккумулятора), если положительное направление тока в ветви совпадает с положительным направлением ЭДС этой ветви. Если же положительные направления тока в ветви и источника ЭДС не совпадают, то ЭДС работает в режиме двигателя (заряд аккумулятора).

Если в одну из ветвей схемы с двумя узлами включен идеальный источник ЭДС, внутреннее сопротивление которого равно нулю, то узловое напряжение определяется только величиной этой ЭДС.

9.   1   2   3   4   5   6   7   8   9

---

Метод эквивалентного генератора

Метод эквивалентного генератора применяется для определения тока одной из ветвей электрической цепи в том случае, когда расчет всей схемы не требуется. В основу метода положена теорема об активном двухполюснике (теорема Гельмгольца-Тевенена). Основная идея метода заключается в том, что часть цепи, параметры которой определять нет необходимости, заменяется эквивалентным генератором с известной эдс и сопротивлением. Метод часто применяется для расчета режима электрической цепи.

Алгоритм состоит из следующих шагов:

1. 
   Выбранная для расчета ветвь удаляется из схемы, а места образовавшегося разрыва обозначаются буквами. Оставшаяся часть схемы будет представлять собой эквивалентный генератор.
   
2. 
   Рассчитывается эквивалентная эдс генератора.
   
3. 
   Определяется эквивалентное сопротивление генератора.
   
4. 
   По найденным в пунктах 2 и 3 параметрам генератора определяется ток через исключенную в пункте 1 ветвь.
   

10. 
    Цепь переменного тока и её электрические параметры (мгновенные, амплитудные действующие, средние значения электрических величин). Физический смысл сопротивлений в электрической цепи (R, X_L, X_C, Z)
    

Переменным называется ток, который с течением времени изменяет свою величину или направление. В промышленности наибольшее распространение получил синусоидальный переменный ток, то есть ток, величина которого изменяется со временем по закону синуса или косинуса. Синусоидальный переменный ток имеет целый ряд преимуществ перед постоянным током, что и объясняет его использование в промышленности и в быту.

В цепях переменного тока, кроме процессов нагрева проводов имеются дополнительные процессы, обусловленные изменяющимися магнитными и электрическими полями. Изменение этих полей оказывает влияние на величину и форму тока в цепи и может приводить к дополнительным потерям энергии. Величина и форма кривой силы тока зависят не только от параметров электрической цепи, но и от частоты и формы кривой приложенного напряжения. Поэтому анализ явлений, происходящих в цепях переменного тока, вследствие этого усложняется.

---

Изменение ЭДС и изменение тока линейной нагрузки, подключенной к такому источнику, будет происходить по синусоидальному закону. При этом переменные ЭДС, переменные напряжения и токи, можно характеризовать основными четырьмя их параметрами:

1. 
   период;
   
2. 
   частота;
   
3. 
   амплитуда;
   
4. 
   действующее значение.
   

Есть и вспомогательные параметры:

1. 
   угловая частота;
   
2. 
   фаза;
   
3. 
   мгновенное значение.
   

Любое сопротивление (металл или полупроводник) в цепи переменного токаимеет активную и реактивную составляющую. Сумма активного и реактивного сопротивления составляют полное сопротивление цепи переменного тока и вычисляется по формуле:



где, Z — полное сопротивление цепи переменного тока;

R — активное сопротивление цепи переменного тока;

Xc — емкостное реактивное сопротивление цепи переменного тока;

( С- емкость, w — угловая скорость переменного тока)

Xl — индуктивное реактивное сопротивление цепи переменного тока;

( L- индуктивность, w — угловая скорость переменного тока).

11. 
    Синусоидальный ток. Последовательное соединение активного сопротивления, индуктивности и емкости. Параллельное соединение активного сопротивления, индуктивности и емкости
    

Синусоидальным током называется периодический переменный ток, который с течением времени изменяется по гармоническому закону. Синусоидальный ток считается элементарным, то есть его невозможно разложить на другие более простые переменные токи.

Последовательное соединение активного сопротивления, индуктивности и емкости.

В схеме, состоящей из последовательно соединенных активного сопротивления, индуктивности и емкости (рис. 2.), заданы приложенное напряжение U, частота f и числовые значения параметров R, L и С. Требуется найти ток и напряжения на элементах

---

Смотрите также файлы

• Баллы 40,050,0 Оценка.docx

• День знаний 1 сентября 2022 года Самолётик будущего в день знаний предлагается заложить традицию в регионах, реализующих Всероссийский проект Навигаторы детства.docx

• Прохождении учебной практики.docx

• Rational Pharmacotherapy in Cardiology 201612(5) Рациональная Фармакотерапия в Кардиологии 201612(5).pdf

• Воспитательная работа как часть воспитательного процесса Воспитание.doc