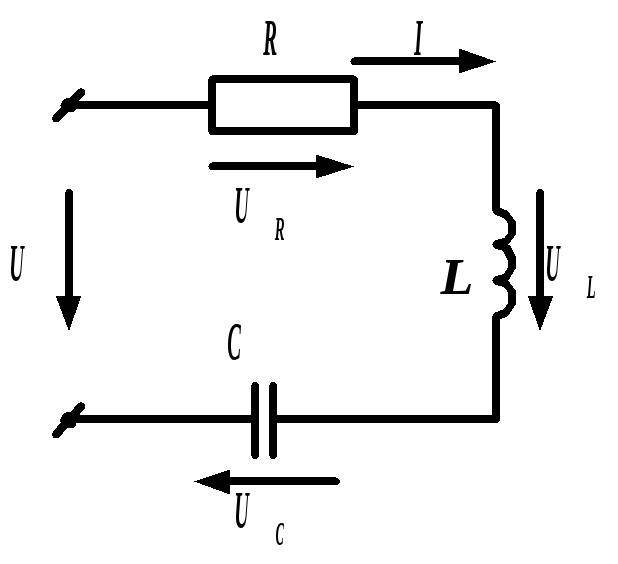
Рис. 2. Последовательная цепь переменного тока

При анализе электрических цепей синусоидального тока типична ситуация, когда метод решения незнакомой задачи неизвестен. Во многих случаях помогает следующий подход. По установленным ранее правилам строится векторная диаграмма, из анализа которой выводятся необходимые расчетные формулы. Так же поступим сейчас и мы.

В последовательной цепи общим для всех элементов является протекающий по ним ток, поэтому именно с него начинаем построение векторной диаграммы. Проводим его изображение горизонтально (рис. 2.24). Вообще, направление первого вектора при построении диаграмм произвольно. Оно диктуется соображениями удобства. Дальше мы должны показать векторы напряжений на всех элементах и в соответствии со вторым законом Кирхгофа в векторной форме   получить вектор входного напряжения. Сложение векторов можно выполнять по правилу параллелограмма, однако удобнее применять правило многоугольника, когда каждый последующий вектор пристраивается к концу предыдущего.

Параллельное соединение активного сопротивления, индуктивности и емкости

Рассмотрим схему, состоящую из параллельно соединенных активного и реактивных элементов (рис. 2.31, а).

Требуется по известным G, В_L, В_C, U рассчитать токи. Как и прежде, задачу будем решать двумя методами.

1. М е т о д в е к т о р н ы х д и а г р а м м.

Токи ветвей находятся сразу:  ,  ,  .

Для определения общего тока   необходимо построить векторную диаграмму (рис. 2.31, б). Построение начинаем с вектора напряжения, так как оно является общим для всех ветвей. Из векторной диаграммы имеем

---

или  ,

где   – полная проводимость цепи, равная

.

Разность индуктивной и емкостной проводимостей представляет собой общую реактивную проводимость цепи  .

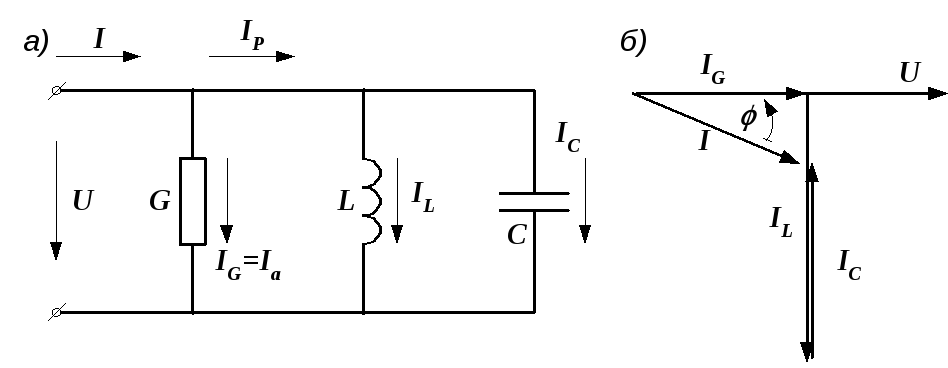Рис. 2.31. Электрическая цепь и ее векторная диаграмма

Векторы токов на диаграмме образуют треугольник токов. Его горизонтальный катет, представляющий проекцию вектора тока на вектор напряжения, называется активной составляющей тока и равен току в активном элементе цепи:   (рис. 2.32, а). Проекция вектора тока на направление, перпендикулярное напряжению, – это реактивная составляющая тока. Она равна суммарному току реактивных элементов   и определяется как разность длин векторов:  (см. рис. 2.31,б и 2.32, а).



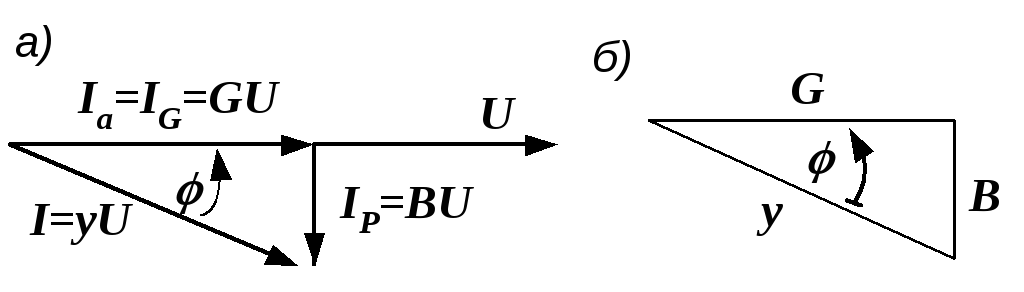
Рис. 2.32. Треугольники токов и проводимостей

Разделив все стороны треугольника токов на  , получим треугольник проводимостей (рис. 2.32, б), стороны которого связаны следующими соотношениями:

,  , 

---

,  . (2.29)

2. С и м в о л и ч е с к и й м е т о д.

Раньше были получены следующие формулы:

,  ,  .

Подставляя их в уравнение первого закона Кирхгофа, получаем:

или  ,

где   – комплексная проводимость цепи, равная

12. 
    Схемы для мгновенных, действующих и комплексных величин. Уравнения электрического состояния для мгновенных величин и в комплексной форме. Векторная диаграмма. Сопротивления: активное, реактивное, полное и комплексное. Треугольник сопротивлений
    

Активное сопротивление

, где   — импеданс,   — величина активного сопротивления,   — величина реактивного сопротивления,   — мнимая единица.

Активное сопротивление — сопротивление электрической цепи или её участка, обусловленное необратимыми превращениями электрической энергии в другие виды энергии (в тепловую).

Реактивное сопротивление

Реактивное сопротивление — электрическое сопротивление, обусловленное передачей энергии переменным током электрическому илимагнитному полю (и обратно).

Реактивное сопротивление определяет мнимую часть импеданса:

, где   — импеданс,   — величина активного сопротивления,   — величина реактивного сопротивления,   — мнимая единица.

 — элемент проявляет свойства индуктивности.

 — элемент имеет чисто активное сопротивление.

 — элемент проявляет ёмкостные свойства.

Величина реактивного сопротивления может быть выражена через величины индуктивного и ёмкостного сопротивлений:

---

Индуктивное сопротивление ( ) обусловлено возникновением ЭДС самоиндукции в элементе электрической цепи. Изменение тока и, как следствие, изменение его магнитного поля вызывает препятствующее изменению этого тока ЭДС самоиндукции. Величина индуктивного сопротивления зависит от индуктивности   элемента и частоты   протекающего тока:



Ёмкостное сопротивление ( ). Величина ёмкостного сопротивления зависит от ёмкости элемента   и также частоты протекающего тока  :



Здесь   — циклическая частота, равная  .

Прямая и обратная зависимость этих сопротивлений от частоты тока   приводит к тому, что с увеличением частоты всё бо?льшую роль начинает играть индуктивное сопротивление и всё меньшую ёмкостное.

Полное сопротивление

Полное сопротивление (z) - это векторная сумма всех сопротивлений: активного, емкостного и индуктивного.



Треугольники сопротивлений

Если стороны треугольника напряжений (155, а) разделить на ток I (.155, б), то углы треугольника от этого не изменятся, и мы получим новый треугольник, подобный первому — треугольник сопротивлений (155, в).

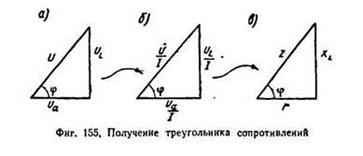В треугольнике сопротивления, показанном на рис, все стороны обозначают сопротивления, причем гипотенуза его является полным или кажущимся сопротивлением цепи.

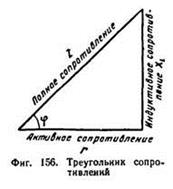Из треугольника сопротивлений видно, что полное или кажущееся сопротивление Z равно геометрической сумме активного R и индуктивного Xl сопротивлений.

Применяя теорему Пифагора к треугольнику сопротивлений, получаем:

13. 
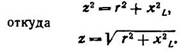    Схемы, уравнения электрического состояния для мгновенных величин в комплексной форме. Векторная диаграмма проводимости: активная, реактивная, полная и комплексная. Треугольник проводимостей. Эквивалентное комплексное сопротивление цепи
    

---

Треугольники проводимостей и токов.

Представим комплексную проводимость в алгебраической форме



Действительную часть комплексной проводимости С называют активной проводимостью, а мнимую В — реактивной. На рис. 2.10.2, а сделаны построения, соответствующие комплексному выражению (2.10.5).



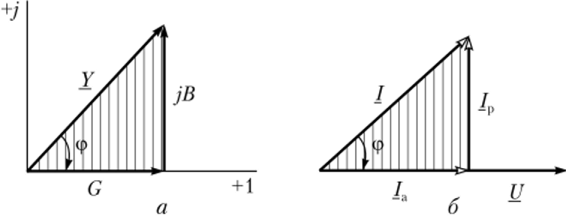
Рис. 2.10.2. Треугольники проводимостей (а) и токов (б)

Заштрихованный прямоугольный треугольник на рис. 2.10.2, а называют треугольником проводимостей. Из треугольника очевидны соотношения



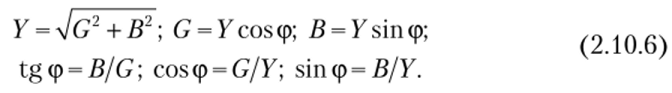
Выразим активную и реактивную составляющие проводимости ветви через ее активное и реактивное сопротивления. Рассмотрим, например, проводимость ветви с элементами /?, и]Хр



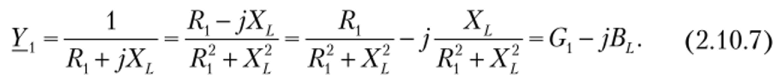
При получении соотношения (2.10.7) числитель и знаменатель умножены на сопряженный комплекс 

Следует обратить внимание на то, что мнимая часть комплексной проводимости ветви с индуктивным элементом отрицательная. Если бы подобным образом было получено соотношение для второй ветви, содержащей емкостный элемент, то формулы имели бы тот же вид, но мнимая часть была бы положительной.

Итак, 

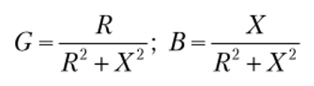
или



Построение треугольника тока очевидно из рис. 2.10.2, б. На векторной диаграмме рис. 2.10.2, б вектор тока спроецирован на направление вектора напряжения. Полученный при этом треугольник называют треугольником тока. Катеты прямоугольного треугольника тока называют активной и реактивной составляющими: активная составляющая тока /а параллельна напряжению, а реактивная /р — ортогональна. Из треугольника тока можно получить следующие выражения активной и реактивной составляющих тока:

---

Смотрите также файлы

• Баллы 40,050,0 Оценка.docx

• День знаний 1 сентября 2022 года Самолётик будущего в день знаний предлагается заложить традицию в регионах, реализующих Всероссийский проект Навигаторы детства.docx

• Прохождении учебной практики.docx

• Rational Pharmacotherapy in Cardiology 201612(5) Рациональная Фармакотерапия в Кардиологии 201612(5).pdf

• Воспитательная работа как часть воспитательного процесса Воспитание.doc