Файл: Цель работы ознакомиться и понять смысл уравнения Бернулли, уметь применять его для решения практических задач гидродинамики. Схема лабораторной установки.docx

Второй вариант – вращение сосуда с жидкостью с постоянной угловой скоростью ω вокруг центральной оси. Несмотря на то, что вся масса жидкости вращается вместе с сосудом, частицы жидкости друг относительно друга не перемещаются, следовательно, весь объём жидкости, как и в первом случае, представляет собой как бы твёрдое тело. Давление в каждой точке жидкости не меняется во времени и зависит только от координат. По этим причинам жидкость подпадает под определение покоящейся.

Третий вариант аналогичен второму, только вращение осуществляется вокруг произвольно расположенной вертикальной оси. Во втором и третьем случае свободная поверхность жидкости принимает новую форму, соответствующую новому равновесному положению жидкости.

В четвёртом варианте сосуд с жидкостью движется прямолинейно и равноускоренно. Такой случай проявляется, например, в процессе разгона или остановки автоцистерны с жидкостью. В этом случае жидкость занимает новое равновесное положение, свободная поверхность приобретает наклонное положение, которое сохраняется до изменения ускорения. Частицы жидкости друг относительно друга находятся в покое, и давление зависит только от координат.

Во всех перечисленных случаях на жидкость действуют, силы веса, силы инерции, силы давления.

4. 
   Уравнение Д. Бернулли представляет собой математическое выражение закона сохранения энергии потока жидкости и является основным расчётным уравнением современной гидравлики и гидромеханики, на базе которого решаются многие практические задачи. Уравнение Д. Бернулли для двух живых сечений потока вязкой несжимаемой жидкости в случае установившегося его движения имеет следующий вид:
   

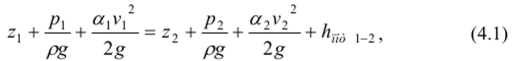
где z - геометрический напор или высота положения - расстояние от произвольно выбранной горизонтальной плоскости сравнения (отсчёта) до центра тяжести сечения (в энергетическом смысле - это мера удельной, т.е. отнесённой к единице веса жидкости потенциальной энергии положения); р - давление в центре тяжести сечения; р/pg - пьезометрический напор - вертикальное рас



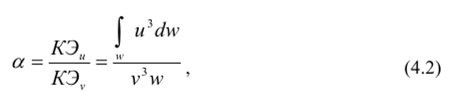
стояние между центром тяжести сечения и уровнем жидкости в пьезометре (в энергетическом смысле - мера удельной потенциальной энергии давления в рассматриваемом живом сечении потока); v - средняя скорость потока в сечении; 

---

а - коэффициент Кориолиса (корректив кинетической энергии), представляющий собой отношение действительной кинетической энергии потока к условной кинетической энергии, вычисленной по средней скорости v. Значение коэффициента Кориолиса а изменяется от 1 до 2. Для ламинарного режима движения жидкости а = 2...5, при турбулентном режиме а близок к 1,0. В каждом конкретном случае коэффициент « может быть определён экспериментально по формуле

5. 
   Различают следующие виды давления: барометриче­ское, абсолютное, манометрическое и вакуумметрическое.
   

Барометрическое давление

Барометрическое (атмосферное) давление р_бзависит от высоты места над уровнем моря и от состояния погоды, За нормальное барометрическое давление принимают давление, равное 760 мм ртутного столба, что соот­ветствует 101325 Н/м². На уровне моря барометрическое давление наблюдалось в пределах от 90 000 Н/м²до 110000 Н/м². С высотой барометрическое давление убывает. Наоборот, в глубоких шахтах барометрическое давление значительно больше, чем на уровне моря.

Абсолютное и манометрическое давление

Давление р_авычисленное по уравнению (6), называется абсолютным. Рассмотрим наиболее распространенный в практике случай (рис.7), когда к свободной поверхности приложено баро­метрическое давление р_б, т. е. р₀ = р₆. 

Вопросы по гидродинамике:

1. 
   Кинематика Кинематика жидкости– раздел гидромеханики, в котором изучают виды и характеристики движения жидкости, но не рассматривают силы, под действием которых это движение происходит.
   
2. 
   Установившимся называют такое движение жидкости, при котором скорость потока и гидродинамическое давление в любой точке не изменяются с течением времени, а зависят только от положения рассматриваемой точки в потоке жидкости, т. е. являются функциями ее координат. Примерами установившегося движения могут быть истечение жидкости из отверстия резервуара при постоянном напоре, поток воды в канале при неизменном его поперечном сечении и постоянной глубине. Неустановившимся называют такое движение жидкости, при котором скорость потока и давление в каждой данной точке изменяются во времени. Примером неустановившегося движения служит истечение жидкости из отверстия резервуара при переменном напоре. Равномерным называют такое установившееся движение жидкости, при котором живые сечения и средняя скорость потока не меняются по его длине. Равномерным можно считать движение жидкости в трубе или канале неизменного сечения и постоянной глубины. Неравномерным называют такое установившееся движение жидкости, при котором живые сечения и средние скорости потока изменяются по его длине. Неравномерным считают движение жидкости в конической трубе и в естественном русле. Напорным называют такое движение жидкости, при котором заполняется все поперечное сечение трубопровода под давлением выше атмосферного; движение жидкости осуществляется за счет сил давления, т. е. за счет напора, создаваемого затратой дополнительной энергии. Безнапорным называют такое движение жидкости, при котором у потока имеется свободная поверхность, находящаяся под атмосферным давлением.
   

---

3. 
   Уравнения неразрывности потока являются приложением закона сохранения масс для гидравлики. С другой стороны, обывательское выражение «сколько в трубу поступило жидкости, столько из нее и выльется» справедливо только если рассматривать начальный и конечный моменты работы гид-равлической системы или при условии постоянства давлений в трубопроводах (такое предположение справедливо только для статического расчета системы). Если в системе происходят переходные процессы, которые неизбежно связаны с изменением давления, подача поступающей в трубопровод жидкости отличается от расхода на выходе из трубопровода на величину расхода на деформацию жидкости и стенок трубопровода. Тогда уравнение неразрывности потока в общем виде:
   

, (1.23)

4. 
   Рассмотрим одно из основных уравнений гидродинамики – уравнение Бернулли, которое представляет собой математическое выражение закона сохранения энергии. Это уравнение широко применяется при проведении инженерных расчетов. для случая слабодеформированного потока это уравнение обычно дополняется уравнением неразрывности (4.4)
   

Для получения уравнения Бернулли рассмотрим энергетические преобразования, происходящие в элементарной струйке (рис. 5.2).



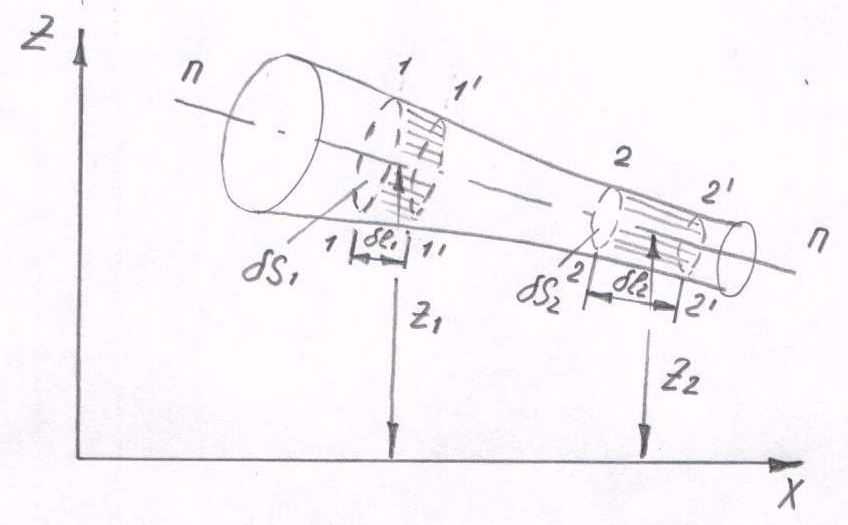
Рис. 5.2. К выводу уравнения Бернулли

В струйке, определяемой осью n-n проведем сечения 1 и 2. За время t сечение 1 переместится на l₁ в положение 1', а сечение 2 – на l₂ в положение 2'. При этом по условию неразрывности (4.3)

;  ;

–элементарный объем жидкости.

Объем 1-2 за время t в результате движения жидкости перемещается в положение 1-2'. Так как движение потока считаем установившимся, то в его части, выделенной сечениями 1' и 2, изменения параметров не происходит. Поэтому все изменения, в том числе и энергии, произошедшие в результате перемещения объема 1-2 в положение 1'-2' происходят вследствие перемещения объема W из положения 1-1' в положение 2-2'.

---

Из-за малых поперечных размеров элементарной струйки можно считать, что все частицы объема 1-1' движутся со скоростью V₁ , а объема 2-2' - со скоростью V₂.

5. 
   Геометрический смысл уравнения Бернулли
   

Все члены в уравнении Бернулли представляют собой геометрические высоты и имеют размерность длины.

Так как сумма трех членов  , z и  для идеальной жидкости постоянна вдоль оси струйки, то уровни жидкости в трубках Пито, установленных в различных сечениях будут всегда лежать в одной горизонтальной плоскости, называемой напорной плоскостью. В этом состоит геометрический смысл уравнения Бернулли для идеальной жидкости.

Сумма трех высот называется полным напором и обозначается Н_g, т.е. полный напор представляет собой сумму пьезометрического  и скоростного напоров:

С энергетической точки зрения уравнение Бернулли выражает закон сохранения энергии. Полный напор  - это полная удельная механическая энергия жидкости в рассматриваемом сечении. Сумма трех членов есть сумма трех удельных энергий: удельной потенциальной энергии давления  , удельной потенциальной энергии положенияz, удельной кинетической энергии  . Для идеальной жидкости сумма трех удельных энергий (полный напор) по длине струйки есть величина постоянная.

Для потока реальной жидкости уравнение Бернулли имеет вид

---

 где v₁и v₂ - средние скорости движения жидкости в рассматриваемых сечениях;  ₁и  ₂ - коэффициенты кинетической энергии, величина которых зависит от степени неравномерности распределения скоростей по живому сечению потока.

6. 
   В реальных потоках жидкости присутствуют силы вязкого трения. В результате слои жидкости трутся друг об друга в процессе движения. На это трение затрачивается часть энергии потока. По этой причине в процессе движения неизбежны потери энергии. Эта энергия, как и при любом трении, преобразуется в тепловую энергию. Из-за этих потерь энергия потока жидкости по длине потока, и в его направлении постоянно уменьшается. Т.е. напор потока H_потока в направлении движения потока становится меньше. Если рассмотреть два соседних сечения 1-1 и 2-2, то потери гидродинамического напора Δh составят:
   

,

где H_1-1- напор в первом сечении потока жидкости,

H_2-2 - напор во втором сечении потока,

∆h - потерянный напор - энергия, потерянная каждой единицей веса движущейся жидкости на преодоление сопротивлений на пути потока от сечения 1-1 до сечения 2-2.

С учётом потерь энергии уравнение Бернулли для потока реальной жидкости будет выглядеть



Индексами 1 и 2 обозначены характеристики потока в сечениях 1-1 и 2-2.

Если учесть, что характеристики потока V и α зависят от геометрии потока, которая для напорных потоков определяется геометрией трубопровода, понятно, что потери энергии (напора) в разных трубопроводах будут изменяться неодинаково. Показателем изменения напора потока является гидравлический уклон I, который характеризует потери напора на единице длины потока. Физический смысл гидравлического уклона – интенсивность рассеяния энергии по длине потока. Другими словами, величина I показывает, как быстро трубопровод поглощает энергию потока, протекающего в нём

---