Файл: Цель работы ознакомиться и понять смысл уравнения Бернулли, уметь применять его для решения практических задач гидродинамики. Схема лабораторной установки.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 1743
Скачиваний: 99
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Практическое задание для допуска к виртуальным лабораторным работам
(экспериментальное изучение и практическая реализация)
«Определение гидростатического давления жидкости»
Лабораторная работа 2«Сила давления жидкости на плоскую поверхность»
Лабораторная работа 3«Определение динамических коэффициентов для оценки расхода жидкости»
Лабораторная работа 4«Построение напорной и пьезометрической линий для трубопровода сопротивления»
Лабораторная работа 4«Построение напорной и пьезометрической линий для трубопровода сопротивления»
Тема. Гидродинамика трубопроводов: интерпретация параметров уравнения Д. Бернулли в трубопроводе с местными сопротивлениями.
Цель работы:
1.Определение опытным путем потерь напора на преодоление сопротивления по длине трубопровода и на участках с местными сопротивлениями.
2.Расчет коэффициентов местных потерь и коэффициентов Дарси.
3.Построение напорной и пьезометрической линий.
Проведение работы
Схематическое изображение трубопровода сопротивления показано на рис. 4.1.
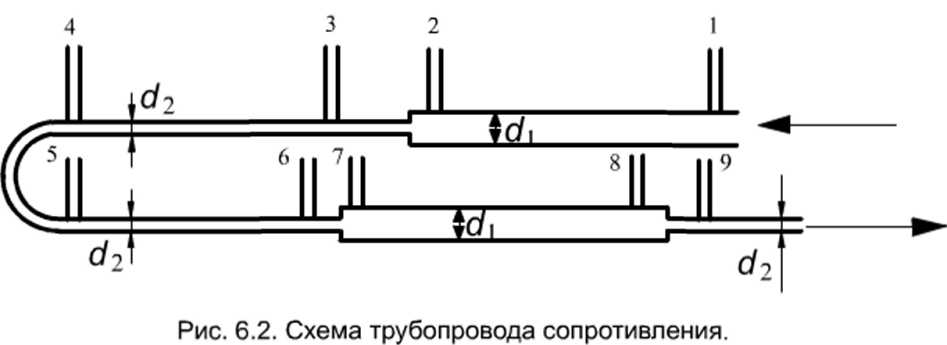
Рисунок 4.1 – Схема трубопровода сопротивления
Методические рекомендации
Полная удельная энергия жидкости в рассматриваемом сечении(напор) для установившегося потока определяется суммой удельных кинетической и потенциальной энергий:
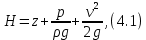
где z– удельная энергия положения (может быть представлена расстоянием от плоскости сравнения до оси потока) (геометрический напор), м;
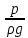 – удельная энергия давления (высота поднятия жидкости в пьезометре (пьезометрический напор) м;
– удельная энергия давления (высота поднятия жидкости в пьезометре (пьезометрический напор) м;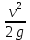 – удельная кинетическая энергия (скоростной напор), м.
– удельная кинетическая энергия (скоростной напор), м.Известно, что при движении вязкой жидкости ее напор уменьшается вниз по течению, так как часть потенциальной энергии расходуется на преодоление сопротивлений. Если удельная потенциальная энергия, израсходованная жидкостью на преодоление сопротивлений между первым и вторым сечениями, равна hтр, то уравнение Бернулли, связывающее удельные полные энергии в этих двух сечениях, будет иметь вид (4.2).Полная удельная энергия жидкости в рассматриваемом сечении (напор) для установившегося потока определяется суммой удельных кинетической и потенциальной энергий:
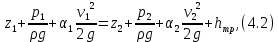
где 1 и 2 – индексы параметров, соответственно, начала и конца потока; hтр – напор, израсходованный на преодоление местных сопротивлений и сопротивлений по длине (
hтр=hм+hдл.).
Местные потери энергии и потери энергии по длине зависят от величины кинетической энергии:
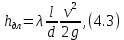
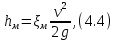
где
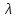 – коэффициент сопротивления трения по длине, или коэффициент Дарси;
– коэффициент сопротивления трения по длине, или коэффициент Дарси; – длина потока, м;d– диаметр трубопровода, м;
– длина потока, м;d– диаметр трубопровода, м;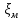 – коэффициент местных потерь.
– коэффициент местных потерь.Удельные кинетическая и потенциальная энергии потока связаны между собой. В частности, если кинетическая энергия жидкости уменьшается, что проявляется в уменьшении скорости движения, то потенциальная энергия увеличивается, что приводит к соответствующему увеличению давления.
Построение напорной и пьезометрической линий для трубопровода сопротивления. Определение коэффициентов местных сопротивлений и коэффициентов трения по длине
Изменение удельной энергии жидкости можно изобразить графически, откладывая в масштабе для наблюдаемых сечений величины удельной энергии положения, энергии давления и кинетической энергии.
Линия, соединяющая точки, соответствующие значениям суммы всех видов энергии, называется линией полной удельной энергии, или напорной линией. Линия, соединяющая точки, соответствующие значению потенциальной энергии, называется линией удельной потенциальной энергии, или пьезометрической линией (рис. 4.1).
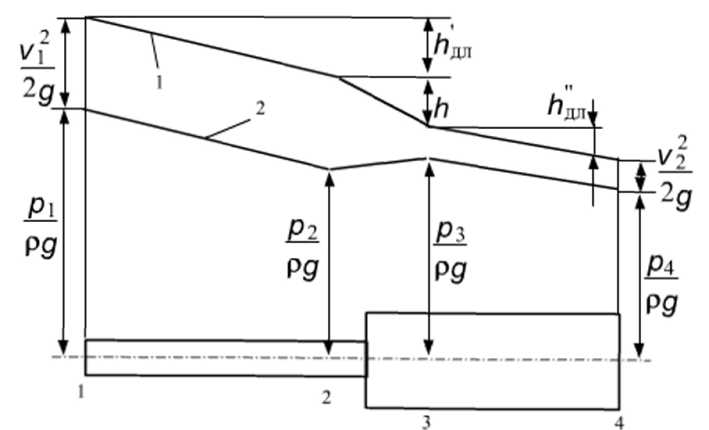
Рисунок 4.1 – Пример построения напорной и пьезометрической линий
Определение пьезометрической высоты h = p/
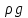 производится с помощью пьезометра; она равна высоте поднятия столба жидкости в пьезометре. Для рассматриваемого трубопровода плоскость сравнения совпадает с осью горизонтальной части трубопровода, поэтому величина
производится с помощью пьезометра; она равна высоте поднятия столба жидкости в пьезометре. Для рассматриваемого трубопровода плоскость сравнения совпадает с осью горизонтальной части трубопровода, поэтому величина
z во всех сечениях будет равна 0.
Определение средней скорости жидкости производится по формуле
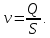 (4.5)
(4.5)Расход определяется с помощью расходомерного прибора – ротаметра.
Рассматривая рис. 4.1, можно увидеть, как изменяется полная удельная энергия потока, а следовательно, скорость и давление в зависимости от изменения сечения трубопровода. В частности, при внезапном расширении давление в потоке увеличивается, что объясняется уменьшением скорости движения.
Удельная энергия, израсходованная на преодоление сопротивления в любом местном сопротивлении, может быть определена как разность полной удельной энергии до и после сопротивления, например, для участка 2–3:
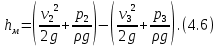
Удельная энергия, израсходованная на преодоление сопротивления трения по длине, может быть определена по разности показаний пьезометров, так как кинетическая энергия на протяжении трубопровода считается постоянной.
Так, для сечений 1 и 2
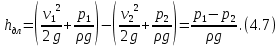
Таким образом, для определения
 и
и  по уравнениям (4.3) и (4.4) необходимо знать величины hдли hм для соответствующих участков. Эти величины находим из уравнений (4.6) и (4.7), используя результаты измерений. Следует отметить, что при определенииhм по уравнению (4.4) кинетическая энергия рассчитывается по скорости, которой обладает поток за местным сопротивлением, т.е. при определении hм на участке 2–3 в формулу (4.4) подставляется скорость на участке 3.
по уравнениям (4.3) и (4.4) необходимо знать величины hдли hм для соответствующих участков. Эти величины находим из уравнений (4.6) и (4.7), используя результаты измерений. Следует отметить, что при определенииhм по уравнению (4.4) кинетическая энергия рассчитывается по скорости, которой обладает поток за местным сопротивлением, т.е. при определении hм на участке 2–3 в формулу (4.4) подставляется скорость на участке 3.Проведение работы
Вода из напорного бака поступает в трубопровод сопротивления, протекая через который, сливается в канализацию.
Трубопровод сопротивления выполнен из труб диаметрами d1= 2610–3м и d2 = 1610–3 ми состоит из 8 участков (рис. 4.1).
Измерение давлений производится пьезометрами в указанных на схеме сечениях. Расход жидкости через трубопровод измеряют с помощью ротаметра и регулируют вентилем. Опытные данные заносят в табл. 4.1. Результаты расчетов скоростей, потерь всех видов и коэффициентов – в табл. 4.2.
Таблица 4.1
| Параметры | Номер сечения | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| Показания пьезометра h =  ,м ,м | 1,479 | 1,477 | 1,473 | 1,469 | 1,455 | 1,448 | 1,457 | 1,449 | 1,398 |
| Q, м3/с*10-5 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 |
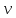 , м/с , м/с | 0,132 | 0,132 | 0,348 | 0,348 | 0,348 | 0,348 | 0,132 | 0,132 | 0,348 |
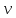 2/2g 2/2g | 0,0009 | 0,0009 | 0,0062 | 0,0062 | 0,0062 | 0,0062 | 0,0009 | 0,0009 | 0,0062 |
Таблица 4.2
| Величина | Участок | |||||||
| 1–2 | 2–3 | 3–4 | 4–5 | 5–6 | 6–7 | 7–8 | 8–9 | |
| L, м | 1,07 | – | 0,64 | – | 0,44 | – | 1,17 | – |
| d10–3,м | 26 | 26–16 | 16 | 16 | 16 | 16–26 | 26 | 26–16 |
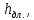 м м | 0,002 | | 0,004 | | 0,007 | | 0,008 | |
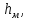 м м | | 0,004 | | 0,014 | | -0,009 | | 0,051 |
 | 0,0548 | | 0,0263 | | 0,0669 | | 0,2005 | |
 | | 4,51 | | 2,26 | | -1,46 | | 57,51 |
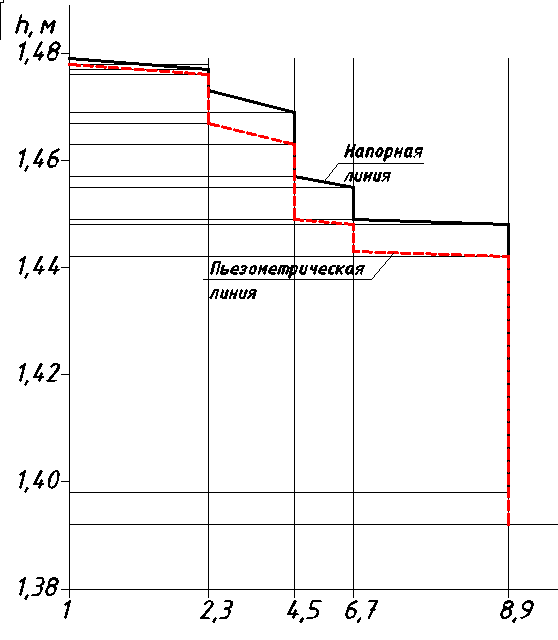
Рисунок 4.2 – Напорная и пьезометрическая линия
Общие выводы по выполненной работе:
В выполненной лабораторной работе мы ознакомились с общими законами гидродинамики трубопроводов: интерпретация параметров уравнения Д. Бернулли в трубопроводе с местными сопротивлениями.
В выполненной лабораторной работе был поставлен опыт в ходе которого была найдены пьезометрические высоты в характерных сечениях трубопровода. По результатам опыта определили значение коэффициента сопротивления трения по длине для каждого участка и коэффициент местных потерь для сечений с изменением диаметра.
Контрольные вопросы
Вопросы по гидростатике:
-
Гидростатическое давление и его свойства. -
Силы, действующие в жидкости. -
Система дифференциальных уравнений Эйлера. Основное дифференциальное уравнение покоящейся жидкости. -
Основное уравнение гидростатики в поле земного тяготения. -
Виды давления. Приборы для измерения давления жидкости. Сила давления жидкости на плоские и криволинейные поверхности.
Вопросы по гидродинамике:
-
Основные понятия кинематики жидкости. Основные элементы потока движущейся жидкости. -
Виды движения жидкости. -
Уравнение неразрывности потока. -
Основное уравнение баланса гидравлических параметров (уравнение Д. Бернулли. Написать уравнение Бернулли для установившегося потока несжимаемой жидкости и пояснить его. Чем его можно подтвердить в данной работе? -
Геометрическая и энергетическая интерпретация уравнения Д. Бернулли. Что понимается под удельной энергией и какова ее размерность? -
Формы представления уравнения Д. Бернулли для потока реальной жидкости. Где можно применить уравнение Бернулли? -
Назначение трубки Пито. Что с ее помощью можно определить? -
Как определяются уклоны? Какие из них могут принимать положительные и отрицательные значения? -
Чем объясняется резкое изменение напорной линии на графике и какой практический вывод можно сделать из этого факта? -
Уравнение Бернулли для элементарной струйки невязкой сжимаемой жидкости.
Вопросы по гидростатике:
-
Гидростатическое давление – это давление, производимое на жидкость силой тяжести. -
Силы, действующие в жидкости, подразделяются на объемные (массовые) и поверхностные. -
Дифференциальные уравнения равновесия покоящейся жидкости иначе называют дифференциальными уравнениями Эйлера. Они получены для общего случая относительного покоя жидкости. Возможны следующие варианты относительного покоя. Первый вариант соответствует абсолютному покою или равномерному движению сосуда с жидкостью. Такой вариант рассматривался при выводе основного уравнения гидростатики.