Файл: Цель работы ознакомиться и понять смысл уравнения Бернулли, уметь применять его для решения практических задач гидродинамики. Схема лабораторной установки.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 1751
Скачиваний: 99
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Практическое задание для допуска к виртуальным лабораторным работам
(экспериментальное изучение и практическая реализация)
«Определение гидростатического давления жидкости»
Лабораторная работа 2«Сила давления жидкости на плоскую поверхность»
Лабораторная работа 3«Определение динамических коэффициентов для оценки расхода жидкости»
Лабораторная работа 4«Построение напорной и пьезометрической линий для трубопровода сопротивления»
, сжимается так, что площадь сечения струи Sстановится меньше площади отверстия диафрагмы Scr. В дальнейшем поток занимает всё сечение трубопровода.
Применяя уравнение Бернулли к сечениям 1 и 2, получим:
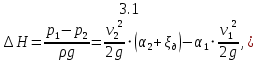 )
)
где p1 и р2– давление, соответственно, в сечениях 1 и 2;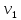 и
и 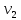 – средняя скорость движения в сечениях 1 и 2;
– средняя скорость движения в сечениях 1 и 2;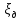 – коэффициент потерь диафрагмы;
– коэффициент потерь диафрагмы;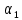 и
и 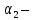 коэффициент кинетической энергии в сечениях 1 и 2.
коэффициент кинетической энергии в сечениях 1 и 2.
Коэффициент кинетической энергии учитывает неравномерность распределения истинных скоростей в этих сечениях и представляет собой отношение действительной кинетической энергии потока к кинетической энергии, вычисленной по средней скорости.
Имея в виду, что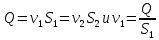 ,а также заменяя скорости
,а также заменяя скорости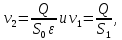 получим:
получим:
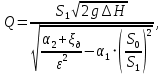
где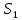 и
и 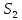 – соответственно, площади живых сечений 1 и 2, м2;
– соответственно, площади живых сечений 1 и 2, м2;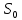 – площадь отверстия диафрагмы, м2;
– площадь отверстия диафрагмы, м2;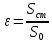 – коэффициент сжатия.
– коэффициент сжатия.
Обозначая
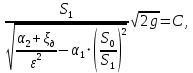
где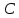 – коэффициент дроссельного прибора, получим
– коэффициент дроссельного прибора, получим
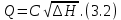
Таким образом, для определения расхода в промышленных условиях с помощью диафрагмы нужно знать значение коэффициента дроссельного прибора и показание жидкостного дифференциального манометра, выраженное высотой водяного столба.
Опыт 2. Водомер Вентури
Водомер Вентури (рис. 3.2), или, как его еще называют, двухконусный водомер, представляет собой сужающийся прибор, но
сужение потока в нем осуществляется плавно, без создания застойных вихревых зон, как это имеет место в диафрагме.
Отсутствие застойных зон позволяет резко снизить гидравлические сопротивления при прохождении жидкости через данный прибор, что дает возможность использовать водомер для измерения очень больших расходов жидкости.
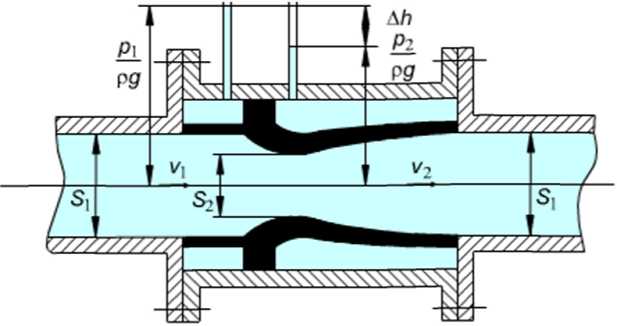
Рисунок3.2 – Схема устройства водомера Вентури
Применяя уравнение Бернулли для идеальной жидкости относительно сечений 1 и 2, получим:
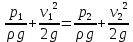 .
.
Разность давлений, фиксируемая дифференциальным манометром, представляет собой разность кинетических энергий в этих сечениях:
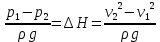 .
.
Выражая скорость по уравнению сплошности через
по уравнению сплошности через  , получим:
, получим:
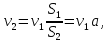
где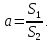
Определим скорость в сечении 1–1:
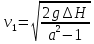 .
.
По скорости находим теоретический расход потока:
находим теоретический расход потока:
Qt= S1. (3.3)
S1. (3.3)
При движении вязкой жидкости расход будет меньше и может быть определен по формуле действительного расхода:
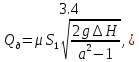 )
)
где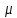 – коэффициент расхода водомера – величина, показывающая, во сколько раз действительный расход меньше теоретического.
– коэффициент расхода водомера – величина, показывающая, во сколько раз действительный расход меньше теоретического.
В данной работе требуется определить значение коэффициента расхода:
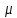 =
=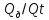 . (3.5)
. (3.5)
Для этого необходимо определить с помощью объёмного счетчика расхода действительный расход:
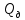 =
= 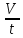
и теоретический расход по уравнению (3.3).
Отношение площадей:
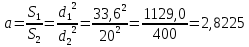
Проведение работы
Регулирующим вентилем устанавливают расход жидкости через приборы. Записывают показания соответствующих данному прибору пьезометров и определяют расход жидкости. Данные заносят в табл. 3.1.
Далее изменяют расход жидкости с помощью того же вентиля и повторяют все измерения. Количество опытов должно быть не менее 8–10. Все расчетные данные заносят в табл. 3.2.
Тарировочные графики строят в масштабе на миллиметровой бумаге. Такие графики значительно упрощают контроль за расходом жидкости при использовании диафрагмы и водомера в технологическом процессе, так как исключают необходимость проведения расчетов.
Таблица 3.1
Таблица 3.2
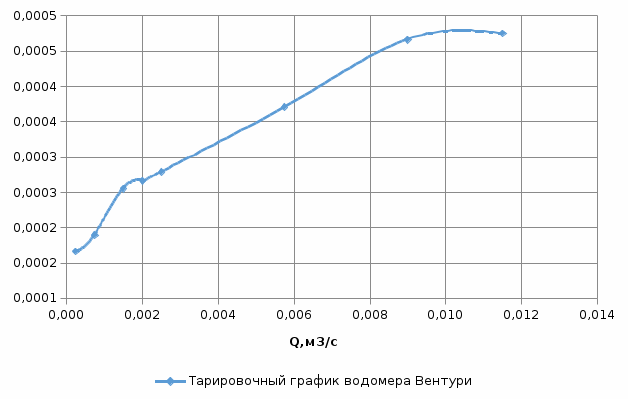
Рисунок 3.3 – Тарировочный график водомера Вентури, т.е. зависимость Qв= f( Нв)
Нв)
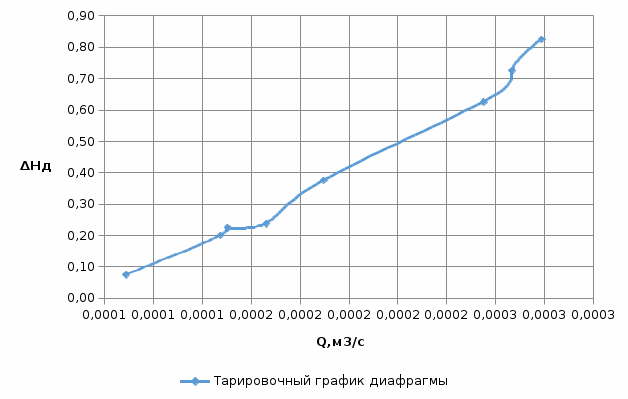
Рисунок 3.4 – Тарировочный график диафрагмы, т.е. зависимость Qд = f( Нд)
Нд)
Общие выводы по выполненной работе:
В выполненной лабораторной работе мы ознакомились с общими законами гидродинамики трубопроводов: определение гидродинамических параметров потока движущейся жидкости при прохождении через измерительные приборы, представляющие местные сопротивления
В выполненной лабораторной работе был поставлен опыт в ходе которого была найдены перепады давления на диафрагме и водомере Вентури. По результатам опыта определили значение коэффициента расхода для водомера Вентури. По результатам расчетов построили тарировочные графики устройств.
Применяя уравнение Бернулли к сечениям 1 и 2, получим:
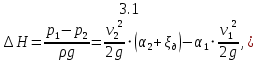 )
)где p1 и р2– давление, соответственно, в сечениях 1 и 2;
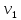 и
и 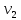 – средняя скорость движения в сечениях 1 и 2;
– средняя скорость движения в сечениях 1 и 2;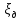 – коэффициент потерь диафрагмы;
– коэффициент потерь диафрагмы;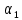 и
и 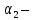 коэффициент кинетической энергии в сечениях 1 и 2.
коэффициент кинетической энергии в сечениях 1 и 2. Коэффициент кинетической энергии учитывает неравномерность распределения истинных скоростей в этих сечениях и представляет собой отношение действительной кинетической энергии потока к кинетической энергии, вычисленной по средней скорости.
Имея в виду, что
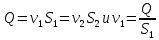 ,а также заменяя скорости
,а также заменяя скорости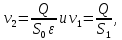 получим:
получим: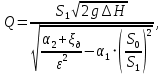
где
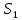 и
и 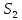 – соответственно, площади живых сечений 1 и 2, м2;
– соответственно, площади живых сечений 1 и 2, м2;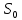 – площадь отверстия диафрагмы, м2;
– площадь отверстия диафрагмы, м2;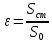 – коэффициент сжатия.
– коэффициент сжатия.Обозначая
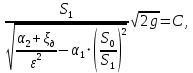
где
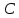 – коэффициент дроссельного прибора, получим
– коэффициент дроссельного прибора, получим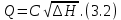
Таким образом, для определения расхода в промышленных условиях с помощью диафрагмы нужно знать значение коэффициента дроссельного прибора и показание жидкостного дифференциального манометра, выраженное высотой водяного столба.
Опыт 2. Водомер Вентури
Водомер Вентури (рис. 3.2), или, как его еще называют, двухконусный водомер, представляет собой сужающийся прибор, но
сужение потока в нем осуществляется плавно, без создания застойных вихревых зон, как это имеет место в диафрагме.
Отсутствие застойных зон позволяет резко снизить гидравлические сопротивления при прохождении жидкости через данный прибор, что дает возможность использовать водомер для измерения очень больших расходов жидкости.

Рисунок3.2 – Схема устройства водомера Вентури
Применяя уравнение Бернулли для идеальной жидкости относительно сечений 1 и 2, получим:
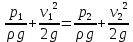 .
.Разность давлений, фиксируемая дифференциальным манометром, представляет собой разность кинетических энергий в этих сечениях:
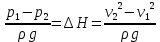 .
.Выражая скорость
 по уравнению сплошности через
по уравнению сплошности через  , получим:
, получим: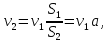
где
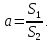
Определим скорость в сечении 1–1:
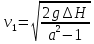 .
.По скорости
 находим теоретический расход потока:
находим теоретический расход потока:Qt=
 S1. (3.3)
S1. (3.3)При движении вязкой жидкости расход будет меньше и может быть определен по формуле действительного расхода:
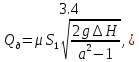 )
)где
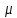 – коэффициент расхода водомера – величина, показывающая, во сколько раз действительный расход меньше теоретического.
– коэффициент расхода водомера – величина, показывающая, во сколько раз действительный расход меньше теоретического.В данной работе требуется определить значение коэффициента расхода:
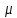 =
=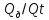 . (3.5)
. (3.5)Для этого необходимо определить с помощью объёмного счетчика расхода действительный расход:
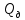 =
= 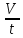
и теоретический расход по уравнению (3.3).
Отношение площадей:
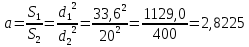
Проведение работы
Регулирующим вентилем устанавливают расход жидкости через приборы. Записывают показания соответствующих данному прибору пьезометров и определяют расход жидкости. Данные заносят в табл. 3.1.
Далее изменяют расход жидкости с помощью того же вентиля и повторяют все измерения. Количество опытов должно быть не менее 8–10. Все расчетные данные заносят в табл. 3.2.
Тарировочные графики строят в масштабе на миллиметровой бумаге. Такие графики значительно упрощают контроль за расходом жидкости при использовании диафрагмы и водомера в технологическом процессе, так как исключают необходимость проведения расчетов.
Таблица 3.1
| № опыта | Сетепень открытия вентиля | V, м3 | t, сек. | Диафрагма | Водомер Вентури | ||
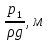 | 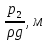 | 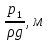 | 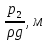 | ||||
| 1 | 1 | 0,0890 | 187,3 | 1,025 | 0,000 | 0,0133 | 0,0018 |
| 2 | 0,9 | 0,0339 | 72,7 | 1,075 | 0,000 | 0,0135 | 0,0045 |
| 3 | 0,8 | 0,0215 | 58,0 | 1,150 | 0,000 | 0,0138 | 0,0080 |
| 4 | 0,7 | 0,0160 | 57,4 | 1,275 | 0,450 | 0,0145 | 0,0120 |
| 5 | 0,65 | 0,0156 | 58,5 | 1,300 | 0,575 | 0,0146 | 0,0126 |
| 6 | 0,6 | 0,0152 | 59,6 | 1,325 | 0,700 | 0,0148 | 0,0133 |
| 7 | 0,5 | 0,0081 | 42,7 | 1,375 | 1,000 | 0,0150 | 0,0143 |
| 8 | 0,4 | 0,0067 | 40,3 | 1,438 | 1,200 | 0,0150 | 0,0148 |
| 9 | 0,3 | 0,0080 | 53,2 | 1,450 | 1,225 | 0,0153 | 0,0150 |
| 10 | 0,25 | 0,0082 | 55,6 | 1,475 | 1,275 | 0,0155 | 0,0153 |
| 11 | 0,2 | 0,0070 | 64,3 | 1,475 | 1,400 | 0,0153 | 0,0150 |
Таблица 3.2
| №опыта | Диафрагма | | Водомер Вентури | |||||
 Нд,м Нд,м | Qд, м3/с | С, м2/с |  Нв, м Нв, м | Qд,м3/с | Vt,м/с | 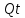 , м3/с , м3/с |  | |
| 1 | 1,025 | 0,000475 | 0,0004693 | 0,0115 | 0,000475 | 0,180 | 0,000203 | 0,427 |
| 2 | 1,075 | 0,000466 | 0,0004497 | 0,0090 | 0,000466 | 0,159 | 0,000180 | 0,385 |
| 3 | 1,150 | 0,000371 | 0,0003457 | 0,0058 | 0,000371 | 0,127 | 0,000144 | 0,387 |
| 4 | 0,825 | 0,000279 | 0,0003069 | 0,0025 | 0,000279 | 0,084 | 0,000095 | 0,340 |
| 5 | 0,725 | 0,000267 | 0,0003132 | 0,0020 | 0,000267 | 0,075 | 0,000085 | 0,318 |
| 6 | 0,625 | 0,000255 | 0,0003226 | 0,0015 | 0,000255 | 0,065 | 0,000073 | 0,288 |
| 7 | 0,375 | 0,000190 | 0,0003098 | 0,0007 | 0,000190 | 0,046 | 0,000052 | 0,273 |
| 8 | 0,238 | 0,000166 | 0,0003411 | 0,0002 | 0,000166 | 0,027 | 0,000030 | 0,180 |
| 9 | 0,225 | 0,000150 | 0,0003170 | 0,0003 | 0,000150 | 0,027 | 0,000030 | 0,199 |
| 10 | 0,200 | 0,000147 | 0,0003298 | 0,0003 | 0,000147 | 0,027 | 0,000030 | 0,203 |
| 11 | 0,075 | 0,000109 | 0,0003975 | 0,0003 | 0,000109 | 0,027 | 0,000030 | 0,275 |

Рисунок 3.3 – Тарировочный график водомера Вентури, т.е. зависимость Qв= f(
 Нв)
Нв)
Рисунок 3.4 – Тарировочный график диафрагмы, т.е. зависимость Qд = f(
 Нд)
Нд)Общие выводы по выполненной работе:
В выполненной лабораторной работе мы ознакомились с общими законами гидродинамики трубопроводов: определение гидродинамических параметров потока движущейся жидкости при прохождении через измерительные приборы, представляющие местные сопротивления
В выполненной лабораторной работе был поставлен опыт в ходе которого была найдены перепады давления на диафрагме и водомере Вентури. По результатам опыта определили значение коэффициента расхода для водомера Вентури. По результатам расчетов построили тарировочные графики устройств.