Файл: Цель работы ознакомиться и понять смысл уравнения Бернулли, уметь применять его для решения практических задач гидродинамики. Схема лабораторной установки.docx

.

Изменение энергии по длине потока удобно проследить на графиках. Из уравнения Бернулли для потока реальной жидкости(закона сохранения энергии) видно, что гидродинамическая линия для потока реальной жидкости (с одним источником энергии) всегда ниспадающая. То же справедливо и для пьезометрической линии, но только в случае равномерного движения, когда скоростной напор   а уменьшение напора происходит только за счёт изменения потенциальной энергии потока, главным образом за счёт уменьшения давления P.

7. 
   Гидродинамическая трубка Пито предназначена для определения местных скоростей (осредненных во времени) в точках живого сечения безнапорного потока жидкости .
   

Трубка Пито, впервые примененная в 1732 г. французским инженером-гидротехником А. Пито, представляет собой изогнутую под прямым углом трубку, устанавливаемую открытым концом отогнутой части навстречу потоку так, чтобы центр отверстия трубки совпал с точкой потока, в которой определяется скорость движения жидкости. Второй, верхний, конец трубки выводится из потока наружу.

8. 
   Удельная энергия вдоль потока жидкости изменяется. Если считать, что изменение ее равномерно идет вдоль потока, иногда можно потерю энергии изобразить прямыми линиями и получить геометрическую, пьезометрическую и напорную линии (см.конспект лекции).
   

 

Геометрический уклон:

 

I = (Z₁ – Z₂)/l_1-2 (2.2)

есть тангенс угла наклона геометрической линии между сечениями к горизонтальной плоскости. Геометрический уклон показывает потерю удельной энергии положения, приходящейся на единицу длины:

Пьезометрический уклон:

 

J_p =((Z₁ + P₁/γ) – (Z₂ + P₂/γ))/l_1-2 .(2.3)

Пьезометрический уклон показывает потерю удельной потенциальной энергии, приходящейся на единицу длины.

Гидравлический уклон:

 

J = h_k/l_1-2 = (H₁ – H₂)/l_1-2 =(2.4)

=((Z₁ + P₁/γ +α₁υ₁²/(2g)) – (Z₂ + P₂

---

/γ + α₂υ₂²/(2g)))/l_1-2 .

Гидравлический уклон показывает потерю полной удельной энергии, приходящейся на единицу длины.

9. 
   Пьезометрическая линия характеризует изменение удельной потенциальной энергии, на сужающихся участках понижается, на расширяющихся повышается, а на участках с постоянным сечением проходит горизонтально (если речь идет об идеальном движении без потерь энергии) или со снижением, вызванным гидравлическими потерями (если речь идет о вязкой жидкости). Пьезометрическая линия отображает изменение статического напора.
   

Напорная линия характеризует изменение суммарной удельной энергии, для идеального движения жидкости (без потерь энергии) проходит горизонтально, для вязкой жидкости снижается за счет гидравлических потерь.Напорная линия отображает изменение полного напора.

Напорную и пьезометрические линии, как правило, строят в координатной плоскости совмещенной с принципиальной схемой гидросистемы.

10. 
    Уравнение Бернулли для струйки жидкости формулируется следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.
    

Уравнение Бернулли выглядит так:



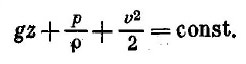
Подробное описание всех входящих в состав уравнения параметров уже описан в этой статье.

---