Файл: Постановка задачи синтеза электрического фильтра 2 Выбор.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 114
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Постановка задачи синтеза электрического фильтра
2. Аппроксимация частотной характеристики
рабочего ослабления фильтра по Чебышеву.
3. Реализация схемы ФНЧ по Попову.
4. Денормирование и расчет элементов схемы.
5. Расчет характеристик заданного фильтра.
Оглавление:
Оглавление: 1
Введение 2
Постановка задачи синтеза электрического фильтра 2
Выбор варианта 4
1.Нормирование по частоте 5
2. Аппроксимация частотной характеристики 5
рабочего ослабления фильтра по Чебышеву. 5
3. Реализация схемы ФНЧ по Попову. 8
4. Денормирование и расчет элементов схемы. 11
5. Расчет характеристик заданного фильтра. 11
6. Аналитический метод расчета характеристик фильтра 12
9. Выводы 19
10. Литература 19
Введение - 4 -
Постановка задачи синтеза электрического фильтра - 4 -
Выбор варианта - 6 -
1.Нормирование по частоте - 7 -
2. Аппроксимация частотной характеристики рабочего ослабления фильтра по Чебышеву. - 7 -
3. Реализация схемы ФНЧ по Попову. - 10 -
4. Денормирование и расчет элементов схемы. - 12 -
5. Расчет характеристик заданного фильтра. - 13 -
6. Аналитический метод расчета характеристик фильтра - 14 -
7. Расчет частотных характеристик фильтра на ЭВМ. - 15 -
8. Расчет временных характеристик фильтра на ЭВМ. - 17 -
9. Выводы - 21 -
10. Литература - 21 -
Введение
В современных системах связи широко применяются электрические фильтры – линейные пассивные четырехполюсники с резко выраженной частотной избирательностью. Они обладают малым и приблизительно постоянным затуханием в полосе частот, называемой полосой пропускания (прозрачности), и достаточно большим затуханием вне этой полосы. Область большого затухания называется полосой задерживания (задерживания, непрозрачности). Применяются различные типы фильтров: LC-фильтры, активные RC-фильтры (АRC-фильтры), пьезоэлектрические, пьезокерамические, магнитострикционные, электромеханические, волноводные, цифровые фильтры, фильтры СВЧ и др. Причем, LC-фильтры занимают особое положение в силу ряда причин. Во-первых, эти фильтры широко применяются в различных частотных диапазонах. Во-вторых, для LC-фильтров существует хорошо разработанная методика расчета, и синтез большинства перечисленных выше фильтров во многом использует эту методику. Однако следует помнить, что они не обеспечивают хорошего разделения полосы пропускания (ПП) от полосы затухания (ПЗ); в области пропускания и затухания могут наблюдаться большие неравномерности частотной характеристики; очень сложно выполнить условие согласования фильтра с нагрузкой.
Задачей синтеза электрического фильтра является определение схемы фильтра, содержащей минимально возможное число элементов, которая удовлетворяла бы техническим требованиям.
В настоящее время используются две принципиально отличные методики расчета фильтров:
а) расчет по характеристическим параметрам;
б) расчет по рабочим параметрам (по рабочему ослаблению или рабочей фазовой постоянной).
Метод синтеза по рабочим параметрам позволяет получить электрический фильтр с меньшим числом элементов, чем расчет по характеристическим параметрам. Кроме того, метод расчета по рабочим параметрам является единственно возможным для RC-фильтров и, следовательно, является более общим методом. Также следует отметить, что расчет по рабочим параметрам требует большей точности вычислений, что вызывает необходимость применения ЭВМ.
Постановка задачи синтеза электрического фильтра
Синтез электрического фильтра по рабочим параметрам состоит из двух этапов: аппроксимации и реализации.
На этапе аппроксимации необходимо получить аналитическое выражение рабочей передаточной функции
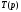 фильтра, удовлетворяющей условиям физической реализуемости по заданным требованиям.
фильтра, удовлетворяющей условиям физической реализуемости по заданным требованиям.На этапе реализации по найденной рабочей передаточной функции определяется схема фильтра и величины составляющих ее элементов.
В синтезе фильтров используется преобразование частоты и нормирование сопротивлений и частот.
Использование преобразования частоты позволяет свести расчет всех классов фильтров к расчету фильтра нижних частот (ФНЧ) и производить синтез любого фильтра в следующем порядке: сначала преобразовать заданную характеристику рабочего ослабления в низкочастотную, потом синтезировать ФНЧ, далее обратным частотным преобразованием перейти от элементов схемы ФНЧ к элементам (или их комбинациям) заданного фильтра.
Поэтому расчет любого фильтра начинается с расчета ФНЧ, нагруженного на нормированное сопротивление и с нормированной граничной частотой полосы пропускания, равной единице.
Техническими требованиями к фильтру являются:
- граничные частоты полосы пропускания (ПП) f2 или f2 , f21;
- граничные частоты полосы непропускания (ПН) f3 или f3 ,f31;
- максимально-допустимое значение рабочего ослабления в ПП ΔА (дБ) или коэффициент отражения ρ (%), которые связаны с соотношением:
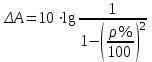
- минимально-допустимое значение рабочего ослабления в ПЗ Аmin (дБ);
- сопротивление нагрузки RН=R2 (Ом)
Между ПП и ПН находится переходная область, к которой никаких требований не предъявляется. Однако в этой полосе происходит нарастание рабочего ослабления от А до требуемой величины Аmin. Очевидно, при заданных А и Аmin, чем уже эта полоса, тем больше крутизна кривой ослабления фильтра в переходной и тем сложнее схема фильтра. И, наоборот, чем шире переходная полоса, тем проще схема фильтра.
Синтез электрического фильтра производится в следующем порядке:
-
Нормирование частот; -
Аппроксимация рабочей передаточной функции Т(р) и характеристики рабочего ослабления фильтра А(); -
Реализация схемы ФНЧ; -
Денормирование элементов схемы фильтра; -
Расчёт и построение денормированных частотных характеристик рабочего ослабления А(f) и рабочей фазы B(f) фильтра.
Выбор варианта
В соответствии с номером варианта, требуется рассчитать фильтр нижних частот (ФНЧ), удовлетворяющего следующим техническим требованиям:
-
Граничная частота полосы пропускания (ПП) f2 =1,8 кГц; -
Граничная частота полосы непропускания (ПН) f3 = 2,3 кГц; -
Минимально-допустимое значение рабочего ослабления в ПН Аmin =25 (дБ); -
Сопротивление нагрузки R2 =450 (Ом); -
Коэффициент отражения %
%
Аппроксимацию требуется выполнить по Чебышеву, а реализацию – упрощенным методом Попова.
\
1.Нормирование по частоте
Нормирование производим относительно граничной частоты полосы пропускания
f2 =1,8 кГц,
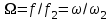 .
.Соответственно
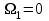 ,
, 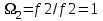 ,
, 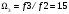 и
и 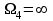 .
.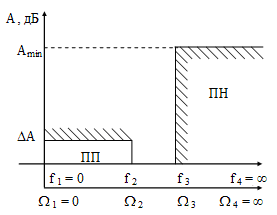
Рисунок 1.1 – Характеристика технических требований ФНЧ.
2. Аппроксимация частотной характеристики
рабочего ослабления фильтра по Чебышеву.
В качестве аппроксимирующих удобно использовать полиномиальные функции, среди которых наиболее широкое применение имеют полиномы Баттерворта и Чебышева.
При выборе полинома Чебышева в качестве аппроксимирующего функция фильтрации определяется выражением:
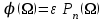 , где
, где 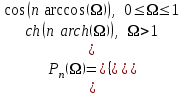 .
.0
 – коэффициент неравномерности рабочего ослабления в полосе пропускания.
– коэффициент неравномерности рабочего ослабления в полосе пропускания.Рабочее ослабление определяется как:
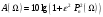 .
. 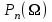 - полином Чебышева, определяемый рекуррентной формулой
- полином Чебышева, определяемый рекуррентной формулой 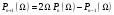 , n- порядок фильтра:
, n- порядок фильтра: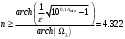
Округляя в большую сторону, возьмем
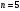 , тогда
, тогда 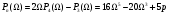 .
.Аппроксимация по Чебышеву получила название равноволновой.
Сформируем рабочую передаточную функцию:
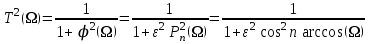 .
.С другой стороны модуль рабочей передаточной функции можно представить как:
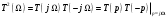 .
.Таким образом:
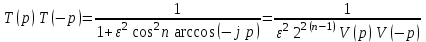 ,т.е.
,т.е. 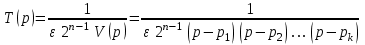 ,
,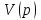 – полином Гурвица.
– полином Гурвица.Решая уравнение
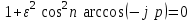 , определим корни полинома Гурвица:
, определим корни полинома Гурвица: 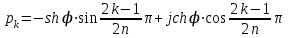 ,
, 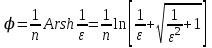 =0,2314
=0,2314Имеем:
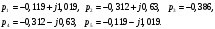
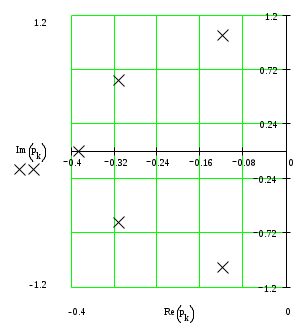
Рисунок 2.1 – Изображение корней уравнения
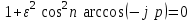 на комплексной плоскости
на комплексной плоскостиСформируем рабочую операторную передаточную функцию
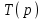
:
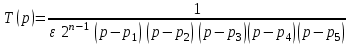
Подставляя
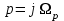 , определим рабочее ослабление как:
, определим рабочее ослабление как: 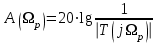 .
.Выполним проверку функции
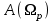 на частотах:
на частотах: 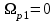 ,
, 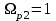 ,
, 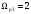 .
.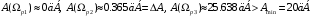
Аппроксимированное рабочее ослабление удовлетворяет техническим требованиям.
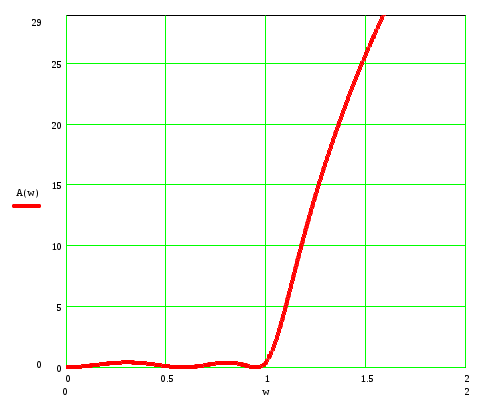
Рисунок 2.2 – График рабочего ослабления ФНЧ
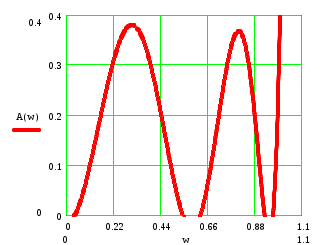
Рисунок 2.3 – График рабочего ослабления ФНЧ в ПП
Аппроксимация по Чебышеву даёт большую крутизну нарастания характеристики рабочего ослабления, чем аппроксимация по Баттерворту.. Чем выше порядок цепи, тем круче происходит нарастание рабочего ослабления. Аппроксимация по Чебышеву получила название равноволновой. Число экстремумов в ПП, включая граничные частоты, зависит от технических требований к фильтру и равно n+1.
3. Реализация схемы ФНЧ по Попову.
На данном этапе по найденной ранее функции
 необходимо получить схему фильтра нижних частот.
необходимо получить схему фильтра нижних частот.Существует несколько способов реализации электрических фильтров: по Дарлингтону, ускоренный метод реализации симметричных и антиметричных фильтров Попова, реализация по каталогу нормированных схем, структурная параметрическая и т.д. Согласно варианту будем проводить реализацию электрического фильтра по ускоренному методу Попова. Данный вид реализации основан на формировании функции
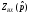 по
по 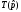 . Тогда получение схемы нагруженного фильтра можно свести к реализации двухполюсника путем разложения функции
. Тогда получение схемы нагруженного фильтра можно свести к реализации двухполюсника путем разложения функции