Файл: Постановка задачи синтеза электрического фильтра 2 Выбор.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 121
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Постановка задачи синтеза электрического фильтра
2. Аппроксимация частотной характеристики
рабочего ослабления фильтра по Чебышеву.
3. Реализация схемы ФНЧ по Попову.
4. Денормирование и расчет элементов схемы.
5. Расчет характеристик заданного фильтра.
 в цепную дробь (по Кауэру).
в цепную дробь (по Кауэру).Так как порядок фильтра нечетный, необходимо выполнить следующие действия:
-
Для каждой пары комплексно-сопряженных корней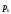 полинома
полинома 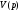 передаточной функции
передаточной функции  составим элементарный сомножитель
составим элементарный сомножитель 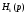 :
:
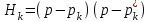 .
.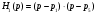
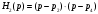
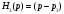
-
Сформируем полином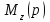 как произведение элементарных сомножителей с нечетными индексами:
как произведение элементарных сомножителей с нечетными индексами:
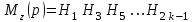 .
.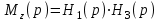
3. Сформируем полином
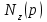 как произведение элементарных сомножителей с четными индексами:
как произведение элементарных сомножителей с четными индексами: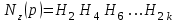 .
.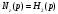
4. Составим функцию
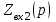 :
: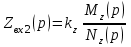 , где
, где 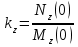 .
.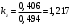
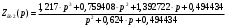
5. Разложим полученную функцию в цепную дробь по Кауэру и построим нормированную схему правой части фильтра.
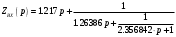 .
.Нормированные значения ёмкостей
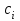 и индуктивностей
и индуктивностей 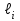 будут равны:
будут равны: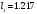 ,
, 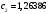 ,
, 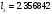 ,
, 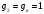
.
Построим нормированную схему правой половины фильтра:

Рисунок 3.1. – Нормированная схема правой половины фильтра.
П
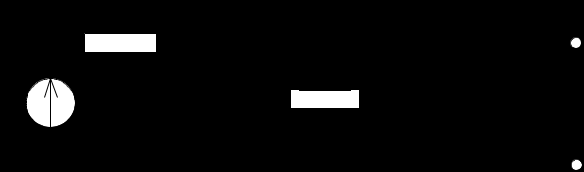
Рисунок 3.2. – Нормированная схема левой половины фильтра.
После объединения левой и правой половин, получим полную нормированную схему фильтра (рисунок 3.4).
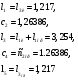
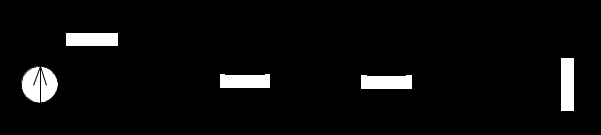
Рисунок 3.3. – Схема фильтра, полученная после объединения левой и правой частей.
Получим дуальную схему фильтра:
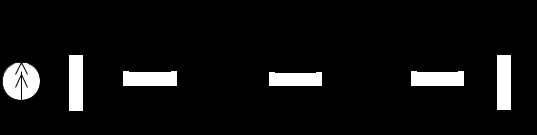
Рисунок 3.7. – Дуальная схема фильтра.
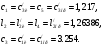
В общем случае, из двух выше приведённых схем для дальнейшего исследования выбирается более экономичная (с меньшим количеством индуктивностей в исходном фильтре). В данном примере выберем схему с источником тока.
4. Денормирование и расчет элементов схемы.
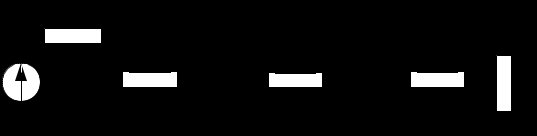
Рисунок 4.1 – Схема заданного фильтра
Для перехода от нормированной схемы к денормированной схеме с заданными нагрузочным сопротивлением R2 и граничной частотой f2 для ФНЧ осуществляется изменение уровня сопротивления и масштаба частоты с помощью следующих множителей:
а) преобразующий множитель сопротивления:
где R2 — нагрузочное сопротивление;
r2— нормированное нагрузочное сопротивление;
б) преобразующий множитель частоты:
Тогда коэффициенты денормирования индуктивности и ёмкости определятся по формулам:
и денормированные значения элементов схемы – с помощью:
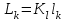 ,
, 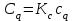
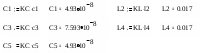
Величины емкостей приведены в фарадах, а индуктивностей в генри.
5. Расчет характеристик заданного фильтра.
После выполнения синтеза электрического фильтра важно убедиться в его соответствии техническим требованиям. Для этого разработчиком обязательно производится расчет частотных характеристик рабочего ослабления
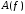 и рабочей фазы
и рабочей фазы 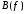 спроектированного фильтра, по которым проверяется выполнение технических требований:
спроектированного фильтра, по которым проверяется выполнение технических требований: а) рабочее ослабление в ПП не должно превышать заданной величины
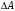 :
: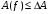
б) рабочее ослабление в ПН не должно быть ниже заданного значения
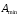 :
: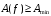
в) рабочая фаза
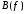 позволяет судить о выполнении требований к её линейности в пределах ПП.
позволяет судить о выполнении требований к её линейности в пределах ПП.Поставленная задача решается двумя способами:
1) аналитически, то есть расчётом
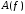 и
и 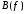 по полученной на этапе аппроксимации функции
по полученной на этапе аппроксимации функции 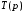 , чем проверяется правильность выполнения этапа аппроксимации.
, чем проверяется правильность выполнения этапа аппроксимации.2) расчетом частотных характеристик
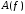 и
и 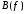
по операторной передаточной функции
 , полученной для разработанной на этапе реализации схемы фильтра заданным техническим условиям, то есть правильность синтеза фильтра в целом.
, полученной для разработанной на этапе реализации схемы фильтра заданным техническим условиям, то есть правильность синтеза фильтра в целом.6. Аналитический метод расчета характеристик фильтра
Расчет нормированных характеристик рабочего ослабления
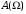 и рабочей фазы
и рабочей фазы 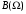 ФНЧ производим, пользуясь следующими соотношениями:
ФНЧ производим, пользуясь следующими соотношениями: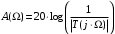
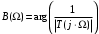
Зададимся частотами
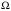 для расчета характеристик. Для фильтров Чебышева, имеющих равноволновый характер зависимостей
для расчета характеристик. Для фильтров Чебышева, имеющих равноволновый характер зависимостей 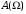 и
и 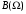 , произведем выбор пяти частот.
, произведем выбор пяти частот.Результаты расчета, проведенные в программе Mathcad 7, сведены в таблицу 6.1:
Таблица 6.1
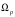 | 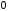 | 0,309 | 0,588 | 0,809 | 0,951 | 1 |
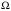 | 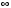 | 3,236 | 0,701 | 1,236 | 1,052 | 1 |
| | 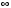 | 2.101 | 3.998 | 5.502 | 6.467 | 6.8 |
| | 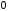 | 0.39 | 0 | 0.4 | 0 | 0.399 |
| |  | 61,633 | 120,878 | 174,177 | -144.364 | -126.288 |
Проверка технических требований по таблице 6.1 подтверждает соответствие аппроксимированной
 техническому заданию.
техническому заданию.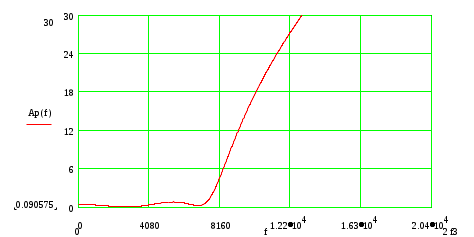
Рисунок 6.1. – График зависимости рабочего ослабления фильтра.
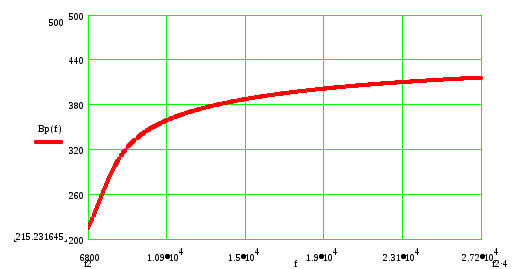
Рисунок 6.2 – График зависимости рабочей фазы фильтра.
7. Расчет частотных характеристик фильтра на ЭВМ.
Сделаем проверку правильности расчета спроектированного фильтра. Для этого рассчитаем частотные зависимости
 и
и  по передаточной функции
по передаточной функции  , выраженной через элементы фильтра.
, выраженной через элементы фильтра.Рабочая передаточная функция нашего фильтра может быть определена следующим образом:
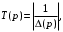
где
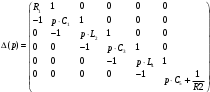
континуант, записанный в операторном виде для ускорения расчетов.
Рабочее ослабление и рабочая фаза рассчитываются в соответствии с выражениями:
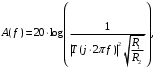
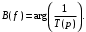
Ниже представлены графики данных зависимостей:

Рисунок 7.1. – График зависимости рабочего ослабления фильтра.

Рисунок 7.2. – График зависимости рабочей фазы синтезируемого фильтра.
Как видно из графиков и данных вычислений, требования к фильтру выполняются.
8. Расчет временных характеристик фильтра на ЭВМ.
Для вычисления переходной характеристики использовано следующее выражение:
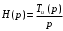
При использовании специальной функции, выполняющей обратное преобразование Лапласа (в системе Mathcad 7 в нашем случае эта функция записывается как