Файл: Лабораторная работа 1. Определение земного ускорения свободного падения при помощи оборот ного и математического маятников.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 191
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
которые наблюдаются в случае, когда выпуклая поверхность линзы малой кривизны соприкасается с плоской поверхностью хорошо отполированной пластины (рис. 3).
При этом остающаяся между ними воздушная прослойка постепенно утолщается от центра к краям. Параллельный пучок света, падая на такую оптическую систему, отражается от стеклянных поверхностей, формирующих воздушный круговой клин, и образует когерентные световые пучки, которые при интерференции дают систему светлых и темных колец Ньютона.
Кольца Ньютона можно наблюдать как в отраженном свете (рис. 3,а), так и в проходящем свете (рис. 3,б).




 Пусть наблюдение ведется со стороны линзы.
Пусть наблюдение ведется со стороны линзы.

 С этой же стороны на линзу падает пучок монохроматического света. Тогда световые
С этой же стороны на линзу падает пучок монохроматического света. Тогда световые




 волны, отраженные от верхней и нижней
волны, отраженные от верхней и нижней
границ воздушной прослойки, будут
 интерферировать между собой. В результате
интерферировать между собой. В результате
получится следующая картина: в центре

 расположено темное пятно, окруженное
расположено темное пятно, окруженное
 рядом концентрических светлых и темных
рядом концентрических светлых и темных

 колец убывающей ширины. При малых
колец убывающей ширины. При малых
размерах интерференционной картины
(порядка нескольких миллиметров)
наблюдение ведется через микроскоп.
Рис. 3, а











Если световой пучок падает со стороны
 пластины, а наблюдение по-прежнему
пластины, а наблюдение по-прежнему

 ведется со стороны линзы, то
ведется со стороны линзы, то

 интерференционная картина останется
интерференционная картина останется

 прежней с той лишь разницей, что пятно
прежней с той лишь разницей, что пятно
в центре будет светлым, все светлые
кольца заменятся темными, а темные -
светлыми.
Рис. 3, б
В нашем случае кольца Ньютона образуются в оптической системе,
состоящей из двух линз (рис. 4).


R1


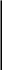


R2 RRRRR

 bk h
bk h
 ak
ak
rk O

Рис. 4
Пусть мы имеем две линзы с радиусами кривизны R1 и R2, причем R1 R2.
Эти две линзы соприкасаются друг с другом в точке О.
Обозначим зазор между линзами в том месте, где наблюдается К-ое кольцо Ньютона bk. Найдем величину воздушного зазора bk. Рассмотрим сначала треугольник, гипотенуза которого R2
R22 = rk2 + (R2 – h)2, где h = bk + ak
или
R22 = rk2 + R22 – 2R2h + h2.
Задачу решаем в 1-ом приближении с точностью до h2, тогда
rk2 = 2R2h
или
rk2 = 2R2(bk + ak). (4)
Теперь рассмотрим другой треугольник с гипотенузой R1:
R12 = rk2 + (R1 – ak)2
R12 = rk2 + R12 – 2R1ak + ak2, ak2 пренебрегаем,
тогда
rk2 = 2R1ak (5)
Отсюда выразим ak: ak = rk2 / 2R1
И подставим в выражение (4).
Тогда
rk2 =2R2(bk + rk2 / 2R1),
Откуда
bk = rk2 (1 - R2 / R1) / 2R2 (6)
Разность хода лучей, отраженных от верхней и нижней граней воздушной прослойки bk равна:
= 2bk + /2, где /2 – потеря полволны при отражении на границе воздух-линза (с радиусом R1).
Если эта разность хода равна = (2k + 1)/2, то мы наблюдаем темное кольцо:
2bk + /2 = (2k + 1)/2 (7)
Подставим bk из (6) в выражение (7) :
rk2 (1 - R2 / R1) / R2 + /2 = (2k + 1)/2 (8)
Так как две линзы вследствие упругой деформации могут соприкасаться не в одной точке О, то расчеты будем проводить по разности квадратов двух колец.
rn2 (1 - R2 / R1) / R2 + /2 = (2n + 1)/2 (9)
Вычтем (9) почленно из уравнения (8), получим
R2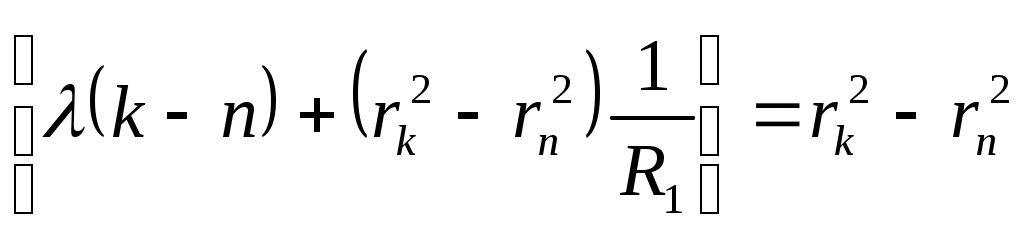 . (10)
. (10)
Отсюда можно определить радиус второй линзы R2:
R2 =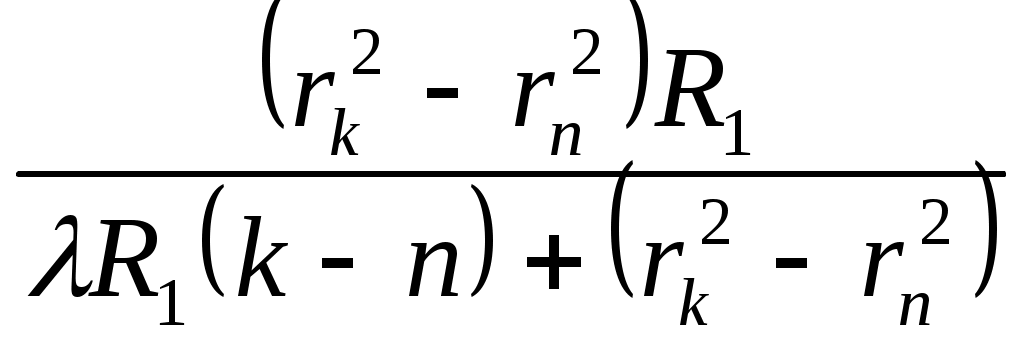 (11)
(11)
Измерив радиусы двух колец Ньютона
k и n (номера колец), можно рассчитать радиус меньшей линзы R2.
R1 = 113 мм.
ОПИСАНИЕ УСТАНОВКИ.
Установка, используемая для наблюдения колец Ньютона, изображена на рисунке 5.
На штативе 1 с помощью винта 2 крепится столик 3. На столике 3 в металлической оправе 4 помещены две сферические линзы 5 и 6. Тремя установочными винтами 7 регулируется положение линз относительно друг друга, а, следовательно, и величина зазора воздушного кругового клина, образованного сферическими поверхностями линз.
Над системой линз, под углом 450 укреплена полупрозрачная пластинка 8, направляющая свет на линзы. Интерференционная картина наблюдается в микроскоп 9 с окулярной шкалой (окулярный микрометр), цена деления которой 0,1 мм. Тубус микроскопа перемещается по высоте поворотом металлического кольца 10. Перемещение окуляра микроскопа осуществляется вращением накатного кольца 11. Источником света служит электрическая лампочка, помещенная в кожух 12, в передней части которого установлен диск светофильтров 13.
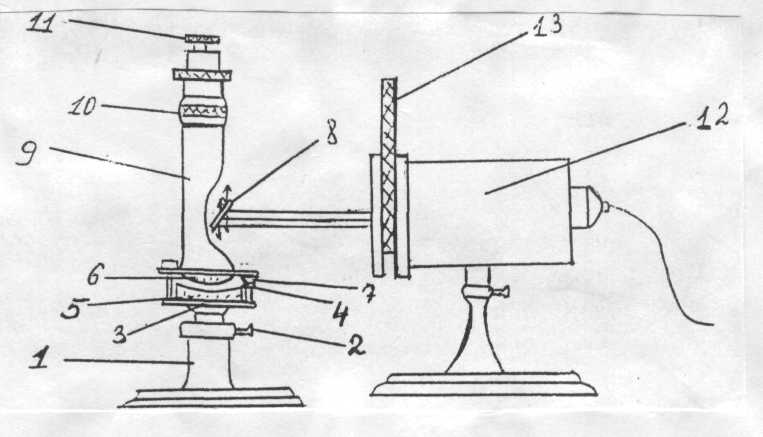
Рис. 5.
Принципиальная оптическая схема установки дана на рис. 6. Свет от источника проходит светофильтр К и падает на полупрозрачную пластинку М. Отразившись от пластинки М, свет идет на систему линз. В результате интерференции лучей, отраженных от верхней и нижней границ воздушного клина, образуются кольца Ньютона, которые рассматриваются с помощью микроскопа.

 OK
OK


 ОБ К
ОБ К


 M S
M S
L2


 L1
L1

Рис. 6.
ВЫПОЛНЕНИЕ РАБОТЫ.
Задание 1. Определение радиуса кривизны линзы.
Таблица 1.
Внимание! Кольца не сбивать! Установочные винты не крутить!
7. Вычислить радиус кривизны по формуле ( 11) . R1= 113 мм, = 546 нм.
Для уменьшения погрешности при расчете не брать радиусы соседних колец.
Задание 2. Определение длины световой волны.
При этом остающаяся между ними воздушная прослойка постепенно утолщается от центра к краям. Параллельный пучок света, падая на такую оптическую систему, отражается от стеклянных поверхностей, формирующих воздушный круговой клин, и образует когерентные световые пучки, которые при интерференции дают систему светлых и темных колец Ньютона.
Кольца Ньютона можно наблюдать как в отраженном свете (рис. 3,а), так и в проходящем свете (рис. 3,б).




 Пусть наблюдение ведется со стороны линзы.
Пусть наблюдение ведется со стороны линзы. 
 С этой же стороны на линзу падает пучок монохроматического света. Тогда световые
С этой же стороны на линзу падает пучок монохроматического света. Тогда световые



 волны, отраженные от верхней и нижней
волны, отраженные от верхней и нижней границ воздушной прослойки, будут
 интерферировать между собой. В результате
интерферировать между собой. В результате получится следующая картина: в центре

 расположено темное пятно, окруженное
расположено темное пятно, окруженное рядом концентрических светлых и темных
рядом концентрических светлых и темных 
 колец убывающей ширины. При малых
колец убывающей ширины. При малых 
размерах интерференционной картины
(порядка нескольких миллиметров)
наблюдение ведется через микроскоп.
Рис. 3, а











Если световой пучок падает со стороны
 пластины, а наблюдение по-прежнему
пластины, а наблюдение по-прежнему
 ведется со стороны линзы, то
ведется со стороны линзы, то 
 интерференционная картина останется
интерференционная картина останется 
 прежней с той лишь разницей, что пятно
прежней с той лишь разницей, что пятно в центре будет светлым, все светлые
кольца заменятся темными, а темные -
светлыми.
Рис. 3, б
В нашем случае кольца Ньютона образуются в оптической системе,
состоящей из двух линз (рис. 4).


R1


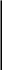


R2 RRRRR

 bk h
bk h ak
ak rk O

Рис. 4
Пусть мы имеем две линзы с радиусами кривизны R1 и R2, причем R1 R2.
Эти две линзы соприкасаются друг с другом в точке О.
Обозначим зазор между линзами в том месте, где наблюдается К-ое кольцо Ньютона bk. Найдем величину воздушного зазора bk. Рассмотрим сначала треугольник, гипотенуза которого R2
R22 = rk2 + (R2 – h)2, где h = bk + ak
или
R22 = rk2 + R22 – 2R2h + h2.
Задачу решаем в 1-ом приближении с точностью до h2, тогда
rk2 = 2R2h
или
rk2 = 2R2(bk + ak). (4)
Теперь рассмотрим другой треугольник с гипотенузой R1:
R12 = rk2 + (R1 – ak)2
R12 = rk2 + R12 – 2R1ak + ak2, ak2 пренебрегаем,
тогда
rk2 = 2R1ak (5)
Отсюда выразим ak: ak = rk2 / 2R1
И подставим в выражение (4).
Тогда
rk2 =2R2(bk + rk2 / 2R1),
Откуда
bk = rk2 (1 - R2 / R1) / 2R2 (6)
Разность хода лучей, отраженных от верхней и нижней граней воздушной прослойки bk равна:
= 2bk + /2, где /2 – потеря полволны при отражении на границе воздух-линза (с радиусом R1).
Если эта разность хода равна = (2k + 1)/2, то мы наблюдаем темное кольцо:
2bk + /2 = (2k + 1)/2 (7)
Подставим bk из (6) в выражение (7) :
rk2 (1 - R2 / R1) / R2 + /2 = (2k + 1)/2 (8)
Так как две линзы вследствие упругой деформации могут соприкасаться не в одной точке О, то расчеты будем проводить по разности квадратов двух колец.
rn2 (1 - R2 / R1) / R2 + /2 = (2n + 1)/2 (9)
Вычтем (9) почленно из уравнения (8), получим
R2
Отсюда можно определить радиус второй линзы R2:
R2 =
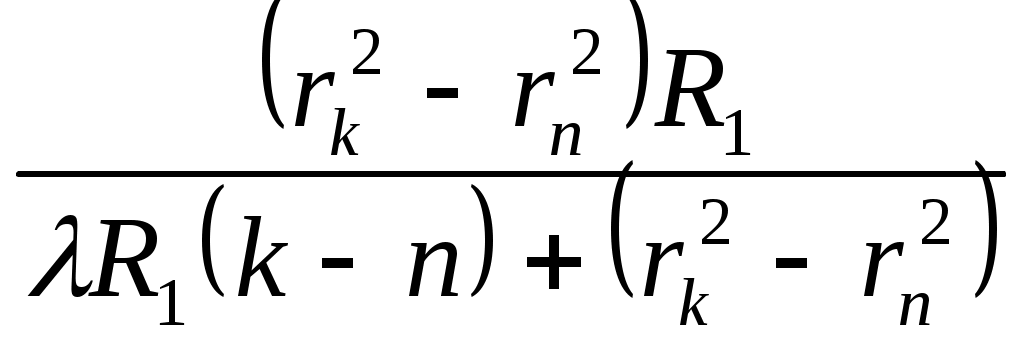 (11)
(11) Измерив радиусы двух колец Ньютона
k и n (номера колец), можно рассчитать радиус меньшей линзы R2.
R1 = 113 мм.
ОПИСАНИЕ УСТАНОВКИ.
Установка, используемая для наблюдения колец Ньютона, изображена на рисунке 5.
На штативе 1 с помощью винта 2 крепится столик 3. На столике 3 в металлической оправе 4 помещены две сферические линзы 5 и 6. Тремя установочными винтами 7 регулируется положение линз относительно друг друга, а, следовательно, и величина зазора воздушного кругового клина, образованного сферическими поверхностями линз.
Над системой линз, под углом 450 укреплена полупрозрачная пластинка 8, направляющая свет на линзы. Интерференционная картина наблюдается в микроскоп 9 с окулярной шкалой (окулярный микрометр), цена деления которой 0,1 мм. Тубус микроскопа перемещается по высоте поворотом металлического кольца 10. Перемещение окуляра микроскопа осуществляется вращением накатного кольца 11. Источником света служит электрическая лампочка, помещенная в кожух 12, в передней части которого установлен диск светофильтров 13.

Рис. 5.
Принципиальная оптическая схема установки дана на рис. 6. Свет от источника проходит светофильтр К и падает на полупрозрачную пластинку М. Отразившись от пластинки М, свет идет на систему линз. В результате интерференции лучей, отраженных от верхней и нижней границ воздушного клина, образуются кольца Ньютона, которые рассматриваются с помощью микроскопа.

 OK
OK

 ОБ К
ОБ К 


 M S
M SL2


 L1
L1 
Рис. 6.
ВЫПОЛНЕНИЕ РАБОТЫ.
Задание 1. Определение радиуса кривизны линзы.
-
Включить осветительную лампу в сеть. -
Ввести зеленый светофильтр, вращая диск светофильтров. -
Проверить, на одной ли высоте находятся полупрозрачная пластинка 8 и осветитель. В противном случае, ослабив винт 2, отрегулировать по высоте столик 3. -
Наблюдая в микроскоп, с помощью установочных винтов 7 ввести кольца в поле зрения. Расположить их так, чтобы шкала проходила по их диаметру. -
Сфокусировать микроскоп поворотом металлического кольца 10 и накатного кольца 11, добиваясь хорошей видимости колец и шкалы окуляра. -
Измерить по шкале местоположение концов диаметров как минимум 4-х темных колец (цена деления 0,1 мм). Полученные результаты для всех колец занести в таблицу 1.
Таблица 1.
| Номер кольца | Число измерений | Положение на шкале концов диаметров колец | D= a-b | r | |
| | | a | b | | |
| 1 | 1,2,3 среднее | | | | |
| 2 | ... | | | | |
| 3 | ... | | | | |
| 4 | ... | | | | |
Внимание! Кольца не сбивать! Установочные винты не крутить!
7. Вычислить радиус кривизны по формуле ( 11) . R1= 113 мм, = 546 нм.
Для уменьшения погрешности при расчете не брать радиусы соседних колец.
Задание 2. Определение длины световой волны.
-
Вращая диск светофильтров, ввести красный светофильтр. -
Измерить радиусы колец, аналогично описанному в упражнении 1. -
Построить таблицу 2 (аналогично приведенной таблице 1, заменив R на ) и внести в нее все измеренные и рассчитанные величины. -
По формуле