Файл: Лабораторная работа 1. Определение земного ускорения свободного падения при помощи оборот ного и математического маятников.doc

Лабораторная работа №1.
Определение земного ускорения свободного падения

при помощи оборотного и математического маятников.

Цель работы: экспериментально определить ускорение свободного падения с помощью физического и математического маятников. Оборудование и принадлежности: установка с физическим и математическим маятником, секундомер, линейка с миллиметровыми делениями. 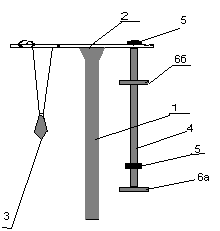Рис.1. Схематический рисунок установки

ОПИСАНИЕ УСТАНОВКИ.

Общий вид оборотного маятника показан на рис.1. На стойке 1 зафиксирован кронштейн 2, на котором закреплён математический маятник 3 и оборотный маятник 4.

Оборотный маятник выполнен в виде стального стержня, на котором фиксируются две повернутые лезвиями друг к другу опорные призмы 5 и две чечевицы (подвижная 6а и неподвижная 6б).

На стержне с одного конца через 10 мм нанесены углубления. Подвижную чечевицу можно перемещать вдоль стержня и фиксировать в любом положении.

ЭЛЕМЕНТЫ ТЕОРИИ.



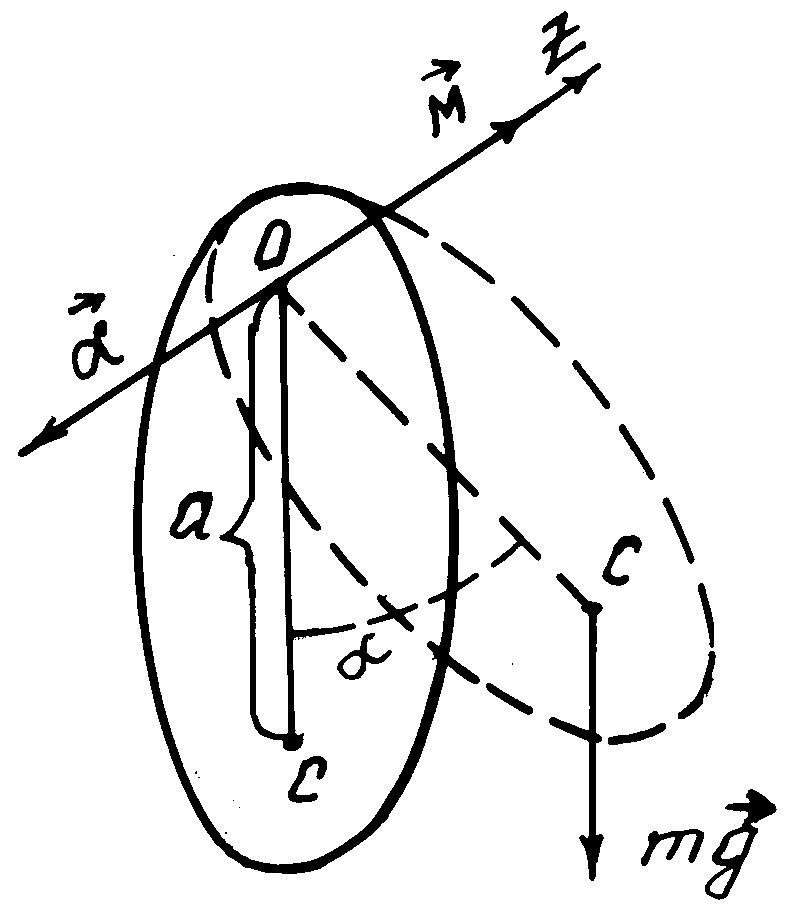
Рис. 2
Общие сведения. Физическим маятником называется твердое тело, способное совершать колебания под действием силы тяжести относительно горизонтальной оси, не проходящей через центр массы (рис. 2). К таким колебаниям применимо основное уравнение динамики вращательного движения твёрдого тела, которое в проекции на ось вращения Z имеет вид:

(1)

где M_z – проекция момента силы тяжести на осьZ, I – момент инерции маятника относительно оси колебаний, _z – проекция углового ускорения на ось Z. Учитывая, что M_z = –mgasin, _z = d²/dt², получим:


, (2)

где m – масса маятника, a – расстояние от оси вращения до центра масс маятника,

---

 – угловое перемещение маятника (угол отклонения маятника от положения равновесия). Угловое перемещение – векторная величина, его направление определяется по правилу буравчика. В данном случае векторы и направлены в противоположные стороны, поэтому выражение для M_z записано со знаком минус.

При малых углах отклонения sin, в этом случае уравнение (2) можно записать в виде:

+ (3)

Уравнение (3) представляет собой уравнение гармонических колебаний переменной величины , квадрат угловой частоты которых равен коэффициенту перед  во втором слагаемом. То есть

(4)

Решение уравнения (3) можно записать в виде

(t) = _ocos(t + _o), (5)

где _o – угловая амплитуда колебаний, _o – начальная фаза колебаний.

Из вышеизложенного следует, что колебания физического маятника (как и математического маятника) не являются гармоническими. Они будут мало отличаться от гармонических колебаний лишь в том случае, когда выполняется условие sin, то есть, когда угол отклонения маятника от положения равновесия небольшой.

Из формулы (4) находим период колебаний физического маятника:

(6)

Период колебаний математического маятника длиной L вычисляется по формуле:

(7)

Сравнивая формулы (6) и (7), приходим к выводу, что математический маятник, длина которого

, (8)

будет совершать колебания с тем же периодом, что и данный физический маятник. Точка, находящаяся на расстоянии L (рис. 1) от оси вращения физического маятника на прямой, проходящей через его центр масс перпендикулярно оси вращения, называется центром качания физического маятника. Величина L, вычисляемая по формуле (8), называется приведенной длиной физического маятника.

---

По теореме Гюйгенса – Штейнера

I = I_o + ma², (9)

где I_o – момент инерции физического маятника относительно оси, проходящей через его центр масс параллельно оси колебаний.

Подставив (9) в (8), получим:

(10)



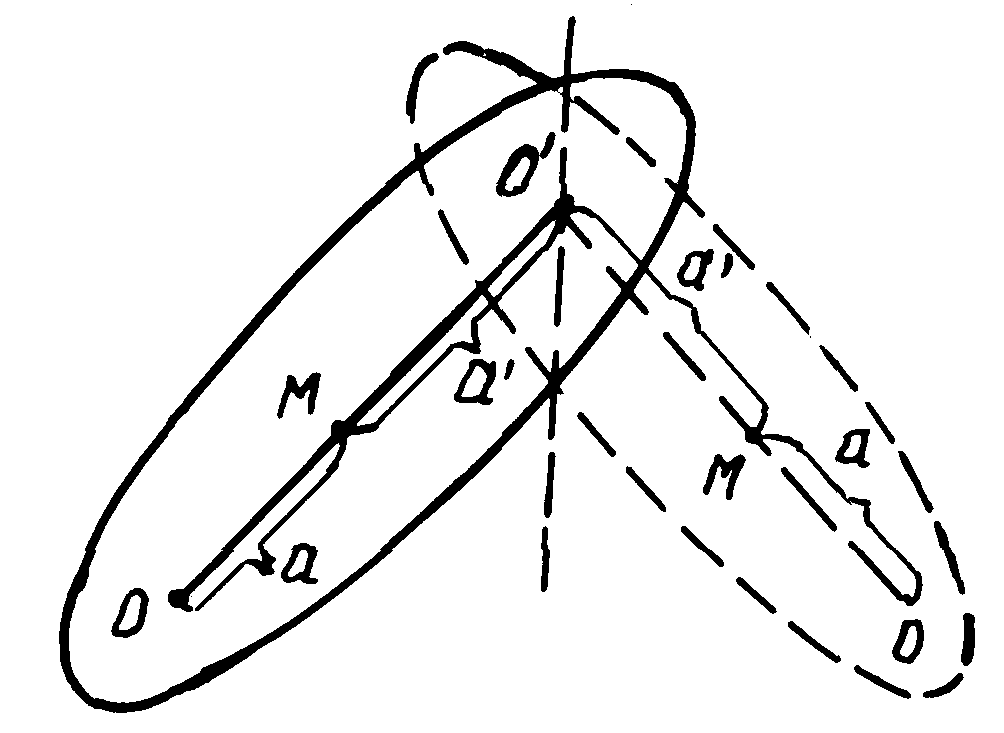
Рис. 3

Из (10) следует, что приведенная длина физического маятника больше расстояния от оси вращения до центра масс маятника на величину (рис. 2, 3)

. (11)

Подвесим маятник на оси, параллельной прежней и проходящей через центр качания О (рис. 3). В этом случае приведенная длина маятника

(12)

По теореме Гюйгенса – Штейнера Подставив это выражение в (12), а также учитывая, что a₁ = I_o/ma = L - a, получим:

.

Так как приведенная длина физического маятника относительно новой оси не изменилась, то и период его колебаний на новой оси также не изменился. Следовательно, данная ось и параллельная ей ось, проходящая через центр качания маятника, обладают свойством взаимности.

Ускорение свободного падения можно вычислить по формуле

. (13)

При определении ускорения свободного падения с помощью оборотного маятника необходимо, изменяя его момент инерции (передвигая чечевицу 6а), добиться того, чтобы расстояние между опорными призмами стало равным приведенной длине оборотного маятника. Измерив L и T, по формуле (13) находим g.

Для определения ускорения свободного падения с помощью математического маятника необходимо измерить его длину L, соответствующий ей период колебаний T, и по формуле (13) вычислить g.

Чтобы повысить точность измерения периода колебаний T, необходимо измерить время t для n колебаний (обычно n = 10). Тогда

. (14)
Порядок выполнения задания 1

1. Установить чечевицу 6а на расстоянии d

---

= 1 см от конца маятника.

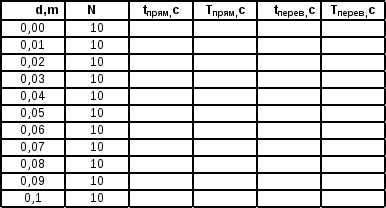
2. Пользуясь секундомером, определить t (время n колебаний маятника), передвигая чечевицу 6а каждый раз на 1 см в диапазоне 1 – 15 см, в прямом и перевернутом положениях маятника для каждого положения передвигаемой чечевицы 6а. По формуле (14) найти период колебания. Данные занести в таблицу 1.

Таблица 1.

Результаты измерений периодов колебаний оборотного маятника.


3. На одном чертеже построить графики T(d) зависимости периодов колебаний в прямом и перевернутом положениях маятника от расстояния чечевицы 6а от конца стержня. Точка пересечения графиков будет соответствовать равенству периодов этих колебаний.

4. Установить чечевицу 6а в положение, соответствующее равенству периодов колебаний, и проверить их совпадение. Если T_прям. = T_перев., то расстояние между опорными призмами равно приведенной длине L оборотного маятника.

5. Провести n раз измерения величин L, T, входящих в правую часть равенства (13), определить средние значения и .

6. По формуле (13) определить среднее значение ускорения свободного падения <g>.
Порядок выполнения задания 2.

1. Определить период Т колебаний математического маятника при различной его длине L. Для этого, как и в первом задании, измерить время t для n = 10 колебаний и найти T по формуле (14). Данные занести в таблицу 2.

2. По формуле (13) определить ускорение свободного падения g.

Таблица 2

Результаты измерений и расчётов ускорения свободного падения

с помощью математического маятника.


3. Построить график L (T² ).

4. Сравнить значения ускорения свободного падения, полученные в первом и во втором заданиях.

На основании проделанных измерений сформулировать цель работы и сделать выводы.

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1. Что такое физический и математический маятники ?

2. Дать определение физических величин: момент силы, момент инерции.

3. Какие колебания называются гармоническими? Привести примеры.

4. Что такое центр качания, как он расположен по отношению к точке

подвеса?

ЛИТЕРАТУРА:

1. Матвеев А.Н. Механика и теория относ-сти. -М.: Высшая школа, 1986;

2. Трофимова Т.И. Курс физики. -М.: Высшая школа, 1997;

3.Сивухин Д.В. Общий курс физики. -М.: Наука, 1989 Т. 1. Механика;

4. Физический практикум. Под ред. Кембровского Г.С. -Минск: Изд-во "Университетское", 1986.

Лабораторная работа №2

СЛОЖЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
Цель работы: Изучить биения и сложение двух взаимно перпендикулярных колебаний с помощью электронного осциллографа.

Оборудование и принадлежности: осциллограф универсальный

С1-65, звуковой генератор, соединительные провода.
ЭЛЕМЕНТЫ ТЕОРИИ
Колебаниями называются движения или процессы, обладающие той или иной повторяемостью во времени. Простейшим типом колебаний являются гармонические колебания – колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса) и описываются уравнением типа

x = А соs (t + ₀),

где А – максимальное значение колеблющейся величины, называемое амплитудой колебания,  – круговая (циклическая) частота, ₀ или ₀ – начальная фаза колебания в момент t=0, (t + ₀) – фаза колебания в момент времени t. Фаза колебания определяет значение колеблющейся величины в данный момент времени. Так как косинус изменяется в пределах от +1 до –1, то х может принимать значения от +А до –А.

Определенные состояния системы, совершающей гармонические колебания, повторяются через промежуток времени Т, называемой периодом колебания, за который фаза колебания получает приращение 2.

Т= 2

Величина, обратная периоду колебаний,  = 1/Т называется частотой колебаний и равна числу полных колебаний, совершаемых в единицу времени. Откуда =2. Единица частоты  - герц (Гц). 1 Гц – частота периодического процесса, при которой за 1 с совершается 1 цикл процесса.

Гармонические колебания могут изображаться графически методом вращающегося вектора амплитуды, или методом векторных диаграмм.
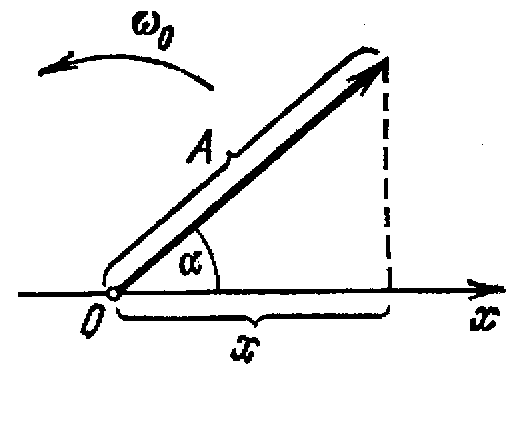Возьмем ось, вдоль которой будем откладывать колеблющуюся величину x(рис.1). Из взятой на оси точки О отложим вектор длины A, образующий с осью угол . Если привести этот вектор во вращение с угло­вой скоростью ω, то проекция конца вектора будет перемещать­ся по оси x в пределах от -А до +A, причем координата этой проекции будет изменяться со временем по закону

Рис. 1.


Следовательно, проекция конца вектора на ось будет совершать гармонические колебания с ам­плитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с на­чальной фазой, равной углу, образуемому вектором с осью в начальный момент времени.

Таким образом, гармоническое колебание может быть задано с помощью вектора, длина которого рав­на амплитуде колебания, а направление образует с осью x угол, равный начальной фазе колебаний.

Рассмотрим сложение двух гармонических коле­баний одного направления и одинаковой частоты. Результирующее колебаниебудет суммой колеба­ний х₁и x₂, которые определяются функциями
, (1)
¯

П 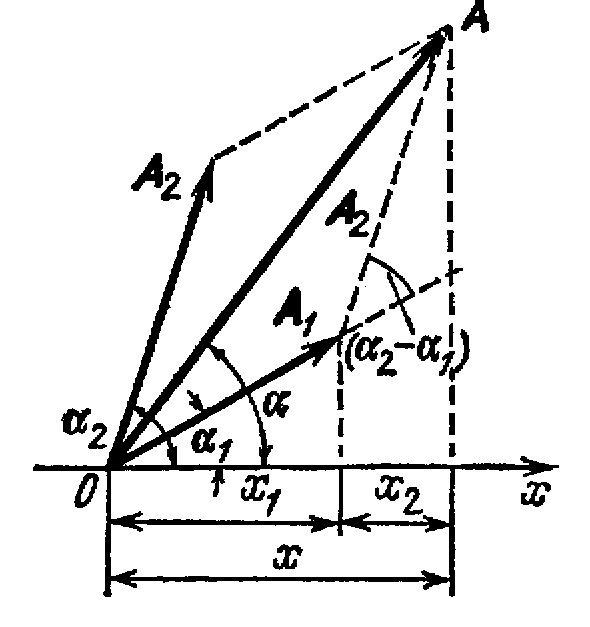редставим оба колебания с помощью векторов A₁и А₂ (рис.2). Построим по правилам сложения векторов результирующий вектор А. На рисунке вид­но, что проекция этого вектора на ось xравна сум­ме проекций складываемых векторов:



Поэтому вектор Aпредставляет собой резуль­тирующее колебание. Этот вектор вращается с той же угловой скоростью ω₀, как и векторы А₁и А₂, так что сумма x₁и х₂является гармоническим колебанием с

Рис. 2. частотой ω₀, амплитудой Aи начальной

фа­зой α.
Используя теорему косинусов получаем, что
(2)

Также из рисунка видно, что
(3)
Представление гармонических колебаний с помощью векторов позволяет заменить сложение функций сложением векторов, что значительно проще.
1. Биения.

Рассмотрим сложение двух гармонических колебаний, происходящих вдоль одной прямой с частотами ω₁ и ω₂, незначительно отличающихся друг от друга. (Ω=( |ω₁ - ω₂ |<< ω₁ и Ω<< ω₂ ).Пусть в начальный момент времени фазы складываемых колебаний одинаковы. Тогда эти колебания запишутся в виде
и (4)

Найдем сумму двух таких колебаний, предположив для простоты сначала, что их амплитуды одинаковы (A₁ = A₂): (5)







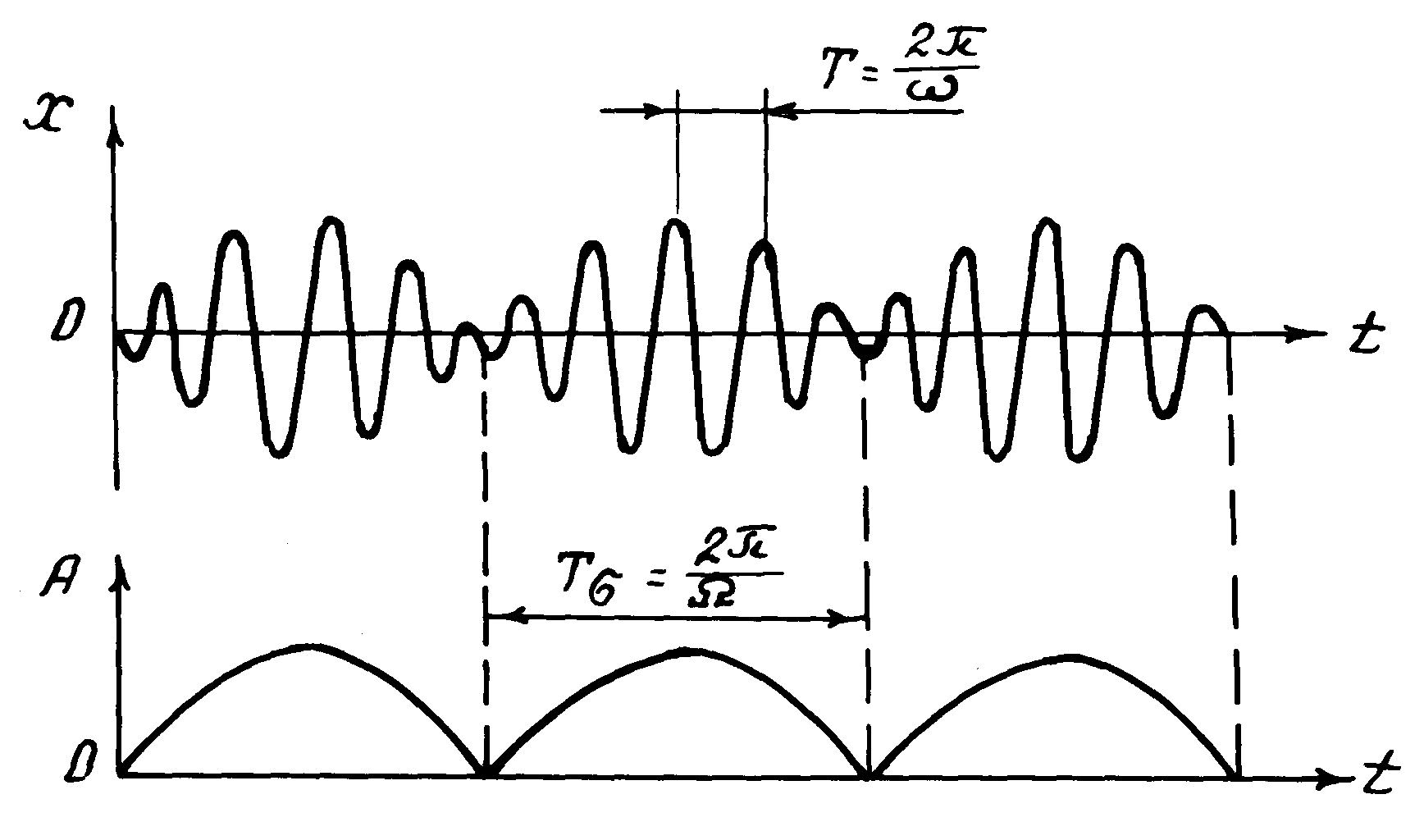
Рис. 3.

Отсюда видно, что результирующее колебание (биение) происходит с частотой (ω₁+ω₂)/2, а амплитуда колебаний со временем изменяется в пределах от 2A₁ до 0 по закону (рис. 3). Значение 2A₁ достигается тогда, когда фазы складываемых колебаний совпадают, а нуль - когда фазы противоположны. Периодическое изменение результирующей амплитуды, получающееся при сложении колебаний, совершающихся с близкими частотами и вдоль одной прямой, называют биениями. Циклическая частота биений Ω= |ω₁ - ω₂ |, период биений Т = 2π/ Ω (рис.3) и частота биений

ν_б = 1/T_б = |ν₁ - ν₂ |, где ν₁ и ν₂- частоты складываемых колебаний.




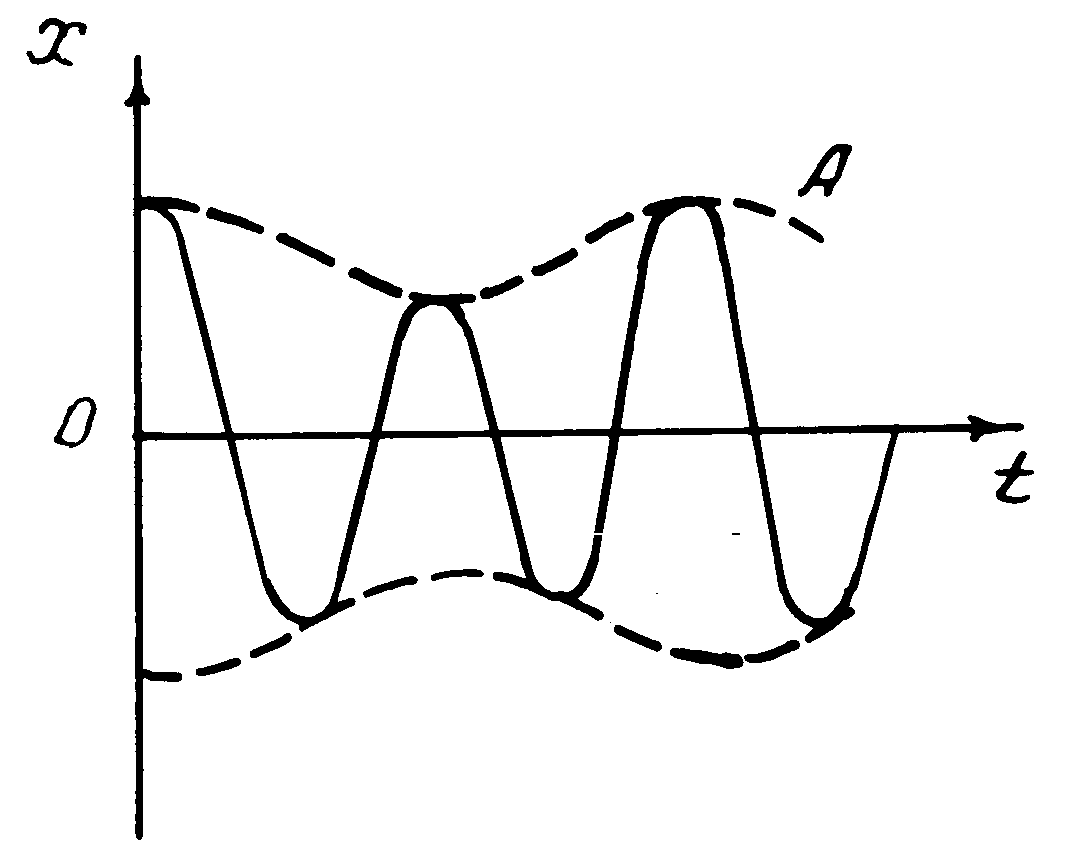
Рис. 4.

Если амплитуды складываемых колебаний не равны (A₁ # A₂), то максимальное значение амплитуды результирующего колебания равно A₁+A₂, а минимальное  А₁-А₂. В этом случае биения выражены менее четко (рис.4). Частоты Ω, ν_б и период T_б определяются разностью частот складываемых колебаний и не зависят от их амплитуд и начальных фаз.
Сложение колебаний во взаимно перпендикулярных направлениях.
Представим две взаимно перпен­дикулярные векторные величины xи y, изменяющие­ся со временем с одинаковой частотой ω по гармони­ческому закону

(6)

где e_xи e_у — орты координатных осей xи y, Аи B — амплитуды колебаний. Величинами xиуможет быть, например, смещения материальной точки (частицы) из положения равновесия. В случае колеблющейся частицы величины

, , (7)
определяют координаты частицы на плоскости xy. Частица будет двигаться по некоторой траектории, вид которой зависит от раз­ности фаз обоих колебаний. Выражения (6) пред­ставляют собой заданное в параметрической форме уравнение этой траектории. Чтобы получить уравне­ние траектории в обычном виде, нужно исключить из уравнений (6) параметр t. Из первого уравне­ния следует, что

(8)

Соответственно
(9)
Развернем косинус во втором из уравнений (6) по формуле для косинуса суммы:

Подставим вместо cosωtи sinωt их значения (3) и (4):


Преобразуем это уравнение



(10)
Это уравнение эллипса, оси которого по­вернуты относительно координатных осей х и у. Ори­ентация эллипса и его полуоси зависят довольно сложным образом от амплитуд Aи В и разности фаз α.
Попробуем найти форму траектории для нескольких частных случаев.

1. 
   Разность фаз α равна нулю.
   

В этом случае уравнение (10) упрощается следующим образом:

(11)

Отсюда получается уравнение прямой:



Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой ω и ам­плитудой, равной (рис. 5а).

2. 
   Разность фаз α равна ±π.
   

Уравнение (10) имеет вид

(12)

Следовательно, результирующее движение представ­ляет собой гармоническое колебание вдоль прямой

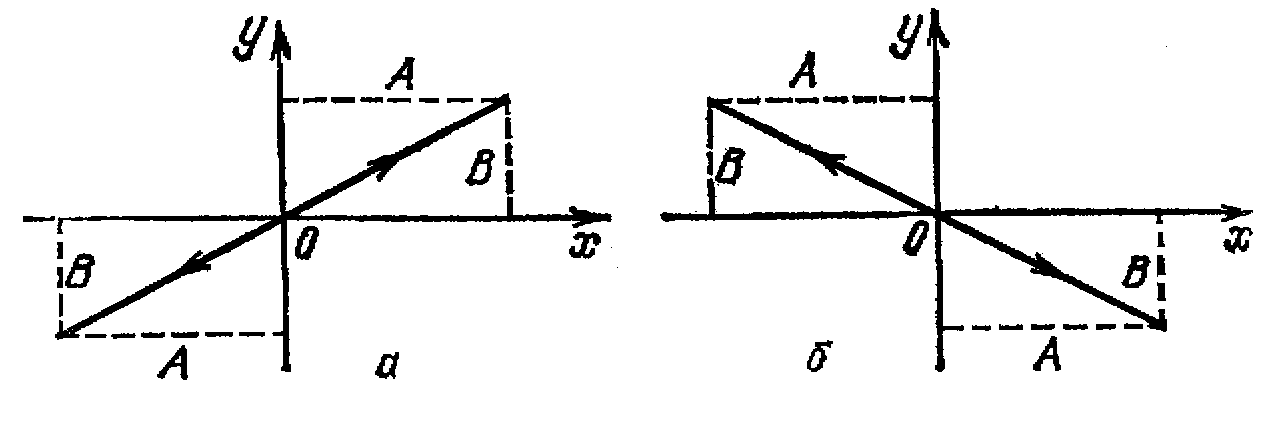
(рис. 5б)



Рис.5.

3. 
   Разность фаз .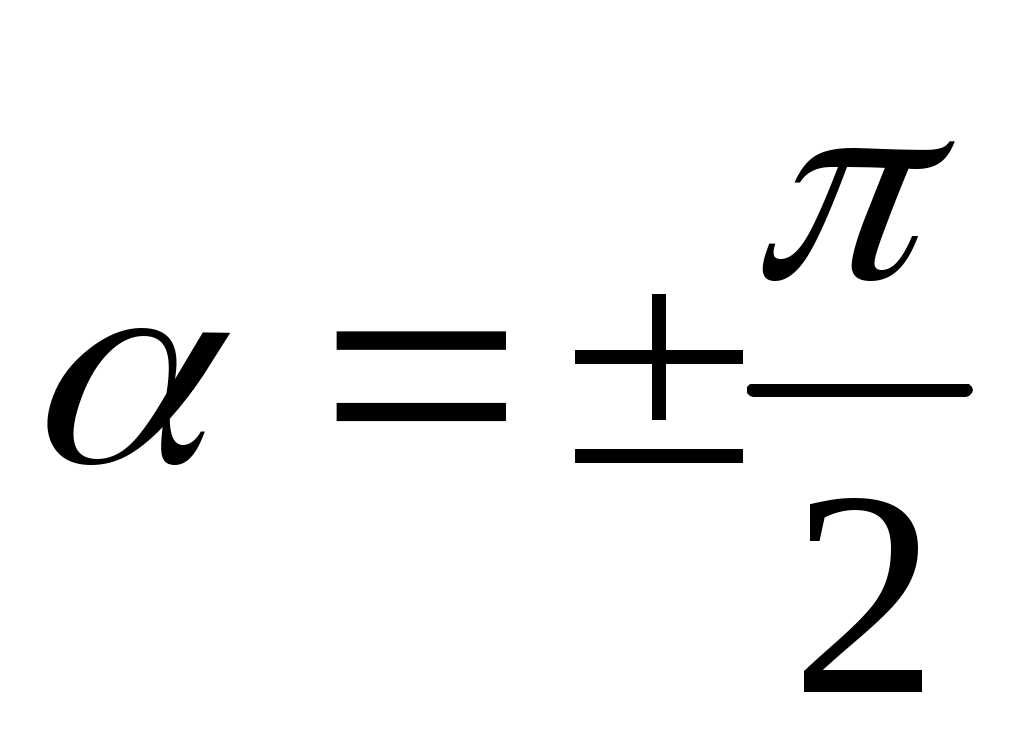
   

Уравнение (10) переходит в уравнение эллипса, приведенного к координатным осям:

(13)



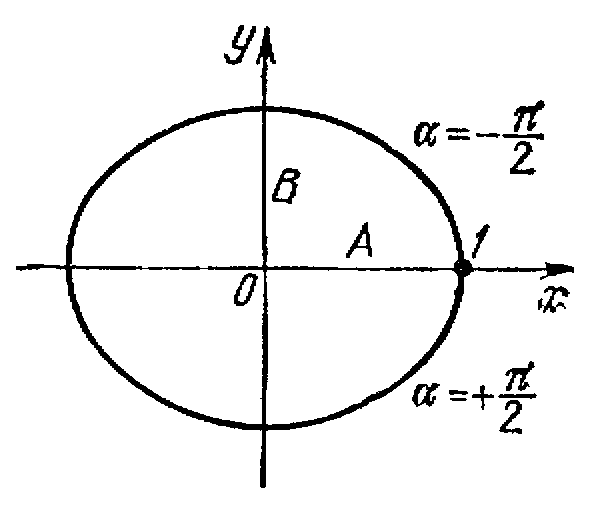
Рис.6.
Полуоси эллипса равны соответствующим амплиту­дам колебаний. При равенстве амплитуд А и В эллипс превращается в окружность.

Случаи и отличаются на­правлением движения по эллипсу или окружности.

Следовательно, равномерное движение по окружности радиуса R с угловой скоростью ω может быть представлено как сумма двух взаимно перпен­дикулярных колебаний:

,

(знак плюс в выражении для у соответствует движе­нию против часовой стрелки, знак минус — движе­нию по часовой стрелке).
Если частоты взаимно перпендикулярных колеба­ний не одинаковы, то траектории результирующего движения имеют вид сложных кривых, на­зываемых фигурами Лиссажу.



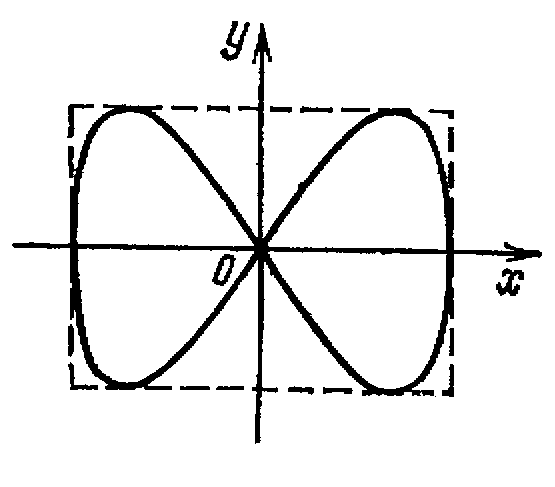
Рис.7. Фигура Лиссажу для

отношения ча­стот 1:2 и

разности фаз π/2



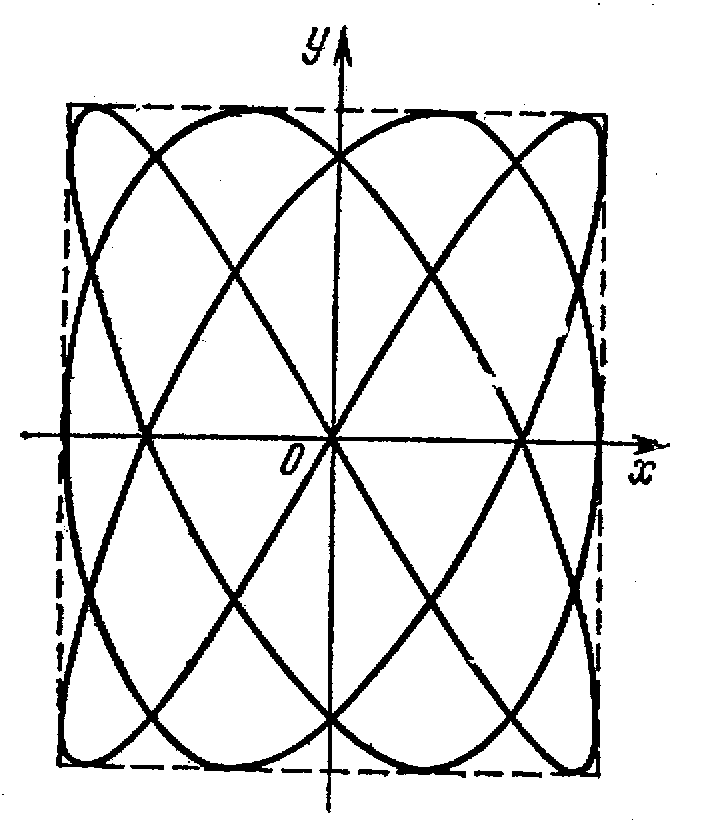
Рис.8. Фигура Лиссажу для отношения частот 3:4

и разности фаз π/2

Наблюдать биения и фигуры Лиссажу можно с помощью электронного осциллографа и звуковых генераторов.

---

Порядок выполнения задания.

1. Ознакомиться с инструкциями к осциллографу и звуковым генераторам, подобрать режим их работы.
Описание установки:
1)Схема установки (см. рис.9.) :

1. 
   Звуковой генератор( в нем совмещены два звуковых генератора, необходимых в данной работе)
   

U1-источник питания стабилизированный. Питает 1-й звуковой генератор (U1 = 5V)

U2- источник питания стабилизированный. Питает 2-й звуковой генератор (U1 = 15V)

1а и 1б – переключатели задаваемой частоты сигналов на выходе из генераторов;

2 – кнопка синхронизации колебаний;

3а и 3б – ручки регулирования амплитуды сигналов на выходе из генераторов

ЗГ.1 и ЗГ2 – выходы звукового генератора.

2.Осциллограф

4 – входное гнездо для подачи исследуемых сигналов;

5 – ручка управления усилителем Y ( V/дел – устанавливает коэффициент вертикального отклонения сигнала; плавно – обеспечивает плавную регулировку коэффициент отклонения в каждом положении переключателя V/дел)

6 – переключатель, который устанавливает вид развертки;

7 – входное гнездо для внешнего синхронизирующего сигнала. Это гнездо используется также для внешнего горизонтального входа, если переключатель 6 установлен в положение X.

8 – ручка управления разверткой (устанавливает скорость развертки)

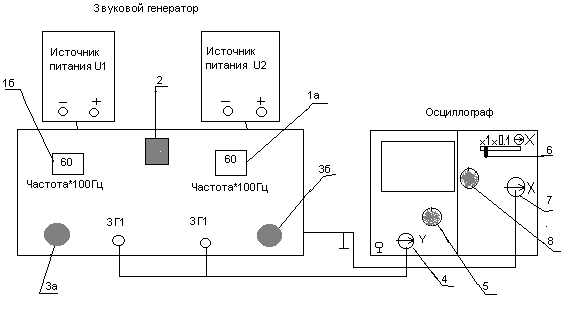
Рис. 9.

1.Изучить биения.

1.Соединить звуковой генератор с осциллографом как показано на рис.9 (переключатель 6 установить в крайнее левое положение). Условием для получения отчетливой осциллограммы биений является равенство амплитуд складываемых колебаний.

2. Получить задание у преподавателя по изучению биений.
2.Изучить сложение взаимно перпендикулярных колебаний.

1.Подать на вход Y осциллографа один звуковой сигнал. А на вход Х осциллографа второй сигнал от генератора. При этом переключатель 6 (рис.7) должен быть в крайнем правом положении. В этом положении отключается развертка.

2.Далее установить одинаковые амплитуды и получить на экране осциллографа кривые (фигуры Лиссажу), возникающие в результате сложения двух взаимно перпендикулярных колебаний. Отношение частот складываемых колебаний выбирать равными 1:1, 1:2, 2:3, 3:4. Зарисовать наблюдаемые фигуры (для фиксации фигур Лиссажу нажать кнопку синхронизации колебаний – 2(рис.9).

---