Файл: Лабораторная работа 1. Определение земного ускорения свободного падения при помощи оборот ного и математического маятников.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 196
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ВОПРОСЫ.
1. Что такое абсолютно черное тело и серое тело?
2. Нарисуйте спектр излучения абсолютно черного тела?
3. Как зависит от температуры спектр излучения абсолютно черного тела?
4. Изложить кратко сущность метода, использованного в данной работе для определения σ.
5. Пояснить понятие яркостной, цветовой и радиационной температуры.
6. Объяснить устройство и принцип действия пирометра.
7. Какую температуру измеряет пирометр, используемый в работе?
Литература.
-
Трофимова Т.И. Курс физики. М: Высшая школа. 1997 -
Ландсберг Г.С. Оптика. М.: Издательство»Наука». 1976
ЛАБОРАТОРНАЯ РАБОТА № 17.
ИЗУЧЕНИЕ ЯВЛЕНИЯ ИНТЕРФЕРЕНЦИИ СВЕТА.
ОПРЕДЕЛЕНИЕ РАДИУСА КРИВИЗНЫ ЛИНЗЫ И ДЛИНЫ СВЕТОВОЙ ВОЛНЫ С ПОМОЩЬЮ КОЛЕЦ НЬЮТОНА.
Вопросы теории. Свет, с точки зрения классической электродинамики, представляет собой поперечные электромагнитные волны, распространяющиеся в вакууме со скоростью с=3108 м/c. Волны одинаковой частоты с постоянной разностью фаз называются когерентными. В результате наложения когерентных волн наблюдается явление интерференции: усиление интенсивности света в одних местах и ослабление в других.
В действительности излучение света телами является результатом излучения отдельных атомов. В силу этого два любых источника не являются когерентными и не могут дать интерференционную картину. Для получения интерференционной картины необходимо излучение от одного источника разделить на два потока и заставить их встретиться после прохождения различных оптических путей. В случае такого разделения эти потоки можно трактовать как исходящие из двух совершенно одинаковых источников. Все элементарные акты излучения, происходящие в одном источнике
, одновременно повторяются в другом, но доходят до данной точки экрана с некоторым запаздыванием , определяемым разностью хода . Для получения интерференции важно, чтобы разность хода между интерферирующими лучами не была очень велика, так как они должны принадлежать к одному и тому же акту излучения.
Интерференция света при отражении от тонких пластинок или пленок.
При падении световой волны на тонкую прозрачную пластинку (или пленку) происходит отражение от обеих поверхностей пластинки. В результате возникают две световые волны, которые при известных условиях могут интерферировать.
Пусть в точку О (рис.1) на прозрачную пленку в виде клина с малым углом падает пучок света. Часть света (луч 1) отразится от верхней поверхности пленки, другая часть (луч 2), переломившись, отразится от нижней поверхности.


 2
2 1
1
 n1 i А
n1 i А
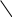
 i
i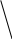

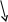 O В
O В 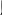
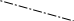
 n2 d r
n2 d r 


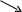
n3 С
Рис. 1.
Определим оптическую разность хода (т.е. разность оптических длин проходимых электромагнитными волнами путей) между двумя когерентными лучами 1 и 2 (см. рис. 1). Оптическая длина пути – это произведение геометрической длины пути S световой волны в данной среде на показатель n преломления этой среды.
= n2(ОС + СВ) – n1ОА (1)
Подставив значения ОА = 2d tg r sin i, ОС + СВ = 2d/cos r и
n2/n1 = sin i/sin r в ( 1) , получим
= 2d n2 cos r, (2)
где d –толщина пленки; n1 и n2 – показатели преломления окружающей среды и материала пленки соответственно; i – угол падения света на пленку; r – угол преломления.
При вычислении необходимо учесть и то обстоятельство, что при отражении световой волны от границ раздела сред, для которых n2 n1,
фаза световых колебаний претерпевает изменение на (это соответствует разности хода /2). Если показатель преломления пленки n2 n1, то происходит скачок фазы для луча 1; в случае n2 n1 изменяет свою фазу при отражении в точке С луч 2.
С учетом этого замечания соотношение (2) следует записать в виде
= 2d n2 cos r /2. (3)
Результат интерференции зависит от значения .
При = m получаются максимумы, при = (m + 1/2) - минимумы интенсивности (здесь m – целые числа). Значение m называется порядком интерференции. Максимальный порядок интерференции при заданных и d ограничен значением cos r = 1.
Если считать, что человеческий глаз распознает оттенки, отличающиеся на величину = 10 нм, то для наблюдения цветных интерференционных полос в тонких пленках, освещаемых белым светом, необходима толщина d 10 мкм. Такому условию удовлетворяют, например, мыльные пленки, пленки масел на поверхности воды.
Характер локализованной интерференционной картины (т.е. её расположение) задается двумя параметрами d и r, определяющими положение максимумов и минимумов интерференции. В связи с этим различают два случая, а именно: полосы равного наклона и полосы равной толщины.
При d = const (плоскопараллельный воздушный слой, тонкая плоскопараллельная стеклянная пластинка) интерферирующими являются параллельные между собой лучи (рис. 2). При этом оптическая разность хода зависит от угла преломления r (следовательно, и от угла падения i).



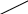
 экран
экран

 i В линза
i В линзаn
 =1 С
=1 С 


 О
О
 r r n d
r r n d  А
А Рис.2.
Геометрическим местом точек пересечения всех интерферирующих пар лучей, падающих от широкого источника на пластину под одним и тем же углом i и собранных линзой на экране, является окружность на экране с центром, соответствующим углу падения i = 0.
Если для какого-то значения r величина = m, то на экране будет светлое кольцо, если = (2m + 1)/2, то темное кольцо. Такие интерференционные полосы называются полосами равного наклона, они локализованы на экране ( в отсутствии линзы – в бесконечности).
При изменяющейся толщине пленки (тонкий стеклянный клин) для постоянного угла падения (параллельный пучок, для которого r = const) условия максимума и минимума зависят от толщины пленки d в том или ином ее месте (рис.1).
Полосы интерференции, удовлетворяющие условию максимума (или минимума) и соответствующие одной и той же толщине клина (пленки), в этом случае локализованы над или под поверхностью пленки и называются полосами равной толщины.
Так, для правильного клина интерференционная картина представляет собой чередование светлых и темных полос, параллельных ребру клина.
Локализация полос равной толщины зависит от угла падения i и угла клина . При фиксированном интерференционная картина расположена тем ближе к поверхности пленки, чем меньше угол падения i. В случае нормального падения лучей (i = 0) полосы равной толщины локализованы на поверхности пленки.
Для постоянного, но не равного нулю угла падения i интерференционная картина полос равной толщины расположена тем дальше от поверхности, чем меньше угол клина . При = 0 (плоскопараллельный слой) полосы равной толщины переходят в полосы равного наклона, локализованные в бесконечности.
ТЕОРИЯ МЕТОДА.
Классическим примером полос равной толщины являются кольца Ньютона,