Файл: Лабораторная работа 1. Определение земного ускорения свободного падения при помощи оборот ного и математического маятников.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 190
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3.Проверить правило
где
Контрольные вопросы:
1. Уравнение и график гармонических колебаний.
2. Что такое гармоническое колебание, его уравнение и график.
3. При каких условиях наблюдаются биения?
4. При каких условиях наблюдаются фигуры Лиссажу?
Литература:
-
Физический практикум/ Под ред. Г.С. Кембровского – Мн.: изд.-во «Университетское», 1986-352с. -
Сивухин Д.В. Общий курс физики .- М.: Наука, 1990 т1.Механика. -
Трофимова Т.И. Курс физики.-М: «Высшая школа», 1997.
Лабораторная работа №3
Определение коэффициента внутреннего трения жидкости
по методу Пуазейля.
Цель:определить вязкость воды методом Пуазейля.
Оборудование и принадлежности: установка для проведения измерений, мерный стакан, линейка, секундомер.
Схема установки.
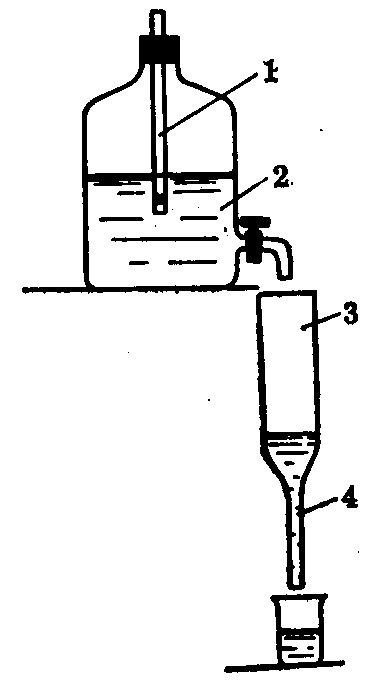
Рис. 1
ОПИСАНИЕ УСТАНОВКИ
Прибор состоит из широкой стеклянной трубки 3, заканчивающейся капилляром 4 (рис. 1). Исследуемая жидкость в трубку 3 поступает из сосуда Мариотта 2. Через пробку в верхней части сосуда 2 пропущена длинная стеклянная трубка 1. В трубку 3 жидкость поступает равномерно, что позволяет установить ее уровень в этой трубке постоянным.
ЭЛЕМЕНТЫ ТЕОРИИ.
Для жидкостей характерна достаточно плотная упаковка молекул (об этом свидетельствует их малая сжимаемость). Поэтому каждая молекула, постоянно сталкиваясь с соседними молекулами, в течение некоторого времени колеблется около определенного положения равновесия. Время от времени молекула, получив от соседней молекулы достаточную энергию, скачком переходит в новое положение равновесия. Дальность этого скачка примерно равна размеру молекул (10-10м). Среднее время , в течение которого молекула колеблется около данного положения равновесия
, называется временем оседлой жизни молекулы. Расчеты показывают, что
где 0 – средний период колебаний молекулы; E – минимальная энергия, которую нужно сообщить молекуле жидкости, чтобы она могла перейти из одного положения равновесия в другое (Е10-20 Дж); k – постоянная Больцмана; Т – абсолютная температура жидкости. Для воды при комнатной температуре 0 10-13с, а 10-11с. С повышением температуры подвижность молекул возрастает, время оседлой жизни уменьшается.
При движении жидкости (или газа) между слоями, перемещающимися с различной скоростью, возникают силы внутреннего трения (вязкости). Эти силы направлены так, что ускоряют медленно движущиеся слои или замедляют быстро движущиеся.
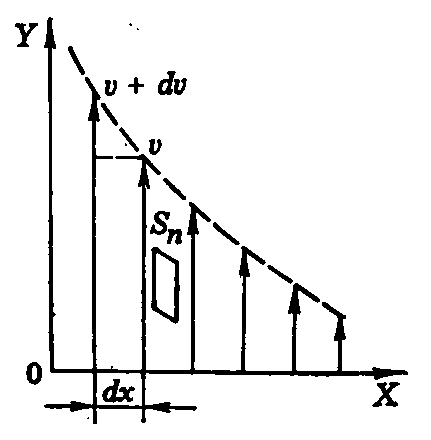
Рис. 2
Рассмотрим ламинарный поток жидкости в направлении оси Y (рис. 2). Слои жидкости движутся с разными скоростями. Скорости двух слоев, отстоящих друг от друга на расстоянии dx, отличаются на d. Величина
Ньютон установил, что модуль силы внутреннего трения между слоями прямо пропорционален площади их соприкосновения и модулю градиента скорости:
где – коэффициент пропорциональности, называемый вязкостью (или коэффициентом вязкости) жидкости; площадка Sn ориентирована перпендикулярно к градиенту скорости.
Между слоями жидкости будет происходить передача импульса. По второму закону Ньютона
где dp – величина импульса, переносимого за время
dt от слоя к слою через поверхность Sn, перпендикулярную к направлению переноса импульса. Знак минус указывает, что импульс переносится от слоев, движущихся с большей скоростью, к слоям, движущимся с меньшей скоростью (в нашем случае вдоль оси Х).
Импульс, переносимый через единичную площадку, расположенную перпендикулярно к переносимому потоку импульса за единицу времени, называется плотностью потока импульса
Соотношения (2)-(4) являются различными формами записи основного закона вязкости - закона Ньютона. Физический смысл коэффициента вязкости можно определить из любого соотношения. Например, из (4) следует, что вязкость определяется плотностью потока импульса при градиенте скорости , равном единице.
Вязкость жидкости зависит от ее химического состава, примесей и температуры. С повышением температуры Т вязкость жидкости уменьшается по закону
=АexpE/(kT). (5)
Здесь коэффициент А для каждой конкретной жидкости можно приблизительно считать постоянным.
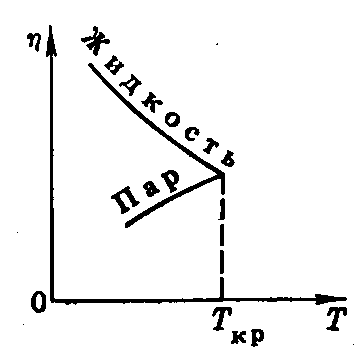
Рис. 3
Вязкость газов (паров) в отличие от жидкостей с повышением температуры медленно увеличивается (
, а силы притяжения уменьшаются и, как следствие, уменьшается вязкость.
Величина
/ (6)
называется кинематической вязкостью.
Приборы для измерения вязкости называются вискозиметрами. Существует несколько методов определения вязкости: метод Стокса, основанный на измерении скорости падения шарика в исследуемой жидкости; метод
Пуазейля, в основе которого лежит измерение объема жидкости (газа), протекающей через капиллярную трубку; метод затухающих колебаний тела, подвешенного на упругой нити в исследуемой среде, и другие.
Теория метода. Вязкость жидкости может быть определена по объему жидкости, протекающей через капиллярную трубку (метод Пуазейля). Этот метод применим только к случаю ламинарного течения жидкости (газа).
Пусть на концах вертикальной капиллярной трубки длиной l и радиусом Rсоздана постоянная разность давлений p. Выделим внутри капилляра цилиндрический столбик жидкости радиусом r и высотой h. На боковую поверхность этого столбика действует сила внутреннего трения
Если p1 иp2 - давление на верхнее и нижнее сечения соответственно, то силы давления
Сила тяжести
где – плотность жидкости.
При установившемся движении
Отсюда
где (p1-p2)/h - изменение давления, приходящееся на единицу длины капилляра. Это постоянная вдоль всего капилляра величина. Поэтому
(p1 - p2)/h = p/l. (12)
После интегрирования (11) с учетом (12) получим
При r = R скорость = 0, следовательно, постоянная интегрирования
(14)
Объем жидкости, протекающей через некоторое сечение трубки в пространстве между цилиндрическими поверхностями радиусами r и r + dr за
время t, определяется по формуле dV = 2rdrt или
Полный объем жидкости, протекающей через сечение капилляра за время t:
Если разность давлений на концах капилляра создается столбом жидкости высотой H, то p = gH. Тогда
Порядок выполнения задания.
1. Подставить под капилляр стакан, открыть кран в сосуде Мариотта и ожидать, пока уровень жидкости в широкой трубке установится постоянным.
2. Определить время t истечения через капилляр определенного объема жидкости V. Объем жидкости определяют с помощью мерного стакана.
3. Измерить высоту столба жидкости H в широкой трубке и длину капилляра l.
4. По формуле (17) рассчитать вязкость жидкости.
5. Провести ряд повторных наблюдений величин H, l, t, V.
6. По формуле (17) определить <>.
Результаты измерений и вычислений занести в таблицу 1.
Таблица 1.

7. Сравнить полученный результат с табличными данными .
На основании проделанных измерений сформулировать цель работы и сделать выводы.
Контрольные вопросы.
-
Какой физический смысл коэффициента внутреннего трения? -
Какая физическая природа сил внутреннего трения в жидкости?
3. Выведите формулу для определения вязкости жидкости по методу Пуазейля.
4. Каков профиль скоростей течения жидкости в капиллярной трубке?
5. Какое течение жидкости называется ламинарным и турбулентным.
ЛИТЕРАТУРА
1. Трофимова Т.И. Курс физики. -М.: Высшая школа, 1997.
2. Матвеев А.Н. Молекулярная физика. -М.: Высшая школа, 1987,360 с.
3. Савельев И.В. Курс общей физики. -М.: Наука, 1982. Т. 1. Механика. Молекулярная физика. -432 с.
-
Физический практикум. Под ред. Кембровского Г.С. -Минск: Изд-во "Университетское", 1986. -352 с.
Лабораторная работа №3