БЕЛГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. В.Г. ШУХОВА

КАФЕДРА (Высшей математики)

Контрольная работа № 1

По дисциплине: Математика


Выполнил: Вашукевич Илья Александрович

студент 1 курса групп Мд-11
Института дистанционного образования

Проверил:

Белгород, 2018 г.

1Контрольная работа № 1

1 курс, 1 семестр

1. 
   Решить систему линейных уравнений тремя методами: методом Крамера, методом обратной матрицы, методом Гаусса:
   

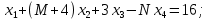
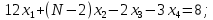
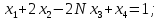
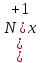
Решение методом Крамера
Запишем систему в виде:
B^T = (16,8,1,8)

Система совместна тогда и только тогда, когда системный (главный) определитель не равен нулю.

Найдем определитель:

Минор для (1,1):
Найдем определитель для этого минора.

∆_1,1 = (-1)*((-2)*8-1*1)-2*((-2)*8-1*(-3))+(-3)*((-2)*1-(-2)*(-3)) = 67

Минор для (2,1):
Найдем определитель для этого минора.

∆_2,1 = 12*((-2)*8-1*1)-2*(3*8-1*(-1))+(-3)*(3*1-(-2)*(-1)) = -257

Минор для (3,1):
Найдем определитель для этого минора.

∆_3,1 = 12*((-2)*8-1*(-3))-(-1)*(3*8-1*(-1))+(-3)*(3*(-3)-(-2)*(-1)) = -98

Минор для (4,1):
Найдем определитель для этого минора.

∆_4,1 = 12*((-2)*1-(-2)*(-3))-(-1)*(3*1-(-2)*(-1))+2*(3*(-3)-(-2)*(-1)) = -117

Определитель:

∆ = (-1)¹⁺¹1*67+(-1)²⁺¹12*(-257)+(-1)³⁺¹1*(-98)+(-1)⁴⁺¹2*(-117) = 1*67-12*(-257)+1*(-98)-2*(-117) = 3287

Заменим 1-ый столбец матрицы А на вектор результата В.

16	12	3	-1
8	-1	-2	-3
1	2	-2	1
8	-3	1	8

---

Найдем определитель полученной матрицы.
Минор для (1,1):
Найдем определитель для этого минора.

∆_1,1 = (-1)*((-2)*8-1*1)-2*((-2)*8-1*(-3))+(-3)*((-2)*1-(-2)*(-3)) = 67

Минор для (2,1):
Найдем определитель для этого минора.

∆_2,1 = 12*((-2)*8-1*1)-2*(3*8-1*(-1))+(-3)*(3*1-(-2)*(-1)) = -257

Минор для (3,1):
Найдем определитель для этого минора.

∆_3,1 = 12*((-2)*8-1*(-3))-(-1)*(3*8-1*(-1))+(-3)*(3*(-3)-(-2)*(-1)) = -98

Минор для (4,1):
Найдем определитель для этого минора.

∆_4,1 = 12*((-2)*1-(-2)*(-3))-(-1)*(3*1-(-2)*(-1))+2*(3*(-3)-(-2)*(-1)) = -117

Определитель минора:

∆₁ = (-1)^{1 + 1}a₁₁∆₁₁ + (-1)^{2 + 1}a₂₁∆₂₁ + (-1)^{3 + 1}a₃₁∆₃₁ + (-1)^{4 + 1}a₄₁∆₄₁ = (-1)¹⁺¹16*67+(-1)²⁺¹8*(-257)+(-1)³⁺¹1*(-98)+(-1)⁴⁺¹8*(-117) = 16*67-8*(-257)+1*(-98)-8*(-117)
Заменим 2-ый столбец матрицы А на вектор результата В.

1	16	3	-1
12	8	-2	-3
1	1	-2	1
2	8	1	8

Найдем определитель полученной матрицы.
Минор для (1,1):
Найдем определитель для этого минора.

∆_1,1 = 8*((-2)*8-1*1)-1*((-2)*8-1*(-3))+8*((-2)*1-(-2)*(-3)) = -187

Минор для (2,1):
Найдем определитель для этого минора.

∆_2,1 = 16*((-2)*8-1*1)-1*(3*8-1*(-1))+8*(3*1-(-2)*(-1)) = -289

Минор для (3,1):
Найдем определитель для этого минора.

∆_3,1 = 16*((-2)*8-1*(-3))-8*(3*8-1*(-1))+8*(3*(-3)-(-2)*(-1)) = -496

Минор для (4,1):
Найдем определитель для этого минора.

∆_4,1 = 16*((-2)*1-(-2)*(-3))-8*(3*1-(-2)*(-1))+1*(3*(-3)-(-2)*(-1)) = -147

Определитель минора:

∆₂ = (-1)^{1 + 1}a₁₁∆₁₁ + (-1)^{2 + 1}a₂₁∆₂₁ + (-1)^{3 + 1}a₃₁∆₃₁ + (-1)^{4 + 1}a₄₁∆₄₁ = (-1)¹⁺¹1*(-187)+(-1)²⁺¹12*(-289)+(-1)³⁺¹1*(-496)+(-1)⁴⁺¹2*(-147) = 1*(-187)-12*(-289)+1*(-496)-2*(-147)
Заменим 3-ый столбец матрицы А на вектор результата В.

1	12	16	-1
12	-1	8	-3
1	2	1	1
2	-3	8	8

---

Найдем определитель полученной матрицы.
Минор для (1,1):
Найдем определитель для этого минора.

∆_1,1 = (-1)*(1*8-8*1)-2*(8*8-8*(-3))+(-3)*(8*1-1*(-3)) = -209

Минор для (2,1):
Найдем определитель для этого минора.

∆_2,1 = 12*(1*8-8*1)-2*(16*8-8*(-1))+(-3)*(16*1-1*(-1)) = -323

Минор для (3,1):
Найдем определитель для этого минора.

∆_3,1 = 12*(8*8-8*(-3))-(-1)*(16*8-8*(-1))+(-3)*(16*(-3)-8*(-1)) = 1312

Минор для (4,1):
Найдем определитель для этого минора.

∆_4,1 = 12*(8*1-1*(-3))-(-1)*(16*1-1*(-1))+2*(16*(-3)-8*(-1)) = 69

Определитель минора:

∆₃ = (-1)^{1 + 1}a₁₁∆₁₁ + (-1)^{2 + 1}a₂₁∆₂₁ + (-1)^{3 + 1}a₃₁∆₃₁ + (-1)^{4 + 1}a₄₁∆₄₁ = (-1)¹⁺¹1*(-209)+(-1)²⁺¹12*(-323)+(-1)³⁺¹1*1312+(-1)⁴⁺¹2*69 = 1*(-209)-12*(-323)+1*1312-2*69
Заменим 4-ый столбец матрицы А на вектор результата В.

1	12	3	16
12	-1	-2	8
1	2	-2	1
2	-3	1	8

Найдем определитель полученной матрицы.
Минор для (1,1):
Найдем определитель для этого минора.

∆_1,1 = (-1)*((-2)*8-1*1)-2*((-2)*8-1*8)+(-3)*((-2)*1-(-2)*8) = 23

Минор для (2,1):
Найдем определитель для этого минора.

∆_2,1 = 12*((-2)*8-1*1)-2*(3*8-1*16)+(-3)*(3*1-(-2)*16) = -325

Минор для (3,1):
Найдем определитель для этого минора.

∆_3,1 = 12*((-2)*8-1*8)-(-1)*(3*8-1*16)+(-3)*(3*8-(-2)*16) = -448

Минор для (4,1):
Найдем определитель для этого минора.

∆_4,1 = 12*((-2)*1-(-2)*8)-(-1)*(3*1-(-2)*16)+2*(3*8-(-2)*16) = 315

Определитель минора:

∆₄ = (-1)^{1 + 1}a₁₁∆₁₁ + (-1)^{2 + 1}a₂₁∆₂₁ + (-1)^{3 + 1}a₃₁∆₃₁ + (-1)^{4 + 1}a₄₁∆₄₁ = (-1)¹⁺¹1*23+(-1)²⁺¹12*(-325)+(-1)³⁺¹1*(-448)+(-1)⁴⁺¹2*315 = 1*23-12*(-325)+1*(-448)-2*315
Выпишем отдельно найденные переменные Х
Решение СЛАУ методом Гаусса.

Запишем систему в виде расширенной матрицы:
Умножим 1-ую строку на (12). Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:
Умножим 3-ую строку на (-12). Добавим 3-ую строку к 2-ой:
Умножим 3-ую строку на (2). Умножим 4-ую строку на (-1). Добавим 4-ую строку к 3-ой:
Умножим 1-ую строку на (25). Умножим 2-ую строку на (145). Добавим 2-ую строку к 1-ой:
Умножим 2-ую строку на (7). Умножим 3-ую строку на (25). Добавим 3-ую строку к 2-ой:

---

Умножим 1-ую строку на (29). Умножим 2-ую строку на (-4140). Добавим 2-ую строку к 1-ой:
Теперь исходную систему можно записать так:

x₄ = 853500/986100

x₃ = [-178 - ( - 255x₄)]/29

x₂ = [-6 - ( - 5x₃ - 6x₄)]/7

x₁ = [8 - ( - 3x₂ + x₃ + 8x₄)]/2

Из 1-ой строки выражаем x₄
Из 2-ой строки выражаем x₃
Из 3-ой строки выражаем x₂
Из 4-ой строки выражаем x₁


Решение СЛАУ методом обратной матрицы
Обозначим через А — матрицу коэффициентов при неизвестных; X — матрицу-столбец неизвестных; B - матрицу-столбец свободных членов:
Вектор B:

B^T=(16,8,1,8)

С учетом этих обозначений данная система уравнений принимает следующую матричную форму: А*Х = B.

Если матрица А — невырожденная (ее определитель отличен от нуля, то она имеет обратную матрицу А^-1. Умножив обе части уравнения на А^-1, получим: А^-1*А*Х = А^-1*B, А^-1*А=Е.

Это равенство называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А^-1.

Система будет иметь решение, если определитель матрицы A отличен от нуля.

Найдем главный определитель.

Минор для (1,1):
=-1•(-2•8-1•1)-2•(-2•8-1•(-3))+(-3•(-2•1-(-2•(-3))))=67

Минор для (2,1):
=12•(-2•8-1•1)-2•(3•8-1•(-1))+(-3•(3•1-(-2•(-1))))=-257

Минор для (3,1):
=12•(-2•8-1•(-3))-(-1•(3•8-1•(-1)))+(-3•(3•(-3)-(-2•(-1))))=-98

Минор для (4,1):
=12•(-2•1-(-2•(-3)))-(-1•(3•1-(-2•(-1))))+2•(3•(-3)-(-2•(-1)))=-117

Определитель:

∆=1•67-12•(-257)+1•(-98)-2•(-117)=3287

Итак, определитель 3287 ≠ 0, поэтому продолжаем решение. Для этого найдем обратную матрицу через алгебраические дополнения.

Пусть имеем невырожденную матрицу А:

=

Тогда:

=

где A_ij — алгебраическое дополнение элемента a_ij в определителе матрицы А, которое является произведением (—1)^i+j на минор (определитель) n-1 порядка, полученный вычеркиванием i-й строки и j-го столбца в определителе матрицы А.

Транспонированная матрица к матрице A имеет вид:
Вычисляем алгебраические дополнения.
∆_1,1=-1•(-2•8-1•1)-(-2•(2•8-1•(-3)))+(-3•(2•1-(-2•(-3))))=67

---

∆_1,2=-12•(-2•8-1•1)-3•(2•8-1•(-3))+(-1•(2•1-(-2•(-3))))=257
∆_1,3=12•(-2•8-(-3•1))-3•(-1•8-(-3•(-3)))+(-1•(-1•1-(-2•(-3))))=-98
∆_1,4=-12•(-2•1-(-3•(-2)))-3•(-1•1-(-3•2))+(-1•(-1•(-2)-(-2•2)))=117
∆_2,1=-12•(-2•8-1•1)-(-2•(1•8-1•2))+(-3•(1•1-(-2•2)))=207
∆_2,2=1•(-2•8-1•1)-3•(1•8-1•2)+(-1•(1•1-(-2•2)))=-40
∆_2,3=-1•(-2•8-(-3•1))-3•(12•8-(-3•2))+(-1•(12•1-(-2•2)))=335
∆_2,4=1•(-2•1-(-3•(-2)))-3•(12•1-(-3•1))+(-1•(12•(-2)-(-2•1)))=-31
∆_3,1=12•(2•8-1•(-3))-(-1•(1•8-1•2))+(-3•(1•(-3)-2•2))=255
∆_3,2=-1•(2•8-1•(-3))-12•(1•8-1•2)+(-1•(1•(-3)-2•2))=46
∆_3,3=1•(-1•8-(-3•(-3)))-12•(12•8-(-3•2))+(-1•(12•(-3)-(-1•2)))=-1207
∆_3,4=-1•(-1•1-(-3•2))-12•(12•1-(-3•1))+(-1•(12•2-(-1•1)))=200
∆_4,1=-12•(2•1-(-2•(-3)))-(-1•(1•1-(-2•2)))+(-2•(1•(-3)-2•2))=29
∆_4,2=1•(2•1-(-2•(-3)))-12•(1•1-(-2•2))+3•(1•(-3)-2•2)=-85
∆_4,3=-1•(-1•1-(-2•(-3)))-12•(12•1-(-2•2))+3•(12•(-3)-(-1•2))=301
∆_4,4=1•(-1•(-2)-(-2•2))-12•(12•(-2)-(-2•1))+3•(12•2-(-1•1))=345

Из полученных алгебраических дополнений составим присоединенную матрицу C:
Вычислим обратную матрицу:
Вектор результатов X

X=A^-1 • B
x
=
X^T=(1.21,0.94,1.47,0.87)

x₁=³⁹⁶⁶ / ₃₂₈₇=1.21

x₂=³⁰⁷⁹ / ₃₂₈₇=0.94

x₃=⁴⁸⁴¹ / ₃₂₈₇=1.47

x₄=²⁸⁴⁵ / ₃₂₈₇=0.87

2. 
   Заданы четыре точки в пространстве: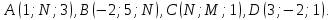
   

Найти:

1) длины векторов ;

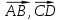2) координаты векторов ;

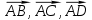3) проверить компланарность векторов ;

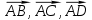4) уравнения прямых ;

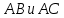5) уравнение плоскости

6) расстояние от точки до плоскости ;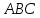

7) угол между векторами ;

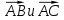8) уравнение медианы, проведенной из точки 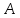на сторону 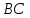треугольника ;

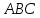9) уравнение перпендикуляра, опущенного на сторону

---

Смотрите также файлы

• Занятие Задания 1 5 просмотр попытки httpssdo icollege rumodquizreview phpattempt2414472&cmid33424 16.pdf

• Выполнение практических заданий по дисциплине государственная поддержка малого бизнеса.docx

• Исследование пищевых продуктов.pdf

• Сценарий выпускного вечера2018 11 класса маоу сош 6.docx

• Законодательная защита прав потребителей. Основные понятия, применяемые в Законе рф О защите прав потребителей.docx