Файл: Контрольная работа 1 По дисциплине Математика Выполнил Вашукевич Илья Александрович.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 68
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
из точки 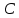 треугольника
треугольника  ;
;
10) площадь треугольника ;
;
11) координаты точки пересечения медиан треугольника ;
;
12) объем пирамиды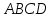 и ее высоту, опущенную на основание треугольника
и ее высоту, опущенную на основание треугольника  .
.
Даны координаты пирамиды: A(1,1,3), B(-2,5,1), C(1,8,1), D(3,-2,1)
2) Координаты векторов.
Координаты векторов находим по формуле:
X = xj - xi; Y = yj - yi; Z = zj - zi
здесь X,Y,Z координаты вектора; xi, yi, zi - координаты точки Аi; xj, yj, zj- координаты точки Аj;
Например, для вектора AB
X = x2 - x1; Y = y2 - y1; Z = z2 - z1
X = -2-1; Y = 5-1; Z = 1-3
AB(-3;4;-2)
AC(0;7;-2)
AD(2;-3;-2)
BC(3;3;0)
BD(5;-7;0)
CD(2;-10;0)
1) Модули векторов (длина ребер пирамиды)
Длина вектора a(X;Y;Z) выражается через его координаты формулой:
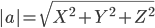
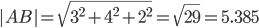
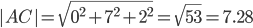
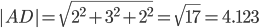
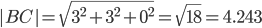
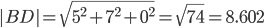
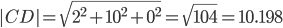
4) Уравнение прямых
Прямая, проходящая через точки A1(x1; y1; z1) и A2(x2; y2; z2), представляется уравнениями:
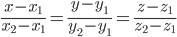
Параметрическое уравнение прямой:
x=x0+lt
y=y0+mt
z=z0+nt
Уравнение прямой AB(-3,4,-2)
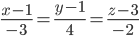
Параметрическое уравнение прямой:
x=1-3t
y=1+4t
z=3-2t
Уравнение прямой AC(0,7,-2)
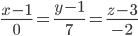
Параметрическое уравнение прямой:
x=1+0t
y=1+7t
z=3-2t
Уравнение прямой AD(2,-3,-2)
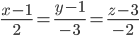
Параметрическое уравнение прямой:
x=1+2t
y=1-3t
z=3-2t
Уравнение прямой BC(3,3,0)
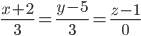
Параметрическое уравнение прямой:
x=-2+3t
y=5+3t
z=1+0t
5) Уравнение плоскости.
Если точки A1(x1; y1; z1), A2(x2; y2; z2), A3(x3; y3; z3) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:
Уравнение плоскости ABC
(x-1)(4(-2)-7(-2)) - (y-1)((-3)*(-2)-0(-2)) + (z-3)((-3)*7-0*4) = 6x - 6y - 21z + 63 = 0
Упростим выражение: 2x - 2y - 7z + 21 = 0
6) Длина высоты пирамиды, проведенной из вершины D(3,-2,1)
Расстояние d от точки M1(x1;y1;z1) до плоскости Ax + By + Cz + D = 0 равно абсолютному значению величины:
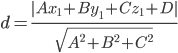
Уравнение плоскости ABC: 2x - 2y - 7z + 21 = 0
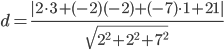
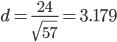
7) Угол между ребрами векторами AB и AC
Угол между векторами a1(X1;Y1;Z1), a2(X2;Y2;Z2) можно найти по формуле:
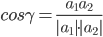
где a1a2 = X1X2 + Y1Y2 + Z1Z2
Найдем угол между ребрами AB(-3;4;-2) и AC(0;7;-2):
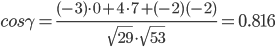
γ = arccos(0.816) = 35.2920
10) Площадь АВС
Площадь грани можно найти по формуле:
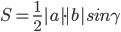
где
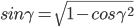
Найдем площадь грани ABC
Найдем угол между ребрами AB(-3;4;-2) и AC(0;7;-2):
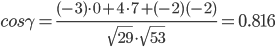
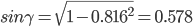
Площадь грани ABC
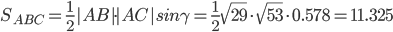
Найдем площадь грани с учётом геометрического смысла векторного произведения:
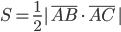
Векторное произведение:
=i(4(-2)-7(-2)) - j((-3)*(-2)-0(-2)) + k((-3)*7-0*4) = 6i - 6j - 21k
9) Уравнение плоскости, проходящей через точку перпендикулярно вектору AB
Уравнение плоскости, проходящей через точку M0(x0, y0, z0) перпендикулярно вектору N = (l,m,n), имеет вид:
l(x- x0) + m(y- y0) + n(z- z0) = 0
Координаты точки C(1;8;1)
Координаты вектора AB(-3;4;-2)
-3(x - 1) + 4(y - 8) + (-2)(z - 1) = 0
Искомое уравнение плоскости:
-3x + 4y - 2z-27 = 0
12) Уравнение высоты пирамиды через вершину D(3,-2,1)
Прямая, проходящая через точку M0(x0;y0;z0) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями:
Уравнение плоскости ABC: 2x - 2y - 7z + 21 = 0
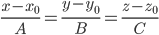
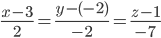
Объем пирамиды.
Объем пирамиды, построенный на векторах a1(X1;Y1;Z1), a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен:
Находим определитель матрицы
∆ = (-3)*(7*(-2)-(-3)*(-2))-0*(4*(-2)-(-3)*(-2))+2*(4*(-2)-7*(-2)) = 72
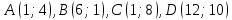
Уравнение прямой AB
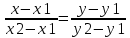
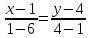
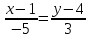
AB: 3x +5y - 23 = 0
Уравнение прямой AC
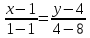
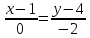
AC: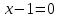
Уравнение прямой CD
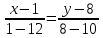
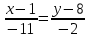
CD: -2х+11y -86 =0
Уравнение прямой BD
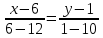
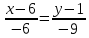
BD: -9х+6y +48=0
2) точка пересечения прямых решим систему уравнений
решим систему уравнений
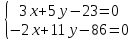
x = -16y - 109
-2(16y - 109) + 11y -86 = 0
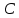 треугольника
треугольника  ;
; 10) площадь треугольника
 ;
; 11) координаты точки пересечения медиан треугольника
 ;
; 12) объем пирамиды
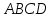 и ее высоту, опущенную на основание треугольника
и ее высоту, опущенную на основание треугольника  .
.Даны координаты пирамиды: A(1,1,3), B(-2,5,1), C(1,8,1), D(3,-2,1)
2) Координаты векторов.
Координаты векторов находим по формуле:
X = xj - xi; Y = yj - yi; Z = zj - zi
здесь X,Y,Z координаты вектора; xi, yi, zi - координаты точки Аi; xj, yj, zj- координаты точки Аj;
Например, для вектора AB
X = x2 - x1; Y = y2 - y1; Z = z2 - z1
X = -2-1; Y = 5-1; Z = 1-3
AB(-3;4;-2)
AC(0;7;-2)
AD(2;-3;-2)
BC(3;3;0)
BD(5;-7;0)
CD(2;-10;0)
1) Модули векторов (длина ребер пирамиды)
Длина вектора a(X;Y;Z) выражается через его координаты формулой:
4) Уравнение прямых
Прямая, проходящая через точки A1(x1; y1; z1) и A2(x2; y2; z2), представляется уравнениями:
Параметрическое уравнение прямой:
x=x0+lt
y=y0+mt
z=z0+nt
Уравнение прямой AB(-3,4,-2)
Параметрическое уравнение прямой:
x=1-3t
y=1+4t
z=3-2t
Уравнение прямой AC(0,7,-2)
Параметрическое уравнение прямой:
x=1+0t
y=1+7t
z=3-2t
Уравнение прямой AD(2,-3,-2)
Параметрическое уравнение прямой:
x=1+2t
y=1-3t
z=3-2t
Уравнение прямой BC(3,3,0)
Параметрическое уравнение прямой:
x=-2+3t
y=5+3t
z=1+0t
5) Уравнение плоскости.
Если точки A1(x1; y1; z1), A2(x2; y2; z2), A3(x3; y3; z3) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:
| = 0 |
Уравнение плоскости ABC
| = 0 |
(x-1)(4(-2)-7(-2)) - (y-1)((-3)*(-2)-0(-2)) + (z-3)((-3)*7-0*4) = 6x - 6y - 21z + 63 = 0
Упростим выражение: 2x - 2y - 7z + 21 = 0
6) Длина высоты пирамиды, проведенной из вершины D(3,-2,1)
Расстояние d от точки M1(x1;y1;z1) до плоскости Ax + By + Cz + D = 0 равно абсолютному значению величины:
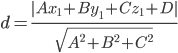
Уравнение плоскости ABC: 2x - 2y - 7z + 21 = 0
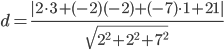
7) Угол между ребрами векторами AB и AC
Угол между векторами a1(X1;Y1;Z1), a2(X2;Y2;Z2) можно найти по формуле:
где a1a2 = X1X2 + Y1Y2 + Z1Z2
Найдем угол между ребрами AB(-3;4;-2) и AC(0;7;-2):
γ = arccos(0.816) = 35.2920
10) Площадь АВС
Площадь грани можно найти по формуле:
где
Найдем площадь грани ABC
Найдем угол между ребрами AB(-3;4;-2) и AC(0;7;-2):
Площадь грани ABC
Найдем площадь грани с учётом геометрического смысла векторного произведения:
Векторное произведение:
| = |
=i(4(-2)-7(-2)) - j((-3)*(-2)-0(-2)) + k((-3)*7-0*4) = 6i - 6j - 21k
9) Уравнение плоскости, проходящей через точку перпендикулярно вектору AB
Уравнение плоскости, проходящей через точку M0(x0, y0, z0) перпендикулярно вектору N = (l,m,n), имеет вид:
l(x- x0) + m(y- y0) + n(z- z0) = 0
Координаты точки C(1;8;1)
Координаты вектора AB(-3;4;-2)
-3(x - 1) + 4(y - 8) + (-2)(z - 1) = 0
Искомое уравнение плоскости:
-3x + 4y - 2z-27 = 0
12) Уравнение высоты пирамиды через вершину D(3,-2,1)
Прямая, проходящая через точку M0(x0;y0;z0) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями:
Уравнение плоскости ABC: 2x - 2y - 7z + 21 = 0
Объем пирамиды.
Объем пирамиды, построенный на векторах a1(X1;Y1;Z1), a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен:
| |
|
| |
| |
Находим определитель матрицы
∆ = (-3)*(7*(-2)-(-3)*(-2))-0*(4*(-2)-(-3)*(-2))+2*(4*(-2)-7*(-2)) = 72
-
Заданы четыре точки на плоскости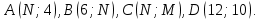
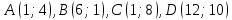
-
уравнения прямых ;
;
Уравнение прямой AB
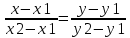
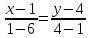
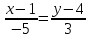
AB: 3x +5y - 23 = 0
Уравнение прямой AC
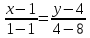
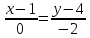
AC:
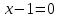
Уравнение прямой CD
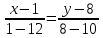
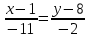
CD: -2х+11y -86 =0
Уравнение прямой BD
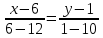
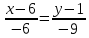
BD: -9х+6y +48=0
2) точка пересечения прямых
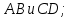 решим систему уравнений
решим систему уравнений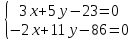
x = -16y - 109
-2(16y - 109) + 11y -86 = 0