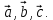Файл: Контрольная работа 1 По дисциплине Математика Выполнил Вашукевич Илья Александрович.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 67
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
y = (2*109 - 86)/ (32-11) = 132 /21 = 44/7
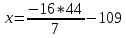= 595 / 7 = -85
Точка М1 (- 85; 44/7)
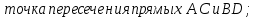решим систему уравнений
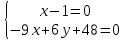
x =1
6y = 9-48
y = -13/2 = -6.5
Точка М2 ( 1; -6.5 )
3) уравнение прямой, проходящей через точки пересечения прямых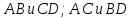
;
Уравнение прямой, проходящей через точки M1 M2
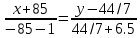
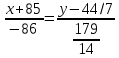
4) уравнения прямых, перпендикулярной прямой
и параллельной прямой 
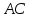, проходящих через точку 
;
Уравнение прямой, перпендикулярной AB и проходящей через точку D (12, 10)
AB, 3x +5y - 23 =
Искомая прямая перпендикулярна AB, значит очевидно, что нормальный вектор прямой AB будет направляющим искомой прямой:
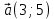
Тогда запишем уравнение искомой прямой:
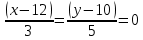
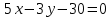
Уравнение прямой, параллельной AС и проходящей через точку D (12, 10)
AC:
Искомая прямая параллельна AС, значит очевидно, что нормальный вектор прямой AС будет нормальным вектором искомой прямой:
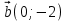
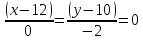
-2x+24 = 0
5) угол между прямыми ;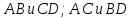
Косинус угла φ между двумя прямыми, заданными общими уравнениями
A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0, вычисляется по формуле:
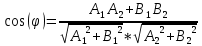
AB: 3x +5y - 23 = 0
CD: -2х+11y -86 =0
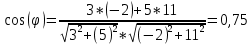
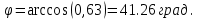
AС: x -1= 0
BD: -9х+6y +48=0
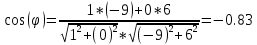
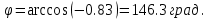
6) уравнение эллипса, проходящего через точки
;
Каноническое уравнение эллипса имеет вид:
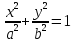
Если эллипс проходит через точки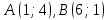
, необходимо решить систему уравнений:
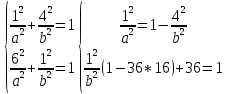
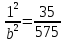
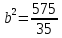
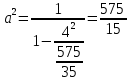
Получим уравнение эллипса
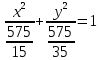
7) уравнение окружности с центром в точке
и радиусом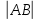 
;
;
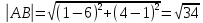Уравнение окружности с центром в точке (a, b) и радиусом R имеет вид:
(x — a)2 + (у — b)2 = R2
Запишем искомое уравнение:
(x — 1)2 + (у — 4)2 = 34
8) уравнение гиперболы, и начала координат, имеющей полуоси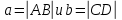
;
Общее каноническое уравнение гиперболы:
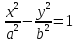
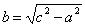
Уравнение гиперболы, симметричной относительно осей:
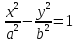
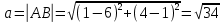
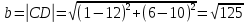
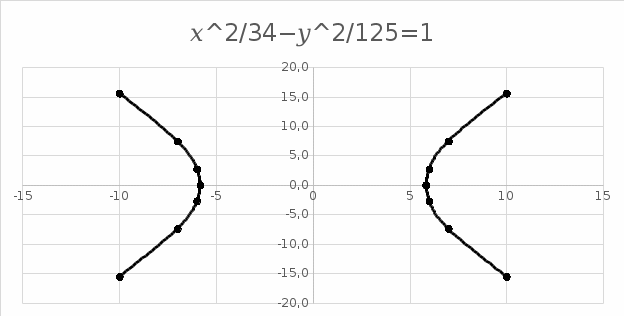Уравнение гиперболы:
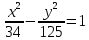
9) фокусное расстояние, эксцентриситет, уравнения асимптот и директрис полученной гиперболы;
фокусное расстояние
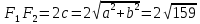
Эксцентриситет
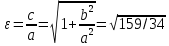
Уравнения асимптот
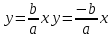
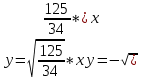
Уравнения директрис
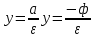
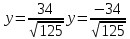
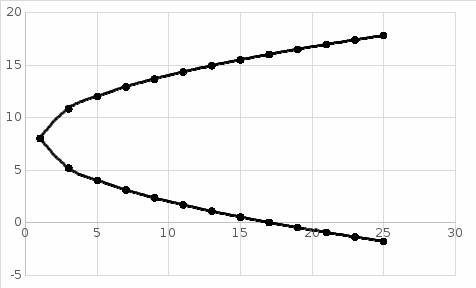
10) уравнение параболы, вершина которой находится в точке С, а фокус находится в точке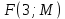
.
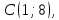
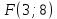
Каноническое уравнение параболы имеет вид
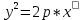
Уравнение параболы, с вtршиной в точке A (x0, y0)
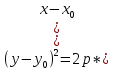
Фокальный параметр p, равен расстоянию от вершины до фокуса, следовательно:
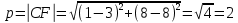
Запишем уравнение искомой параболы:
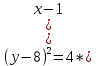
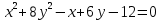
Приводим квадратичную форму
B = x2 + 8y2
к главным осям, то есть к каноническому виду. Матрица этой квадратичной формы:
Находим собственные числа и собственные векторы этой матрицы:
(1 - λ)x1 + 0y1 = 0
0x1 + (8 - λ)y1 = 0
Характеристическое уравнение:
λ2 -9 λ + 8 = 0
D=(-9)2 - 4*1*8=49
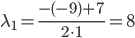
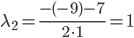
Исходное уравнение определяет эллипс (λ
1 > 0; λ2 > 0)
Вид квадратичной формы:
x2 + 8y2
Выделяем полные квадраты:
для x1:
(x12-21/2x1 + (1/2)2) -1(1/2)2 = (x1-1/2)2-1/4
для y1:
8(y12+23/8y1 + (3/8)2) -8(3/8)2 = 8(y1+3/8)2-9/8
В итоге получаем:
(x1-1/2)2+8(y1+3/8)2 = -85/8
Разделим все выражение на -85/8
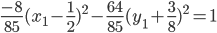
Полуоси эллипса:
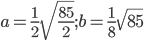
Данное уравнение определяет эллипс с центром в точке:
C(1/2; -3/8)
Найдем координаты фокусов F1(-c;0) и F2(c;0), где c - половина расстояния между фокусами
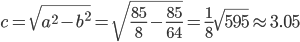
Итак, фокусы эллипса:
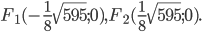
С учетом центра, координаты фокусов равны:
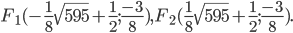
Тогда эксцентриситет будет равен:
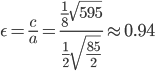
Вследствие неравенства c < a эксцентриситет эллипса меньше 1.
Ответ: кривая второго порядка - мнимый эллипс.
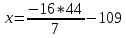= 595 / 7 = -85Точка М1 (- 85; 44/7)
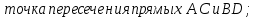решим систему уравнений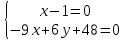 x =1
6y = 9-48
y = -13/2 = -6.5
Точка М2 ( 1; -6.5 )
3) уравнение прямой, проходящей через точки пересечения прямых
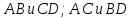; Уравнение прямой, проходящей через точки M1 M2
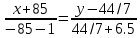
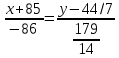
4) уравнения прямых, перпендикулярной прямой
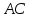и параллельной прямой , проходящих через точку ; Уравнение прямой, перпендикулярной AB и проходящей через точку D (12, 10)
AB, 3x +5y - 23 =
Искомая прямая перпендикулярна AB, значит очевидно, что нормальный вектор прямой AB будет направляющим искомой прямой:
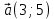
Тогда запишем уравнение искомой прямой:
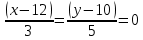
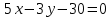
Уравнение прямой, параллельной AС и проходящей через точку D (12, 10)
AC:
Искомая прямая параллельна AС, значит очевидно, что нормальный вектор прямой AС будет нормальным вектором искомой прямой:
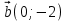
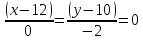
-2x+24 = 0
5) угол между прямыми
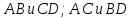; Косинус угла φ между двумя прямыми, заданными общими уравнениями
A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0, вычисляется по формуле:
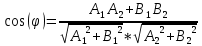
AB: 3x +5y - 23 = 0
CD: -2х+11y -86 =0
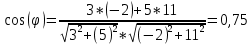
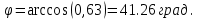
AС: x -1= 0
BD: -9х+6y +48=0
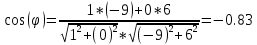
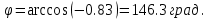
6) уравнение эллипса, проходящего через точки
; Каноническое уравнение эллипса имеет вид:
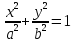
Если эллипс проходит через точки
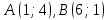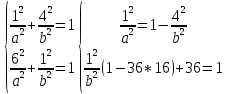
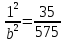
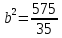
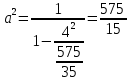
, необходимо решить систему уравнений: Получим уравнение эллипса
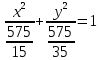
7) уравнение окружности с центром в точке
и радиусом 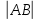; ;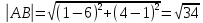Уравнение окружности с центром в точке (a, b) и радиусом R имеет вид:
(x — a)2 + (у — b)2 = R2
Запишем искомое уравнение:
(x — 1)2 + (у — 4)2 = 34
8) уравнение гиперболы, и начала координат, имеющей полуоси
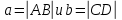;Общее каноническое уравнение гиперболы:
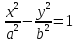
Уравнение гиперболы, симметричной относительно осей:
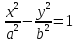
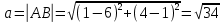
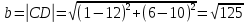
Уравнение гиперболы: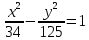 9) фокусное расстояние, эксцентриситет, уравнения асимптот и директрис полученной гиперболы;
фокусное расстояние
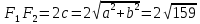
Эксцентриситет
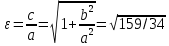
Уравнения асимптот
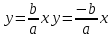
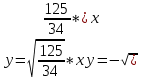
Уравнения директрис
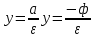
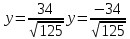
10) уравнение параболы, вершина которой находится в точке С, а фокус находится в точке
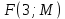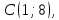
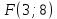
. Каноническое уравнение параболы имеет вид
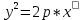
Уравнение параболы, с вtршиной в точке A (x0, y0)
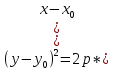
Фокальный параметр p, равен расстоянию от вершины до фокуса, следовательно:
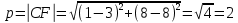
Запишем уравнение искомой параболы:
-
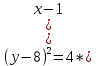
Определить вид кривой второго порядка 4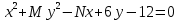
.
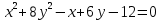
Приводим квадратичную форму
B = x2 + 8y2
к главным осям, то есть к каноническому виду. Матрица этой квадратичной формы:
| B = |
|
Находим собственные числа и собственные векторы этой матрицы:
(1 - λ)x1 + 0y1 = 0
0x1 + (8 - λ)y1 = 0
Характеристическое уравнение:
| = λ 2 - 9λ + 8 = 0 |
λ2 -9 λ + 8 = 0
D=(-9)2 - 4*1*8=49
Исходное уравнение определяет эллипс (λ
1 > 0; λ2 > 0)
Вид квадратичной формы:
x2 + 8y2
Выделяем полные квадраты:
для x1:
(x12-21/2x1 + (1/2)2) -1(1/2)2 = (x1-1/2)2-1/4
для y1:
8(y12+23/8y1 + (3/8)2) -8(3/8)2 = 8(y1+3/8)2-9/8
В итоге получаем:
(x1-1/2)2+8(y1+3/8)2 = -85/8
Разделим все выражение на -85/8
Полуоси эллипса:
Данное уравнение определяет эллипс с центром в точке:
C(1/2; -3/8)
Найдем координаты фокусов F1(-c;0) и F2(c;0), где c - половина расстояния между фокусами
Итак, фокусы эллипса:
С учетом центра, координаты фокусов равны:
Тогда эксцентриситет будет равен:
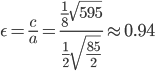
Вследствие неравенства c < a эксцентриситет эллипса меньше 1.
Ответ: кривая второго порядка - мнимый эллипс.
-
В базисе
заданы векторы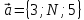 
, 
, 
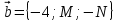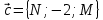и вектор 
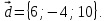Выразить вектор 
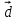в базисе векторов 