ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 45
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рис.5 – Расчет tож средствами Mathcad
Среднее число требований в очереди:
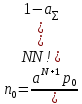
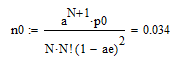
Рис.6. – Расчет n0 средствами Mathcad
Среднее число требований в системе:
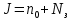
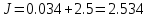
Среднее время нахождения заявки в системе:
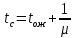
Рис.7 – Расчет tc средствами Mathcad
Сымитируем работу системы в среде GPSS:
NAK STORAGE 6
GENERATE (EXPONENTIAL(1,0,10))
QUEUE CONVEER
ENTER NAK
DEPART CONVEER
ADVANCE (EXPONENTIAL(1,0,25))
LEAVE NAK
TERMINATE 1
START 20000
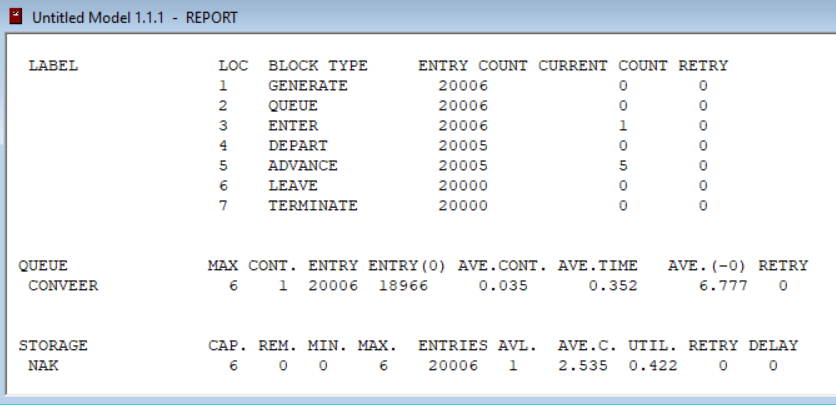
Рис.8. – Результаты моделирования СМО
Дополним программу так, чтобы выводились необходимые вероятности.
Вероятность простоя
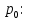
NAK STORAGE 6
GENERATE (EXPONENTIAL(1,0,10))
QUEUE CONVEER
ENTER NAK
DEPART CONVEER
ADVANCE (EXPONENTIAL(1,0,25))
LEAVE NAK
TERMINATE 1
START 20000
GENERATE 1
TEST G Q$CONVEER,1,APP1
SAVEVALUE PP0+,(1/20000)
APP1 TERMINATE 0
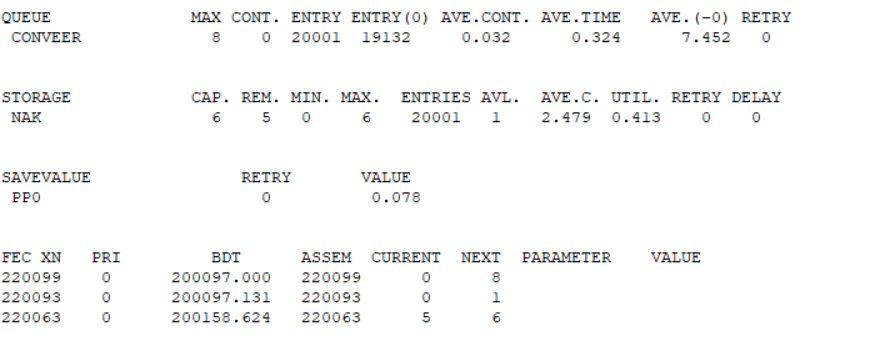
Рис.9. – Результаты моделирования СМО с вероятностью простоя
Остальные вероятности:
NAK STORAGE 6
GENERATE (EXPONENTIAL(1,0,10))
QUEUE CONVEER
ENTER NAK
DEPART CONVEER
ADVANCE (EXPONENTIAL(1,0,25))
LEAVE NAK
SAVEVALUE 1+,1
SAVEVALUE X1,Q$ CONVEER
TERMINATE 1
START 20000
GENERATE 1
TEST E Q$ CONVEER,0,M2
SAVEVALUE PP0+,(1/20000)
M2 TEST E Q$ CONVEER,1,M3
SAVEVALUE PP1+,(1/20000)
M3 TEST E Q$ CONVEER,2,M4
SAVEVALUE PP2+,(1/20000)
M4 TEST E Q$ CONVEER,3,M5
SAVEVALUE PP3+,(1/20000)
M5 TEST E Q$ CONVEER,4,M6
SAVEVALUE PP4+,(1/20000)
M6 TEST E Q$ CONVEER,5,M7
SAVEVALUE PP5+,(1/20000)
M7 TEST E Q$ CONVEER,6,M8
SAVEVALUE PP6+,(1/20000)
M8 TERMINATE
Сопоставим результаты, полученные теоретически и программно:
Таблица 1. – Анализ результатов
| | 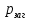 | 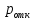 | 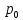 | 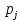 | 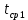 | 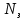 | 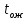 | 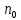 | 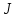 | 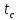 |
| Теор | 0.918 | 0 | 0.082 | p(1)=0.204 p(2)=0.255 p(3)=0.213 p(4)=0.133 p(5)=0.066 | 25 | 2.5 | 0.339 | 0.034 | 2.534 | 25.339 |
| GPSS | 0.923 | 0 | 0.078 | p(1)=0.195 p(2)=0.244 p(3)=0.203 p(4)=0.127 p(5)=0.063 | 25 | 2.535 | 0.352 | 0.035 | 2.57 | 25.12 |
На основе данных, полученных теоретическим и имитационным методами, можно сделать следующий вывод: результаты, полученные этими способами, отличаются незначительно. Аналитический метод считается более точным, чем имитационный. На практике и тот, и тот способы не вызывают сложности в расчетах при применении различных сред расчета/моделирования (Mathcad, GPSS).
СМО имеет большое значение вероятности загрузки системы, небольшое значение времени ожидания в очереди, среднее число занятых каналов обслуживания равно 2.5. Все это говорит о том, что СМО эффективна.
Улучшить данную СМО можно посредством замены рабочих на спецоборудование, которое будет изготавливать детали; уменьшить интервал поступления или увеличить его нельзя, потому что в первом случае увеличится время ожидания
, а во втором сократится производительность.
СМО с учетом дополнительных условий:
Сымитируем работу данной системы:
NAK STORAGE 5
fun1 FUNCTION C1,C4
6,25/7,25/8,23.5/9,22.5
GENERATE (EXPONENTIAL(1,0,10))
QUEUE CONVEER
ENTER NAK
DEPART CONVEER
ADVANCE (EXPONENTIAL(1,0,fn$fun1))
LEAVE NAK
SAVEVALUE 1+,1
SAVEVALUE X1,Q$ CONVEER
TERMINATE 1
START 20000
GENERATE 1
TEST E Q$ CONVEER,0,M2
SAVEVALUE PP0+,(1/20000)
M2 TEST E Q$ CONVEER,1,M3
SAVEVALUE PP1+,(1/20000)
M3 TEST E Q$ CONVEER,2,M4
SAVEVALUE PP2+,(1/20000)
M4 TEST E Q$ CONVEER,3,M5
SAVEVALUE PP3+,(1/20000)
M5 TEST E Q$ CONVEER,4,M6
SAVEVALUE PP4+,(1/20000)
M6 TEST E Q$ CONVEER,5,M7
SAVEVALUE PP5+,(1/20000)
M7 TEST E Q$ CONVEER,6,M8
SAVEVALUE PP6+,(1/20000)
M8 TERMINATE
Чтобы увидеть среднее время пребывания требования в системе введем дополнительную очередь TIME:
NAK STORAGE 5
fun1 FUNCTION C1,C4
6,25/7,25/8,23.5/9,22.5
GENERATE (EXPONENTIAL(1,0,10))
QUEUE TIME
QUEUE CONVEER
ENTER NAK
DEPART CONVEER
ADVANCE (EXPONENTIAL(1,0,fn$fun1))
LEAVE NAK
DEPART TIME
SAVEVALUE 1+,1
SAVEVALUE X1,Q$ CONVEER
TERMINATE 1
START 20000
GENERATE 1
TEST E Q$ CONVEER,0,M2
SAVEVALUE PP0+,(1/20000)
M2 TEST E Q$ CONVEER,1,M3
SAVEVALUE PP1+,(1/20000)
M3 TEST E Q$ CONVEER,2,M4
SAVEVALUE PP2+,(1/20000)
M4 TEST E Q$ CONVEER,3,M5
SAVEVALUE PP3+,(1/20000)
M5 TEST E Q$ CONVEER,4,M6
SAVEVALUE PP4+,(1/20000)
M6 TEST E Q$ CONVEER,5,M7
SAVEVALUE PP5+,(1/20000)
M7 TEST E Q$ CONVEER,6,M8
SAVEVALUE PP6+,(1/20000)
M8 TERMINATE
Таблица 2. – Результаты для задачи с учетом доп.условий
| Вероятность простоя системы | Среднее время ожидания в очереди | Среднее время пребывания требования в системе по результатам 5-ти прогонов моделей системы |
| 0.176 | 0.72 | 23.097 |
Сравним два варианта реализации системы по результатам 5-ти прогонов (I – исходный, II – с учетом дополнительных условий)
Таблица 3. – Сравнение двух вариантов реализации системы
| | I – исходный вариант системы | II – с учетом дополнительных условий |
| Вероятность простоя системы | 0.075 | 0.176 |
| Среднее время ожидания в очереди | 0.352 | 0.72 |
| Среднее время пребывания требования в системе | 25.12 | 23.097 |
Как видно из таблицы 3, дополнительные условия ускорили работу СМО, несмотря на уменьшение количества каналов, однако увеличилось время ожидания в очереди на обработку заявки.
Рассчитаем статистические характеристики (среднее, среднеквадратическое отклонение, минимальное и максимальное значения) показателя «время пребывания требования в системе» для двух вариантов реализации системы
Таблица 4. Сравнение статистических параметров времени пребывания задачи в системе
| | I – исходный вариант системы | II – с учетом дополнительных условий |
| Среднее | 25.12 | 23.097 |
| Дисперсия | 0.337 | 0.32 |
| СКО | 0.58 | 0.564 |
| Минимальное | 23.838 | 21.702 |
| Максимальное | 25.521 | 23.298 |
Построим гистограммы распределения показателя «время пребывания требования в системе» для двух вариантов реализации систем
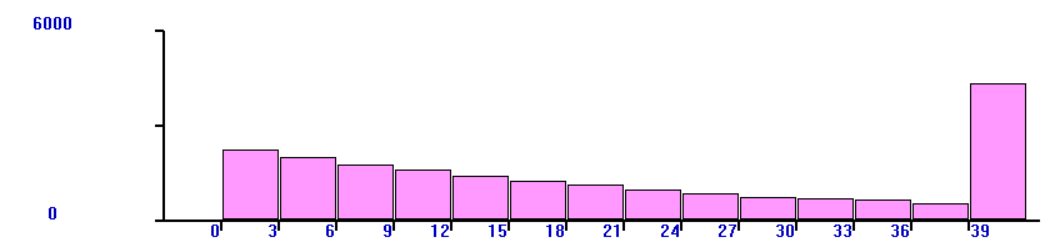
Рис.10. – Гистограмма распределения для 1-го варианта системы
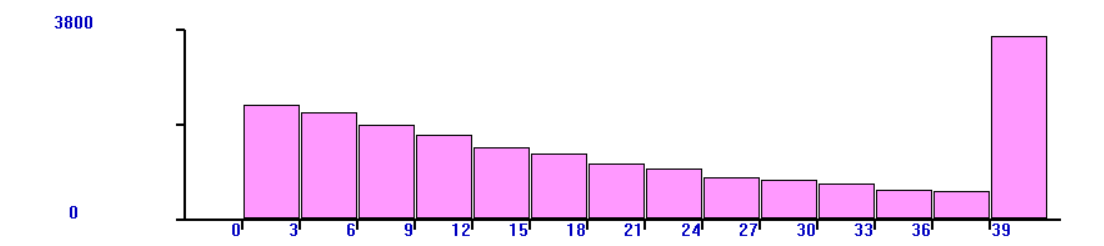
Рис.11. – Гистограмма распределения для 2-го варианта системы
Построим доверительные интервалы Велча для разности средних значений показателя «время пребывания требования в системе» для двух вариантов реализации системы
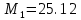
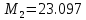
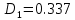
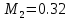
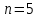
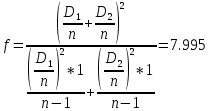
Уровень степеней свободы:
α=0.95
Квантиль Стьюдента:
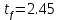
Границы интервала:
-5.5872+-1.188
Доверительный интервал:[-6.772;-4.3992]
Так как данный интервал не переходит через 0, разница в поведении СМО статистически значима.
Вывод :
В результате выполнения данной расчетно-графической работы, было установлено, что уменьшение количества числа рабочих с 6 до 5 увеличило среднее время ожидания заявки в очереди, а изменение интенсивности изготовления деталей ускорило работу данной СМО, то есть, оставив количество рабочих, равное 6, мы добились бы самой оптимальной СМО.
Новосибирск
2021