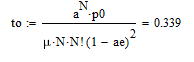Файл: Расчетно графическая работа по дисциплине.docx

Кафедра вычислительной техники



РАСЧЕТНО – ГРАФИЧЕСКАЯ РАБОТА

по дисциплине: моделирование

Выполнил:			Проверил:
Студент гр. АВТ-918 Бахаров А.Н.
			Пинигина Д.Л.
«___» ______ 20__г.			«___» ______ 20__г.
_________________			_________________
(подпись)			(подпись)

Содержание

Цели работы:

- изучить методы аналитического и имитационного моделирования систем на примере решения

конкретной задачи;

- сравнить эффективность использования (простота, точность, объем вычислений)

имитационных и аналитических методов для расчета показателей эффективности СМО;

- изучить методы планирования экспериментов с имитационными моделями СМО на примере решения прикладной задачи.

Часть 1. Моделирование систем массового обслуживания, описываемых случайным процессом «гибели и размножения»

Методы и модели исследования СМО можно условно разбить на аналитические и статистические (имитационного моделирования процессов массового обслуживания).

---

К сожалению, аналитическому решению поддается лишь довольно ограниченный круг задач теории массового обслуживания. Несмотря на постоянно ведущуюся разработку аналитических методов, во многих реальных случаях аналитическое решение либо невозможно получить, либо итоговые зависимости оказываются настолько сложными, что их анализ становится самостоятельной трудной задачей. Поэтому ради возможности применения аналитических методов решения приходится прибегать к различным упрощающим предположениям, что в некоторой степени компенсируется возможностью применения качественного анализа итоговых зависимостей (при этом, разумеется, необходимо, чтобы принятые допущения не искажали реальной картины процесса).

В настоящее время теоретически наиболее разработаны и удобны в практических приложениях методы решения таких задач массового обслуживания, в которых поток требований является простейшим (пуассоновским).

Практическое использование компьютерного имитационного моделирования предполагает построение соответствующей математической модели, учитывающей факторы неопределенности, динамические характеристики и весь комплекс взаимосвязей между элементами изучаемой системы. Имитационное моделирование работы системы начинается с некоторого конкретного начального состояния. Вследствие реализации различных событий случайного характера, модель системы переходит в последующие моменты времени в другие свои возможные состояния. Этот эволюционный процесс продолжается до конечного момента планового периода, т.е. до конечного момента моделирования.

Графы состояний, используемые в моделях систем массового обслуживания, называются схемой гибели и размножения. Такое название обусловлено тем, что эта схема используется в биологических задачах, связанных с изучением численности популяции. Его особенность состоит в том, что все состояния системы можно представить в виде цепочки, в которой каждое из состояний связано с предыдущим и последующим (рис 1).



Рис.1. – Граф состояний в моделях СМО

Задание:

Для системы массового обслуживания, приведенной в варианте (см. ниже), выполнить следующее:

1. Рассчитать вероятности состояний системы и характеристики эффективности СМО аналитически:

---

- определить тип системы массового обслуживания;

- построить размеченный граф состояний системы;

- выбрать расчетные формулы;

- рассчитать следующие показатели эффективности СМО:

• 
  вероятность загрузки системы;
  
• 
  вероятность отказа в обслуживании;
  
• 
  вероятность простоя системы;
  
• 
  вероятность нахождения в системе 1- ой заявки, 2 – х заявок, …, n – заявок;
  
• 
  среднее время обработки одной заявки;
  
• 
  среднее число занятых каналов;
  
• 
  среднее время ожидания в очереди;
  
• 
  среднее число требований в очереди;
  
• 
  среднее число требований в системе;
  
• 
  среднее время нахождения заявки в системе.
  

2. Рассчитать вероятности состояний системы и характеристики эффективности СМО имитационным методом:

- написать программу имитации с использованием GPSS или ExtendSim.

- рассчитать программно показатели эффективности СМО, приведенные в п.1.

3. Сопоставить результаты, полученные на основе использования аналитического и имитационного моделирования. Сделать выводы.

4. Оценить эффективность реализованной в работе системы массового обслуживания.

Сформулировать предложения по улучшению работы СМО.

5. Реализовать имитационное моделирование изучаемой СМО с учетом дополнительных условий (в соответствии с вариантом):

- сымитировать работу системы с учетом дополнительных условий, вычислить вероятность простоя системы, среднее время ожидания в очереди, среднее время пребывания требования в системе по результатам 5-ти прогонов имитационных моделей системы;

- сравнить два варианта реализации системы по результатам 5-ти прогонов (I – исходный, II – с учетом дополнительных условий);

- рассчитать статистические характеристики (среднее, среднеквадратическое отклонение, минимальное и максимальное значения) показателя «время пребывания требования в системе» для двух вариантов реализации системы;

- построить гистограммы распределения показателя «время пребывания требования в системе» для двух вариантов реализации системы;

- построить доверительные интервалы Велча для разности средних значений показателя «время пребывания требования в системе» для двух вариантов реализации системы;

- сравнить два варианта реализации системы, для чего ответить на следующие вопросы. Как введение дополнительных условий повлияло на изменение показателей эффективности функционирования СМО? Какой из вариантов реализации системы более предпочтителен и почему (по каким критериям)?

---

6. Сделать общие выводы по результатам проведенного исследования.

Вариант:

К шести рабочим поступают на изготовление детали с транспортного конвейера. Интервал между поступлениями двух идущих одна за другой деталей равен в среднем: 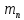=10 минут (закон распределения интервалов показательный). Время изготовления деталей рабочими составляет в среднем: 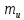=25 минут (закон распределения показательный). При имитационном моделировании задайте количество изготовленных деталей равным 20000.

Дополнительные условия:

• 
  рабочих пять;
  
• 
  интенсивность изготовления деталей рабочими зависит от количества деталей в очереди на обработку: если в очереди 1 деталь, то интенсивность изготовления исходно заданная; если 2 детали, то интенсивность возрастает на 5%; если более двух – на 10%.
  

Ход работы:

Тип системы массового обслуживания – многоканальная система без потерь с неограниченным ожиданием и бесконечным потоком требований на входе (разомкнутая система).




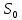
Sj

Sj+l+++++++

=++++++++++j+++1










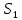
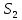
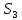
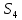
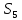
λ λ λ λ λ λ λ λ

---

…

μ 2μ 3μ 4μ 5μ 6μ 6μ 6μ

Рис. 2 – Размеченный граф состояний системы

Вероятность загрузки системы:

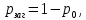где



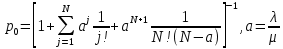
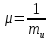=0.04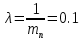







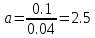
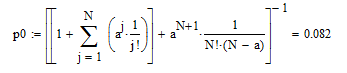
Рис.3 – Расчет p0 средствами Mathcad





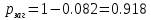
Вероятность отказа в обслуживании:





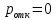
В

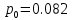
ероятность простоя системы:

Вероятность нахождения в системе 1-ой заявки, 2-х заявок,…, n-заявок:





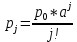
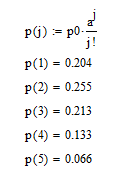
Рис.4. – Расчет pj средствами Mathcad

Среднее время обработки одной заявки:





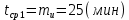
С
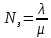=2.5
реднее число занятых каналов:

Среднее время ожидания в очереди:

---