Файл: Курс лекций ульяновск 2016 рекомендовано утверждаю.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 67
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рис. 3. Форма и размеры основной надписи.
а). Образец основной надписи для первого листа документов;
б). Образец формы основной надписи для второго и последующих листов.
Чертёжные шрифты
Шрифт – графическая форма изображения букв, цифр и условных знаков, используемая для выполнения технического документа. Выполнение их должно соответствовать ГОСТ 2.304 – 81.
Размер (номер) шрифта обозначается буквой h и определяется высотой прописных букв в миллиметрах. Размер чертёжного шрифта, т.е. высота букв определена стандартом.
Стандарт устанавливает два типа шрифтов: А и В. В машиностроительном черчении наиболее распространён чертёжный шрифт типа В с наклоном под углом 75о. Толщина линий букв и цифр шрифта Б равна 1/10 h.
Начертание букв русского алфавита прописных и строчных шрифтом типа Б с наклоном, а также арабских цифр, используемых при указании размеров и условных знаков, и также образец надписи приведено на рисунке 4.

Рис. 4. Шрифт чертежный типа Б с наклоном около 75о (ГОСТ 2.304-81*).
Параметры шрифта типа Б с наклоном для букв русского алфавита и арабских цифр в относительных размерах приведены в таблице 4:
Таблица 4
Шрифт типа Б (d = h/10)
| Параметры шрифта | Обозначение | Относительный размер | Размеры, мм | |||||||||
| Размер шрифта | | | | | | | | | | | | |
| высота прописных букв | h | (10/10) h | 10d | 1,8 | 2,5 | 3,5 | 5,0 | 7,0 | 10,0 | 14,0 | 20,0 | |
| высота строчных букв | с | (7/10) h | 7d | 1,3 | 1,8 | 2,5 | 3,5 | 5,0 | 7,0 | 10,0 | 14,0 | |
| Расстояние между буквами | а | (2/10)h | 2d | 0,35 | 0,5 | 0,7 | 1,0 | 1,4 | 2,0 | 2,8 | 4,0 | |
| Минимальный шаг строк (высота вспомогательной сетки) | b | (17/10)h | 17d | 3,1 | 4,3 | 6,0 | 8,5 | 12,0 | 17,0 | 24,0 | 34,0 | |
| Минимальное расстояние между словами | е | (6/10)h | 6d | 1,1 | 1,5 | 2,1 | 3,0 | 4,2 | 6,0 | 8,4 | 12,0 | |
| Толщина линий шрифта | d | (1/10)h | d | 0,18 | 0,25 | 0,35 | 0,5 | 0,7 | 1,0 | 1,4 | 2,0 | |
Тема 1.2. Геометрические построения. Основы проекционного черчения.
1.2.1. Построение перпендикуляров и углов. Способы деления угла, отрезка и окружности на равные части. Сущность проецирования на плоскости. Прямоугольные проекции. Прямоугольное проецирование. Комплексный чертёж. Расположение видов. Аксонометрические проекции.
На практике часто приходится выполнять геометрические построения. Это необходимо не только при составлении чертежа, но и при выполнении разметки перед изготовлением детали, при подготовке инструмента для её контроля в процессе обработки и эксплуатации. Поэтому важно уметь выполнять точные геометрические построения.
Построение перпендикуляров и углов.
Построение прямых углов.
На практике проведение прямой, параллельной заданной, выполняется с помощью чертёжных инструментов: двух угольников или линейки и угольника.
Угол 90° рационально строить с помощью рейсшины и угольника (Рис. 5). Для этого достаточно, проведя прямую линию, восставить к ней перпендикуляр с помощью угольника (Рис. 5, а). Рационально перпендикуляр к отрезку наклонной строить, передвигая (Рис. 5, б) или поворачивая (Рис. 5, в) угольник.
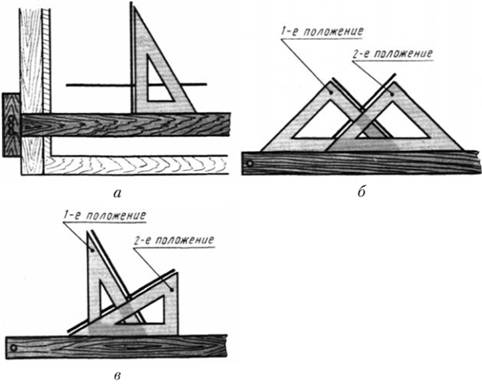
Рис. 5. Построение прямых углов с помощью угольников.
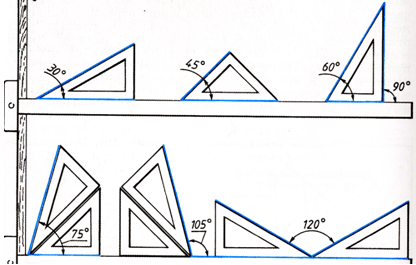
Рис. 6. Построение острых и тупых углов.
Деление отрезка прямой.
Пусть отрезок АВ требуется разделить на пять равных частей. Для этого из любого конца отрезка (из точки А) проведём под острым углом к отрезку прямую линию, на которой откладываем пять равных отрезков произвольной величины. Точку 5 соединяем с точкой В (концом данного отрезка) заданной прямой. Из точек 1, 2, 3, 4 проведём ряд параллельных прямой 5А, которые, пересекая отрезок АВ, разделят его на пять равных частей (Рисунок 7).
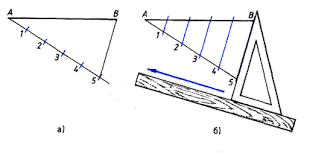
Рис. 7. Деление отрезка на пять равных частей.
Деление окружности на равные части.
Деление окружности на три и шесть равных частей выполняется в следующей последовательности (Рисунок 8а, 8г):
Деление окружности на три равные части производится следующим образом. Точка
А (рис. 8а) принимается за центр, из которого проводится дуга, радиус которой равен радиусу окружности. Проведенная дуга пересечет окружность в точках С и Д. Дуги С-В, В-Д, Д-С являются третьей частью окружности. Соединив точки С, В и Д, получим правильный треугольник (Рисунок 8а).
Деление окружности на 4 равные части. Строим центровые линии, проводим окружность и определяем точки А, В, С, Д (концы диаметров), которые делят окружность на четыре равные части. Соединив отрезками прямых линий найденные точки, получаем правильный четырёхугольник (квадрат), вписанный в окружность (Рисунок 8б).
Деление окружности на пять равных частей выполняется так: находим середину радиуса окружности ОВ (точка Е). Приняв точку В за центр, проведем дугу, радиус которой равен радиусу окружности, до пересечения ее с горизонтальным диаметром в точке О. Отрезок СЕ есть сторона пятиугольника. Отрезок ОЕ соответствует стороне правильного вписанного десятиугольника. Отложив величину, равную 1/5 окружности, разделим ее на пять равных частей. Соединив последовательно засечки (вершины пятиугольника) отрезками прямых линий, получим правильный пятиугольник (Рисунок 8в).
Для деления окружности на шесть равных частей используют равенство сторон правильного шестиугольника радиусу описанной окружности, т. е. если дана окружность , то из концов одного из её диаметров (точек А и Е), как из центров, проводят дуги, равные радиусу окружности. Точки пересечения этих дуг с окружностью разделят её на шесть равных частей. Соединив данные точки отрезками в соответствующей последовательности, получаем правильный шестиугольник, каждая сторона которого равна радиусу окружности (Рисунок 8г).
Зная основы таких построений, можно разделить окружность на любое количество частей, используя правила вписанного и описанного многоугольника.
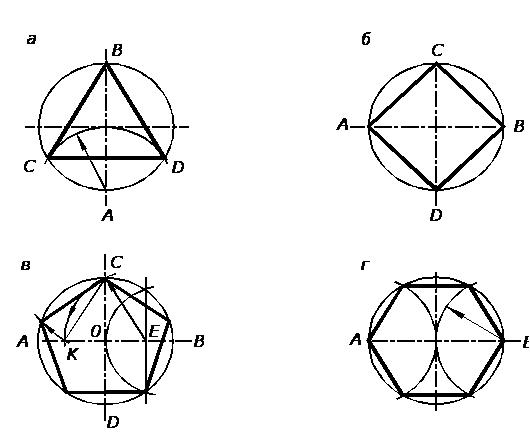
Рис. 8. Деление окружности на части.
Сущность проецирования на плоскости. Прямоугольные проекции. Прямоугольное проецирование.
Изображение пространственного объекта путём проведения линий на плоскости называют чертежом.
Геометрический объект (фигура) – это некоторое множество точек, объединённых между собой определёнными условиями. Для того чтобы отобразить весь геометрический объект, необходимо отобразить каждую из составляющих его точек. Способ, который используется для изображения геометрического объекта, называется
метод проецирования. Результат этого действия называют проекцией.
Прямоугольное проецирование.
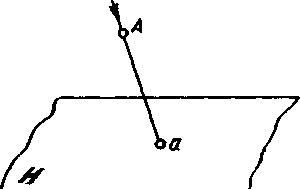
Рис. 9. Проецирование точки на плоскость.
Способ прямого проецирования является одним из приёмов отображения. Пусть в пространстве имеется точка А (Рисунок 9). Для получения проекции (отображения) этой точки на плоскость необходимо провести из неё проецирующий луч перпендикулярно к плоскости. Точка а, в которой проецирующий луч пересекает плоскость проекций, является проекцией точки А на плоскость Н.
Принято использовать систему двух взаимно-перпендикулярных плоскостей проекций, предложенную Г. Монжем в 1799 г. (Рисунок 10). Одна из них, расположенная горизонтально, называется горизонтальной плоскостью проекций, а вторая, расположенная вертикально, - фронтальной плоскостью проекций. Линия пересечения плоскостей (ХО) называется осью проекций (Рисунок 10).
Для получения проекции точки А в системе двух взаимно-перпендикулярных плоскостей выполняют проецирование на каждую плоскость. Пересечение проецирующего луча с горизонтальной плоскостью проекций определяет положение горизонтальной проекции точки а, пересечение проецирующего луча с вертикальной плоскостью проекций даст её фронтальную проекцию а/.
Но пользоваться такими изображениями трудно, поэтому перешли к такому изображению, где обе проекции располагаются в одной плоскости. Для этого горизонтальную и фронтальную плоскости совмещают, т. е. при неподвижной фронтальной плоскости проекций горизонтальную поворачивают вокруг оси Х так, чтобы передняя часть плоскости П1 опустилась (задняя часть плоскости П1 при этом поднимется). После совмещения плоскостей П1 и П2 получим чертёж, показанный на рис.10б. При этом фронтальная и горизонтальная проекции точки располагаются на одной прямой, перпендикулярной к оси x. Прямая а/а называется линией связи. На чертеже сам геометрический объект отсутствует, имеются только его отображения на плоскостях проекций.
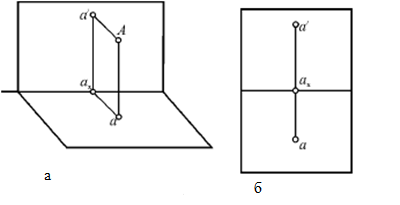
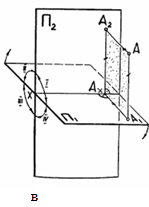
Рис. 10а, б, в. Система двух взаимно-перпендикулярных плоскостей проекций.