Министерство образования Красноярского края

Краевое государственное бюджетное профессиональное образовательное учреждение

«Красноярский колледж радиоэлектроники и информационных технологий»

Отчет по практической работе

Численные методы

дисциплина

Студент	9АБД-2.20					Е.В. Калинникова
	номер группы			подпись, дата				инициалы, фамилия
			оценка
Руководитель от колледжа								А.А. Кетрова
				подпись, дата				инициалы, фамилия

Красноярск 2022

Практическая работа №2-4

Тема: Решение алгебраических и трансцендентных уравнений численными методами.

1. Цель работы: найти приближенное решение уравнения численными методами:

1) дихотомии;

2) простых итераций;

3) Ньютона;

4) секущих;

5) хорд.

2. Оборудование, приборы, аппаратура, материалы: Excel, MathCAD.
Ход работы:

В первую очередь я нашла приближенный интервал изоляции корня. Интервал изоляции корня и исходное уравнение представлены на рисунке 1

---

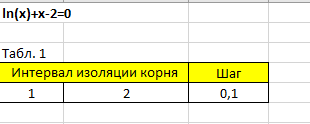
Рисунок 1 – Интервал изоляции корня

Затем пошаговым методом я нашла 2 соседних корня, функции которых имеют разные знаки, шаг корней составил 0,1. Пошаговый метод представлен на рисунке 2.



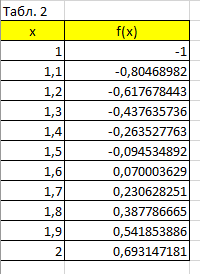
Рисунок 2 – Пошаговый метод

1. 
   Начала решать уравнение методом Ньютона.
   

С помощью проверки условий сходимости я нашла начальное приближенное. Для этого нашла функцию и производную обоих корней, после чего перемножила их, корень, произведение функции и производной которого будет больше 0, является приближенным значением. Решение представлено на рисунке 3.



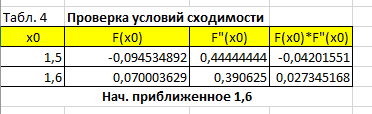
Рисунок 3 – Проверка условий сходимости

Нашла функцию и производную корня, после чего по формулам метода Ньютона нашла значение, которое подставила как новое значение корня. Повторяла цикл пока точность корня не составила 0,0001. Результат представлен на рисунке 4.



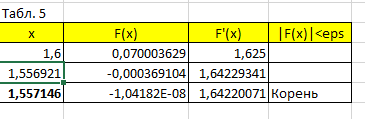
Рисунок 4 – Метод Ньютона

2. 
   Начала решать уравнение методом дихотомии.
   

Сначала нашла середину отрезка, концами которого являются интервалы изоляции корня, затем нашла функции концов и середины отрезка, функции, значения которых имеют разные знаки, будут составлять новый отрезок.

Продолжила цикл до тех пор, пока разность концов отрезка не достигла 0,0001 или меньше. Результат представлен на рисунке 5.



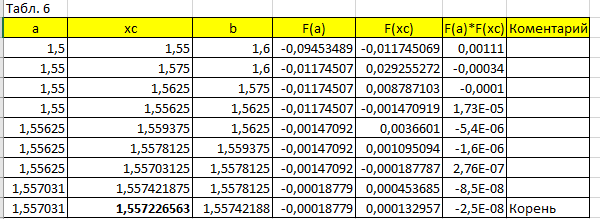
Рисунок 5 – Метод дихотомии

3. 
   Начала решать уравнение методом простой итерации.
   

В первую очередь я нашла приведенное уравнение и сделала проверку сходимости, полученное значение, которое ближе к 0, будет являться начальным приближенным значением. Приведенное уравнение и проверка сходимости представлены на рисунке 6.

---

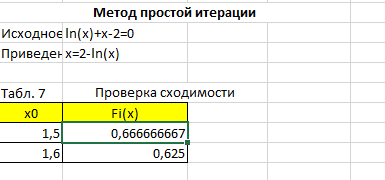
Рисунок 6 – Приведенное уравнение и проверка сходимости

Дальше я нашла, функцию начального приближенного и его фи, после чего подставила фи на место начального приближенного и повторяла операцию до тех пор, пока разность между х и фи не достигла 0,0001 или меньше. Результат представлен на рисунке 7.



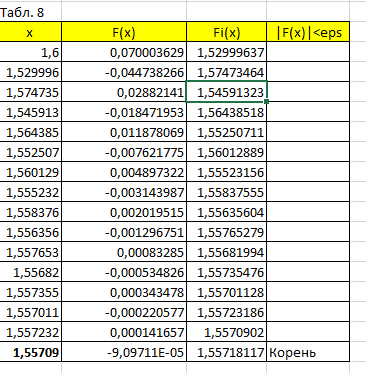
Рисунок 7 – Приведенное уравнение и проверка сходимости

4. 
   Начала решать уравнение методом хорд.
   

Нашла функции интервалов изоляции корня, затем по формуле методов хорда нашла значение, которое подставила на место х, продолжила выполнять цикл пока разность значений х не достигла 0,0001 или меньше. Результат представлен на рисунке 8.



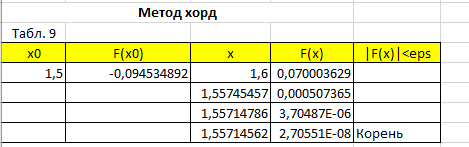
Рисунок 8 – Метод хорд

5. 
   Начала решать уравнение методом секущих.
   

Нашла функции интервалов изоляции корня, дальше по формуле метода секущих нашла значение, которое подставила как новое значение х, продолжила повторять цикл, до тех пор, пока разность значений х не достигла 0,0001 или меньше. Результат представлен на рисунке 9.



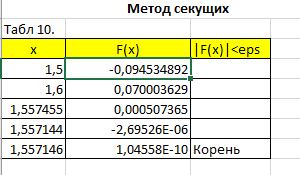
Рисунок 9 – Метод секущих

Практическая работа №5

Тема: Решение систем линейных уравнений приближёнными методами. Метод итераций.

1. Цель работы: найти приближенное решение системы линейных уравнений численным методом простых итераций.

2. Оборудование, приборы, аппаратура, материалы: Excel, MathCAD.
Ход работы:

Составила матрицу. Матрица представлена на рисунке 10.



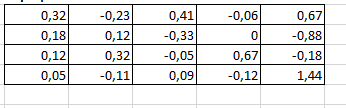
Рисунок 10 – Матрица

Начала решать систему линейных уравнений методом простых итераций.

За начальные значения всех х взяла 0, после чего подставив 0 в уравнения нашла значение, которое так же подставила вместо х, продолжила выполнять цикл до тех пор, пока разность значений х всех линейных уравнений не достигла 0,0001 или меньше. Значения х берем из одной итерации. Результат представлен на рисунке 11.

---

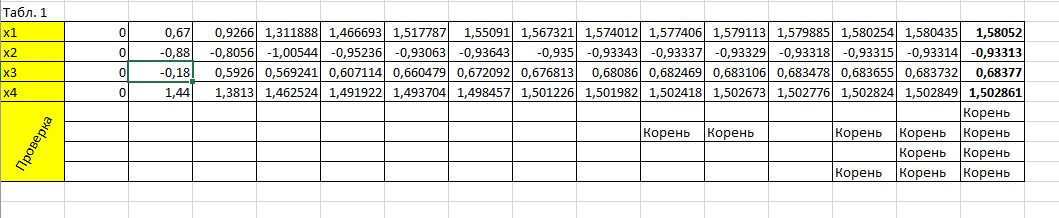
Рисунок 11 – Метод простых итераций

Практическая работа №6

Тема: Решение систем линейных уравнений приближёнными методами. Метод Зейделя.

1. Цель работы: найти приближенное решение системы линейных уравнений численным методом Зейделя.

2. Оборудование, приборы, аппаратура, материалы: Excel, MathCAD.
Ход работы:

Составила транспортированную матрицу. Матрица представлена на рисунке 12.



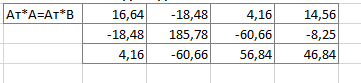
Рисунок 12 – Транспортированная матрица

За начальные значения всех х взяла 0, после чего подставив 0 в уравнения нашла значение, которое так же подставила вместо х, продолжила выполнять цикл до тех пор, пока разность значений х всех линейных уравнений не достигла 0,0001 или меньше. Значения х берем каждое найденное предыдущее. Результат представлен на рисунке 13.



Рисунок 13 – Метод Зейделя

Практическая работа №7-8

Тема: Составление интерполяционных формул Лагранжа. Оценка погрешности интерполирования функции.

1. 
   Цель работы:
   

1. 
   вычислить значение функции f(x) в заданной точке а с помощью интерполяционного полинома Лагранжа;
   
2. 
   рассчитать абсолютную погрешность вычислений и дать оценку сверху найденному приближенному решению;
   
3. 
   построить графики полинома Лагранжа
   

2. Оборудование, приборы, аппаратура, материалы: Excel, MathCAD.
Ход работы:

В первую очередь записала значения в удобной форме. Задание и таблица значений представлены на рисунках 14 и 15 соответственно.



Рисунок 14 – Задание



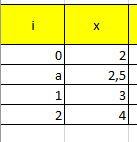
Рисунок 15 – Таблица значений

Нашла функцию х и по формуле вычислила полином Лагранжа. Результат представлен на рисунке 16.



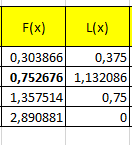
Рисунок 16 – Функции и полином Лагранжа
Затем, возведя в модель разность функции и полинома Лагранжа, решила это выражение и получила погрешность решения, после чего по формуле нахождения оценки сверху нашла максимально допустимую погрешность. Вывела график полинома Лагранжа выражения. Результаты представлены на рисунке 17.

---

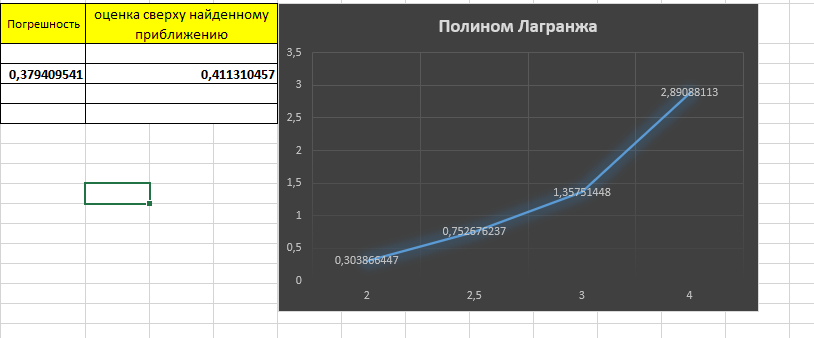
Рисунок 17 – Полином Лагранжа

Практическая работа №9-11

Тема: Составление интерполяционных формул Лагранжа. Оценка погрешности интерполирования функции.

1. Цель работы: для функции f (x) построить таблицу значений для n = 4 и найти значение определенного интеграла на отрезке [2;4], используя формулы методов:

1. 
   Ньютона-Котеса;
   
2. 
   Прямоугольников;
   
3. 
   Трапеций;
   
4. 
   Симпсона
   

2. Оборудование, приборы, аппаратура, материалы: Excel, MathCAD.
Ход работы:

В первую очередь нашла интервал изоляции корня, записала значения в удобной форму и нашла функции. Результат представлен на рисунке 18.



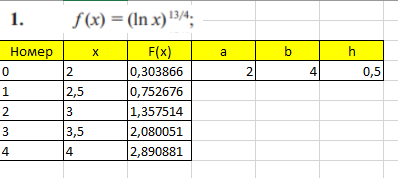
Рисунок 18 – Приготовления

1. 
   Начала решать методом левых прямоугольников.
   

Сложила все функции кроме последней и умножила на h. Результат представлен на рисунке 19.



Рисунок 19 – Метод левых прямоугольников

2. 
   Начала решать методом правых прямоугольников.
   

Сложила все функции кроме первой и умножила на h. Результат представлен на рисунке 20.


Рисунок 20 – Метод правых прямоугольников

3. 
   Начала решать методом центральных прямоугольников.
   

Поделила h на 2 и прибавила к первому значению х, затем нашла функцию этого значения, провела такую же операцию со следующими значениями х кроме последнего. Все полученные функции сложил и умножил на h. Результат представлен на рисунке 21.



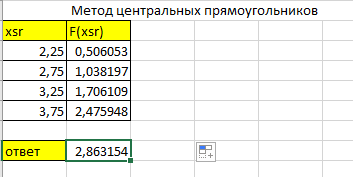
Рисунок 21 – Метод центральных прямоугольников

4. 
   Начала решать методом трапеций.
   

Сумму всех функции умножила на h и поделила на 2, после чего прибавила сумму функции, в которую не входил первая и последняя функции. Результат представлен на рисунке 22.



Рисунок 22 – Метод трапеций

5. 
   Начала решать методом парабол.
   

---

Смотрите также файлы

• Книга представляет собой исходные принципы даосской онтологии. Дао это понятие, при помощи которого возможно дать универсальный, всеобъемлющий ответ на вопрос о происхождении и способе существования всего сущего..docx

• Гости из картыменю блюд и напитков выбирают то, что им больше всего нравится.docx

• Таырыбы Бірфазалыекі.docx

• Приборы радиационной, химической разведки и дозиметрического контроля.docx

• Отчет по лабораторной работе 1 Получение гидроксидов никеля (II) и цинка исследование их кислотноосновных свойств.doc