2 (базовый уровень, время – 3 мин)

Тема: Анализ таблиц истинности логических выражений.Что проверяется:Умение строить таблицы истинности и логические схемы.1.5.1. Высказывания, логические операции, кванторы, истинность высказывания1.1.6. Умение строить модели объектов, систем и процессов в виде таблицы истинности для логического высказыванияПро обозначенияК сожалению, обозначения логических операций И, ИЛИ и НЕ, принятые в «серьезной» математической логике (,,¬), неудобны, интуитивно непонятны и никак не проявляют аналогии с обычной алгеброй. Автор, к своему стыду, до сих пор иногда путает  и . Поэтому на его уроках операция «НЕ» обозначается чертой сверху, «И» – знаком умножения (поскольку это все же логическое умножение), а «ИЛИ» – знаком «+» (логическое сложение). В разных учебниках используют разные обозначения. К счастью, в начале задания ЕГЭ приводится расшифровка закорючек (,,¬), что еще раз подчеркивает проблему. Что нужно знать:

• 
  условные обозначения логических операций
  

¬A, не A (отрицание, инверсия)AB, A и B (логическое умножение, конъюнкция)AB, A или B (логическое сложение, дизъюнкция)A → B импликация (следование)A  B эквивалентность (равносильность)

• 
  операцию «импликация» можно выразить через «ИЛИ» и «НЕ»:
  

A → B=¬AB или в других обозначениях A → B=

• 
  иногда для упрощения выражений полезны формулы де Моргана:
  

¬ (A  B) = ¬A  ¬B

---

¬ (A  B) = ¬A  ¬B

• 
  если в выражении нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», «импликация», и самая последняя – «эквивалентность»
  
• 
  таблица истинности выражения определяет его значения при всех возможных комбинациях исходных данных
  
• 
  если известна только часть таблицы истинности, соответствующее логическое выражение однозначно определить нельзя, поскольку частичной таблице могут соответствовать несколько разных логических выражений (не совпадающих для других вариантов входных данных);
  
• 
  количество разных логических выражений, удовлетворяющих неполной таблице истинности, равно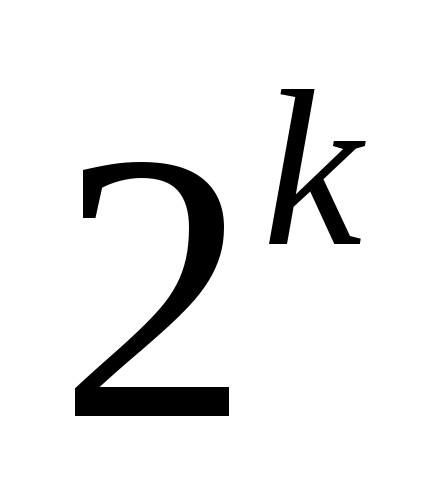 , где 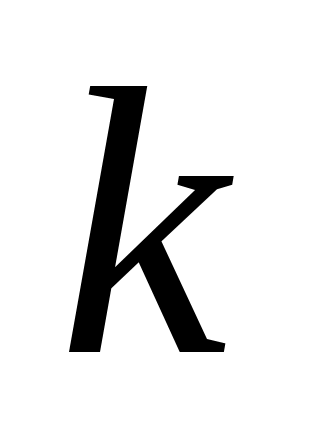– число отсутствующих строк; например, полная таблица истинности выражения с тремя переменными содержит 2³=8 строчек, если заданы только 6 из них, то можно найти 2^8-6=2²=4 разных логических выражения, удовлетворяющие этим 6 строчкам (но отличающиеся в двух оставшихся)
  
• 
  логическая сумма A + B + C + … равна 0 (выражение ложно) тогда и только тогда, когда все слагаемые одновременно равны нулю, а в остальных случаях равна 1 (выражение истинно)
  
• 
  логическое произведение A · B · C · … равно 1 (выражение истинно) тогда и только тогда, когда все сомножители одновременно равны единице, а в остальных случаях равно 0 (выражение ложно)
  
• 
  логическое следование (импликация) А→В равна 0 тогда и только тогда, когда A (посылка) истинна, а B (следствие) ложно
  
• 
  эквивалентность АB равна 1 тогда и только тогда, когда оба значения одновременно равны 0 или одновременно равны 1
  

---

Пример задания:

Р-22 (демо-2021). Логическая функция F задаётся выражением (x  y)  ¬(y  z)  ¬w.На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

?	?	?	?	F
1		1		1
0	1		0	1
	1	1	0	1

В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.Решение (построение таблицы истинности для F = 1):

1. 
   перепишем выражения в виде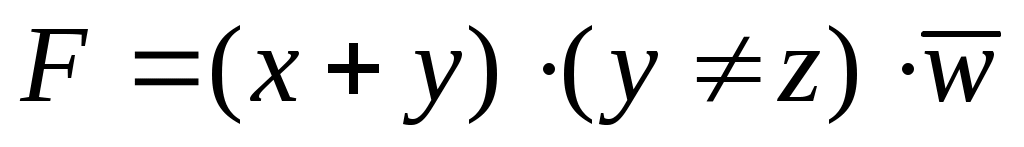
   
2. 
   поскольку имеем логическое произведение значение w обязательно должно быть равно 0, то есть, в столбце w таблицы должны быть все нули; это возможно только в последнем столбце:
   

   ?	?	?	w	F
   1		1	0	1
   0	1		0	1
   	1	1	0	1

3. 
   теперь определим все комбинации переменных, для которых функция равна 1 (их не должно быть много!)
   
4. 
   чаще всего в выражении встречается переменная y, поэтому мы сначала примем y = 0, а затем – y = 1.
   
5. 
   при y = 0 (и w = 0) получаем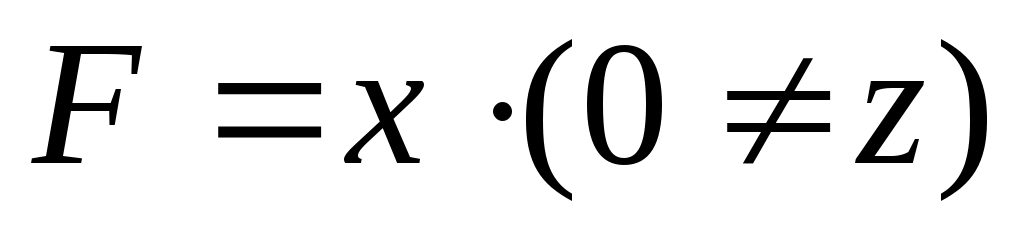 , что справедливо только при x = 1и z = 1:
   

   x	y	z	w	F
   1	0	1	0	1

6. 
   при y = 1 (и w = 0) получаем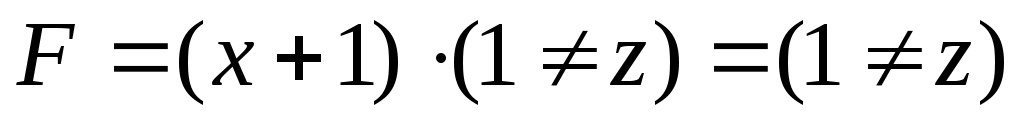 , что справедливо при z = 0 и любом x, это даёт ещё два варианта:
   

   x	y	z	w	F
   0	1	0	0	1
   1	1	0	0	1

7. 
   объединим три полученных строки:
   

   x	y	z	w	F
   1	0	1	0	1
   0	1	0	0	1
   1	1	0	0	1

8. 
   видим, что в столбце z должна быть одна единица и два нуля, это возможено только в первой строке исходной таблицы:
   

   z	?	?	w	F
   1		1	0	1
   0	1		0	1
   0	1	1	0	1

9. 
   при z = 1нужно, чтобы y = 0, поэтому второй столбец – это y, а третий – x:
   

   z	y	x	w	F
   1	0	1	0	1
   0	1	0	0	1
   0	1	1	0	1

10. 
    Ответ: zyxw.
    

---

Решение (построение таблицы с помощью электронных таблиц, П.Е. Финкель, г. Тимашевск)

1. 
   поскольку во время компьютерного экзамена есть возможность использовать электронные таблицы, можно построить таблицу истинности с их помощью
   
2. 
   заполняем первую часть таблицы, перечисляя все комбинации переменных в порядке возрастания двоичного кода:
   

3. 
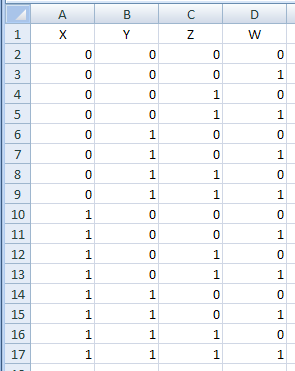
   для каждой строчки определяем выражения, входящие в логическое произведение, а затем – значение функции:
   

4. 
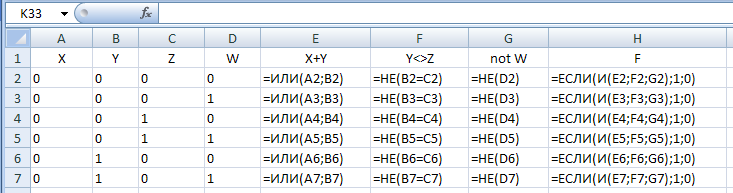
   сортируем строки таблицы по столбцу H по убываниию:
   

5. 
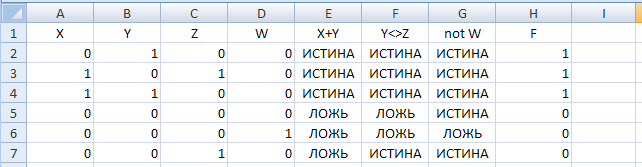
   удаляем строки, где функция равна 0; можно также скрыть вспомогательные столбцы E, F, G:
   

6. 
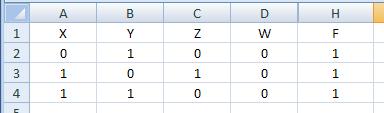
   дальше рассуждаем так же, как и при теоретическом решении
   
7. 
   Ответ: zyxw.
   

Решение (построение таблицы с помощью программы, А.С. Гусев, г. Москва, https://youtu.be/RRL1Wal9ImU):

1. 
   поскольку во время компьютерного экзамена есть возможность использовать среды программирования, для построения частичной таблицы истинности (всех строк, при которых F=1) можно написать переборную программу на Python
   
2. 
   перебор выполняем во вложенном цикле:
   

for x in 0, 1:for y in 0, 1:for z in 0, 1:for w in 0, 1:# вычисление функции F# вывод (x, y, z, w), если F=1

3. 
   для вычисления значения функции необходимо понимать, как логические операторы записываются на языке программирования; в Python их можно реализовать следующим образом:
   

∧ конъюнкция andдля языков, где логическое значение True воспринимается как 1, а False – как 0, можно использовать обычное умножение *∨ дизъюнкция or¬ отрицания not()≡ тождество ==⊕ строгая дизъюнкция !=→ импликация – для импликации в python оператора нет, но импликацию можно преобразовать в дизъюнкцию; например, a → b можно записать как ¬a ∨ b, а это в свою очередь записать как

---

not(a)or b, not a or b или a <= b

4. 
   Запишем нашу функцию на языке программирования:
   

F = (x or y) and not(y == z) and not(w)

5. 
   чтобы выводить не полную таблицу истинности, а только те строки, в которых функция равна 1, добавим условие вывода:
   

ifF: # то же самое, что "ifF == True:"print(x, y, z, w)

6. 
   Приведём полную программу:
   

print('x y z w')for x in 0, 1:for y in 0, 1:for z in 0, 1:for w in 0, 1:F = (x or y) and not(y == z) and not(w)if F:print(x, y, z, w)

7. 
   после запуска программы получаем все интересующие нас строки:
   

x y z w0 1 0 01 0 1 01 1 0 0

8. 
   дальше рассуждаем так же, как и в приведённом выше теоретичеком решении
   
9. 
   Ответ: zyxw.
   

Решение (прямой перебор, А. Богданов):

1. 
   в принципе, можно написать программу, которая сразу выдает решение этого задания прямым перебором вариантов
   
2. 
   Часть 1: https://www.youtube.com/watch?v=yX5oSYtM5E0
   
3. 
   Часть 2: https://www.youtube.com/watch?v=eSkrt4KrsmU
   
4. 
   Ответ: zyxw.
   

---

Смотрите также файлы

• А) отдельных категорий административных дел (разд. Iv.pdf

• Конспект содержания программы Инклюзивное и интегративное образование детей с овз в условиях введения и реализации фгос ноо овз.doc

• 13. 03. 02 Электроэнергетика и электротехника.docx

• Искусственный интеллект его возможности и потенциал.docx

• Анализ содержания организации и руководства игровой деятельности детей дошкольного возраста в режиме дня доо в группах детей раннего, младшего и старшего дошкольного возраста..docx