Ещё пример задания:

Р-21. Логическая функция F задаётся выражением

((x  ¬y)  (w  z))  (z  x).

На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

?	?	?	?	F
	0	0	1	1
0	1	0	0	1
0			1	1

В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Решение (построение таблицы истинности для F = 1):

1. 
   перепишем выражение, раскрыв импликацию по формуле :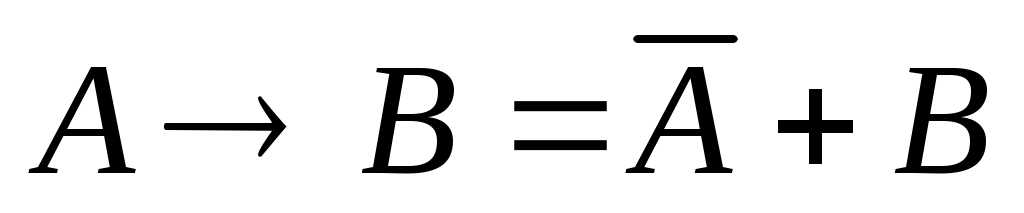
   
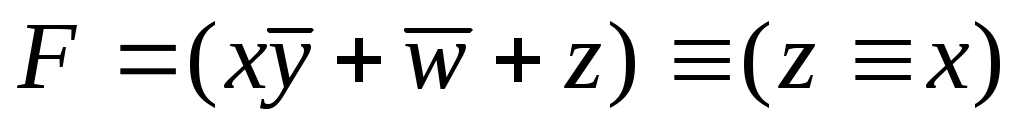
2. 
   сначала предположим, что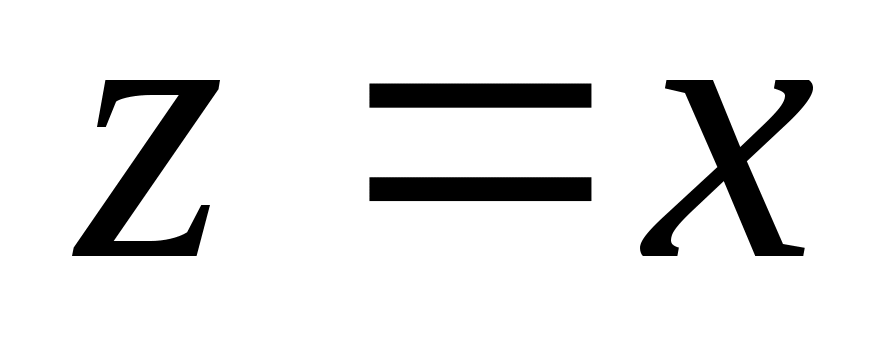 ; в этом случае получаем
   

3. 
   так как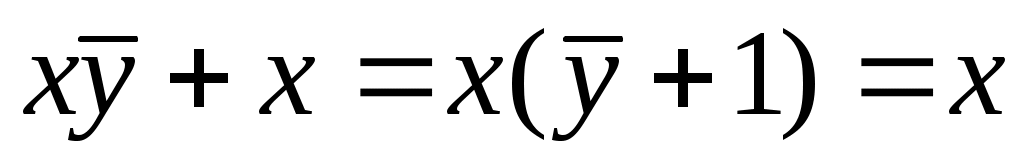 , получим 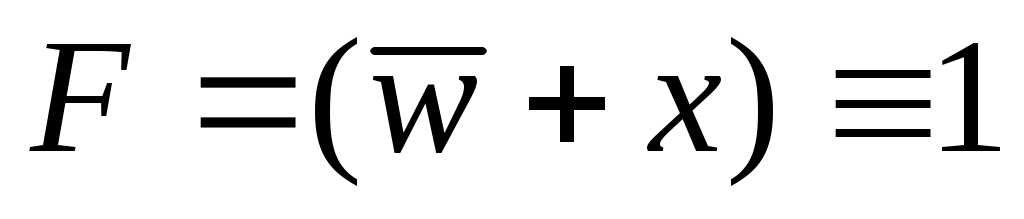; при этом значение y может быть любым (1 или 0)
   
4. 
   теперь пусть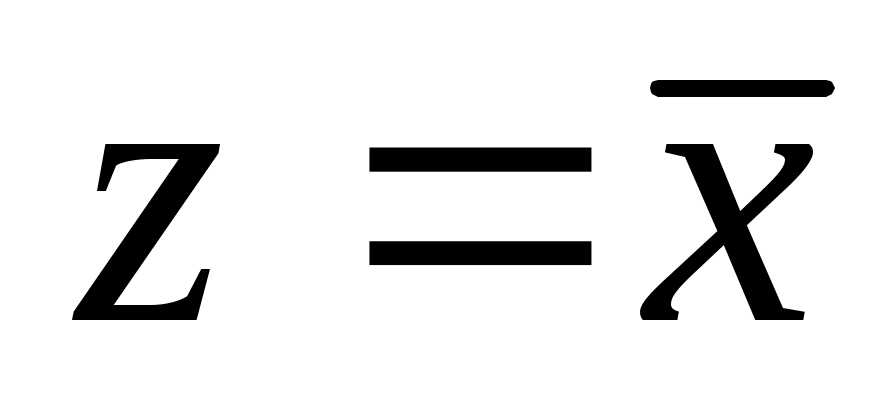 , тогда получаем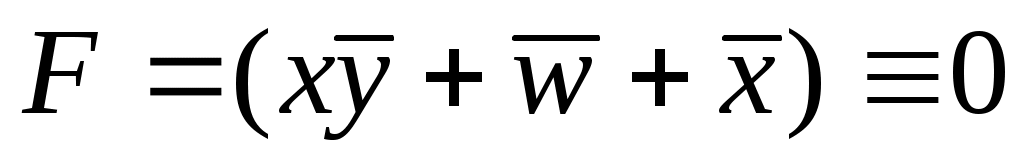
   
5. 
   используем распределительный закон: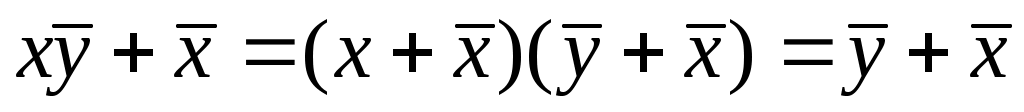 , так что
   

, откуда сразу следует

---

и – единственный вариант!

6. 
   этот единственный вариант, для которого , ОБЯЗАТЕЛЬНО должен быть в приведённой таблице, потому что иначе мы не сможем различить столбцы z и x; это может быть только последняя строчка, куда нужно добавить две единицы:
   

   z	?	?	?	F
   	0	0	1	1
   0	1	0	0	1
   0	1	1	1	1

7. 
   в остальных строчках должно вполняться равенство , значит x – точно не второй столбец (не подходит вторая строка)
   
8. 
   предположим, что x – третий столбец, и в свободной ячейке – нуль:
   

   z	?	x	?	F
   0	0	0	1	1
   0	1	0	0	1
   0	1	1	1	1

9. 
   при этом для остальных двух столбцов в этих строчках должно выполняться условие , а оно не может выполняться – при любом варианте в одной строке сумма 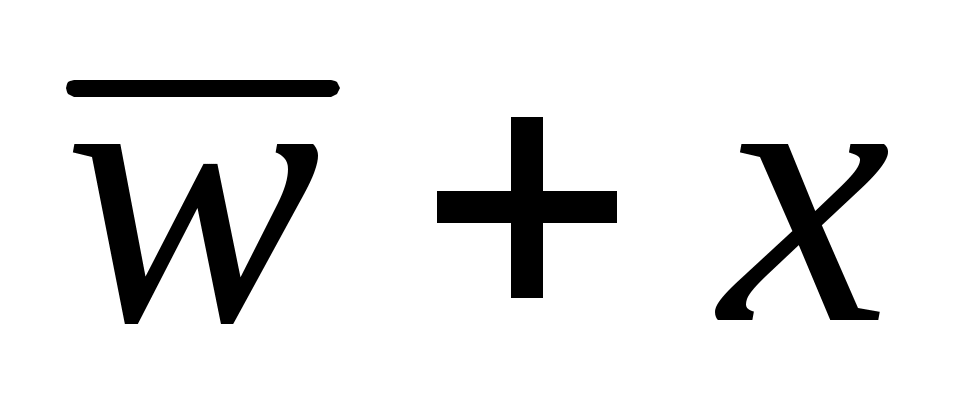равна 0; значит x – последний столбец, и в первой строке z = 1:
   

   z	?	?	x	F
   1	0	0	1	1
   0	1	0	0	1
   0	1	1	1	1

10. 
    чтобы разобраться с поcледними двумя столбцами снова вспомним, что при должно выполняться условие ; это возможно только тогда, когда второй столбец – это y, а третий - w
    
11. 
    Ответ: zywx
    

---

Решение (А.Н. Носкин, заполнение исходной ТИ и анализ полной таблицы истинности для F = 1):

1. 
   в выражении 4 логических переменных, тогда всех решений будет 16 (2⁴).
   

x	y	w	z
0	0	0	0
0	0	0	1
0	0	1	0
0	0	1	1
0	1	0	0
0	1	0	1
0	1	1	0
0	1	1	1
1	0	0	0
1	0	0	1
1	0	1	0
1	0	1	1
1	1	0	0
1	1	0	1
1	1	1	0
1	1	1	1

2. 
   подставим набор значений логических переменных и удалим все решения, которые не дают в ответе F = 1
   

x	y	w	z
0	0	0	0
0	1	0	0
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	0
1	1	1	1

---

Получаем 7 решений. Анализируя ТИ исходной функции видим, что набора 0 0 0 0 и 1 1 1 1 нет. Уберем их из ТИ решений.

x	y	w	z
0	1	0	0
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	0

3. 
   В ТИ решений только одна строка имеет три нуля, тогда сравнивая с ТИ исходной функции видим, что 1 соответствует Y.
   

?	Y	?	?	F
	0	0	1	1
0	1	0	0	1
0			1	1

4. 
   ДОЗАПОЛНИМ таблицу истинности исходной функции (желтая заливка) на основе анализа ТИ решений, а именно т.к больше строк с тремя «0» нет, то в первой строке в пустой ячейке будет «1». И раз нет больше строк с двумя «0», то в третьей строке пустые ячейки равны «1».
   

?	Y	?	?	F
1	0	0	1	1
0	1	0	0	1
0	1	1	1	1

---

5. 
   Анализируя 1ю строку выше приведенной таблице и ТИ решений видим, что строка с двумя «0» всего одна, из которых один нуль известен - это Y, тогда второй это – W;
   

?	Y	W	?	F
1	0	0	1	1
0	1	0	0	1
0	1	1	1	1

6. 
   Далее рассуждая видим, что в ТИ решений (кроме столбца Y) один «0» имеет – Х, тогда последний столбец – это Х, а первый столбец – Z.
   
7. 
   Ответ: zywx
   

Решение (построение таблицы с помощью программы, Б.С, Михлин)

print ('x y w z') # заголовок таблицы (в алфавитном порядке)

k = 0, 1 # k - кортежконстант (0 - False, 1 - True)

for x in k:

for y in k:

for w in k:

for z in k:

if (x and not y or (not w or z)) == (z == x):

# можнокороче:

# if (x and not y or (w <= z)) == (z == x):

print(x, y, w, z) # если F = 1

---

Смотрите также файлы

• А) отдельных категорий административных дел (разд. Iv.pdf

• Конспект содержания программы Инклюзивное и интегративное образование детей с овз в условиях введения и реализации фгос ноо овз.doc

• 13. 03. 02 Электроэнергетика и электротехника.docx

• Искусственный интеллект его возможности и потенциал.docx

• Анализ содержания организации и руководства игровой деятельности детей дошкольного возраста в режиме дня доо в группах детей раннего, младшего и старшего дошкольного возраста..docx