Ещё пример задания:

Р-20. Логическая функция F задаётся выражением

((x  y)  (y  z))  ((x  w)  (w  z)).

На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

?	?	?	?	F
0	1	1	1	1
0	1	0		1
0	1	0		1

В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Решение (построение таблицы истинности для F = 1):

1. 
   запишем выражение в более понятной форме: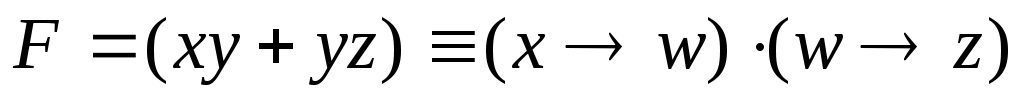
   
2. 
   попробуем найти все сочетания переменных, при которых функция равна 1 (их должно быть не очень много)
   
3. 
   при x = 0 получаем ; импликация с нулём в левой части всегда истинна (из лжи следует всё, что угодно), поэтому
   
4. 
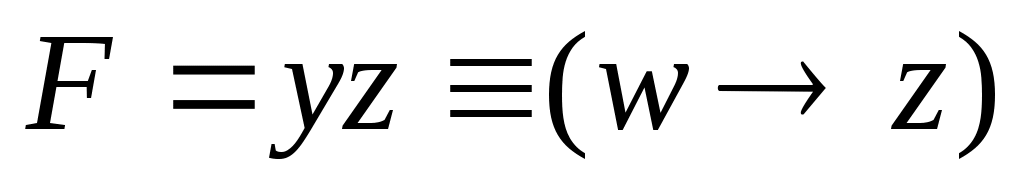
   пусть теперь ещё z = 0, тогда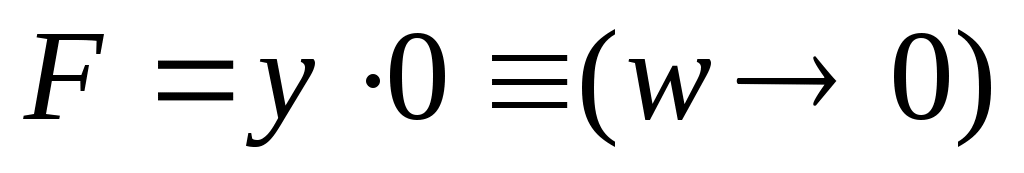 , что истинно при w = 1 и при любом y;
   
5. 
   пусть теперь x = 0 и z = 1, тогда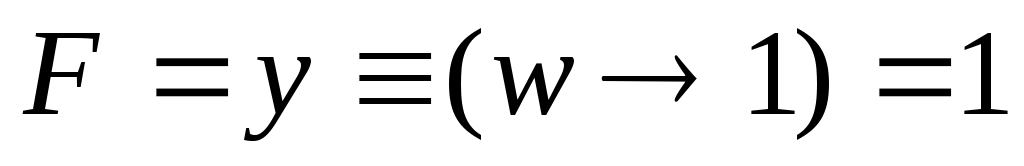 , что истинно при y = 1 и при любом w;
   
6. 
   из 4 и 5 получаем такие строки в таблице истинности исходной функции:
   

   x	y	z	w	F
   0	0	0	1	1
   0	1	0	1	1
   0	1	1	0	1
   0	1	1	1	1

7. 
   остаётся рассмотреть случай, когда x = 1, при этом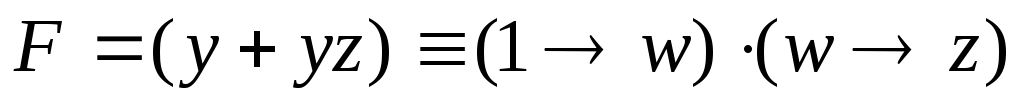
   
8. 
   учитываем, что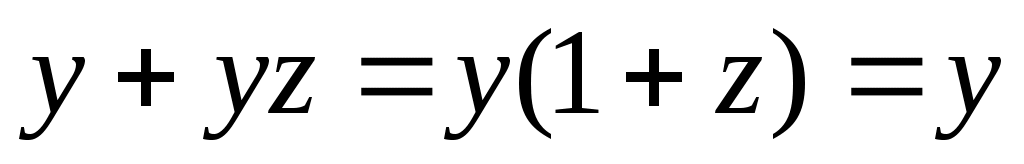 и 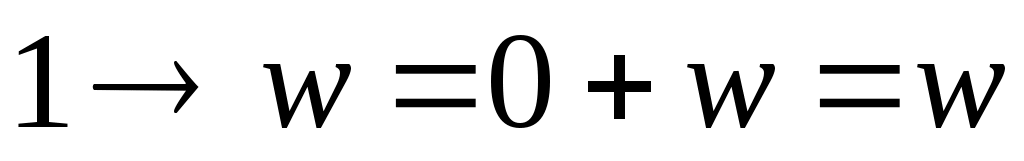; получаем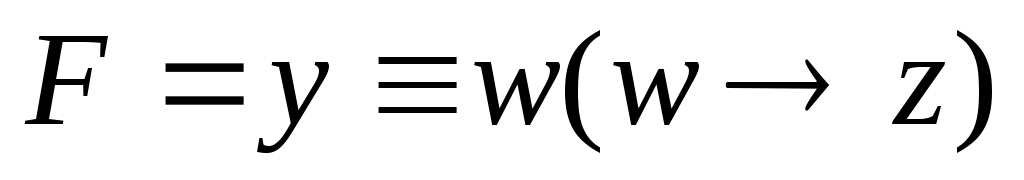
   
9. 
   преобразуем импликацию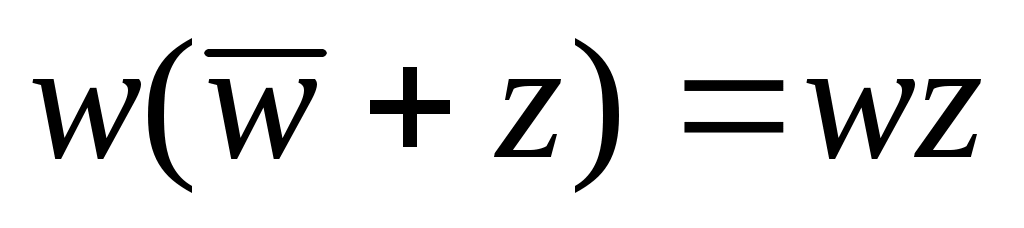 , так что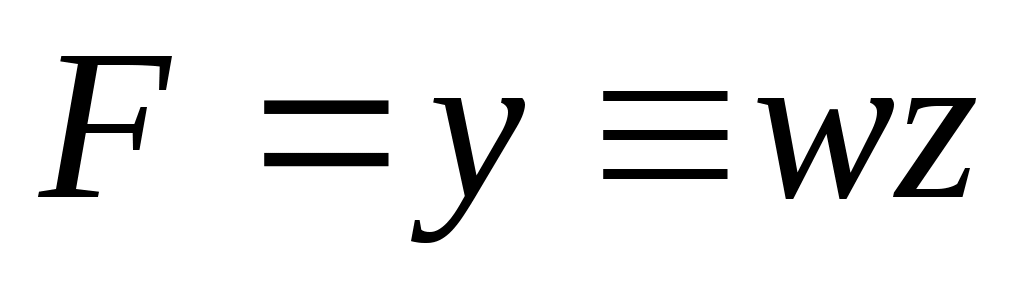
   
10. 
    для y = 0 это выражение истинно при (w, z) = (0,0), (0,1) и (1,0), а для y = 1 – только при w = z = 1, это даёт ещё 4 строки в таблице истинности
    

    x	y	z	w	F
    1	0	0	0	1
    1	0	0	1	1
    1	0	1	0	1
    1	1	1	1	1

11. 
    итак, у нас есть 8 строк в таблице истинности, где функция равна 1:
    

---

x	y	z	w	F
0	0	0	1	1
0	1	0	1	1
0	1	1	0	1
0	1	1	1	1
1	0	0	0	1
1	0	0	1	1
1	0	1	0	1
1	1	1	1	1

попробуем сопоставить их с заданными в условии строками:

?	?	?	?	F
0	1	1	1	1
0	1	0		1
0	1	0		1

12. 
    замечаем, что есть одна характерная строка с тремя единицами; кроме того, поскольку все строки различны, в одной из пустых ячеек должен стоять 0, а во второй – 1
    
13. 
    в полученной нами таблице видим единственную строку с тремя единицами, что сразу позволяет определить, что первый столбец – это x, который всегда равен 0:
    

    x	y	z	w	F
    0	0	0	1	1
    0	1	0	1	1
    0	1	1	0	1
    0	1	1	1	1

14. 
    теперь из оставшихся двух строк остаётся найти 2 строки, значения которых различаются только в одном столбце; под это условие подходит только пара двух верхних строк, они различаются в столбце y – из исходной таблицы видим, что это 4-й столбец
    
15. 
    также из исходной таблицы видим, что во втором столбце в этих двух строках единицы – это w, тогда третий столбец – это z
    
16. 
    Ответ: xwzy.
    

---

Решение (А.Н. Носкин, построение таблицы истинности для F = 1):

1. 
   запишем выражение в более понятной форме:
   
2. 
   вынесем y за скобки: F = (y*(x+z) ≡ ((x→w)*(w→z))
   
3. 
   F = 1, при 0=0 и 1=1. Тогда составим ТИ для левой части выражения равные 0 и 1.
   

y	x	z
0	0	0
0	0	1
0	1	0
0	1	1
1	0	0

y	x	z
1	0	1
1	1	0
1	1	1

4. 
   Объединим эти таблицы, подключим переменную w и уберем из таблицы строки, при которых F=0 после подключения переменной w.
   

   y	x	z	w
   0	0	0	1
   0	1	0	0
   0	1	0	1
   0	1	1	0
   1	0	0	1
   1	0	1	0
   1	0	1	1
   1	1	1	1

5. 
   Получилось 8 всевозможных решений.
   
6. 
   Обратим внимание, что по условию у нас нет повторяющихся строк, но в таблице есть строки с тремя одинаковыми ячейками, тогда можно ДОЗАПОЛНИТЬ таблицу истинности исходной функции (желтая заливка) в одну из них вставив 0, в другую 1.
   

   ?	?	?	?	F
   0	1	1	1	1
   0	1	0	1	1
   0	1	0	0	1

7. 
   Анализ строк таблицы истинности исходной функции показывает:
   

---

- строки, состоящей из четырех «1» нет, поэтому ее можно убрать (красная заливка);

- только одна строка имеет в ячейках три единицы и один «0». И в ТИ всех решений (желтая заливка) этот «0» будет соответствовать Х в ТИ исходной функции.

y	x	z	w
0	0	0	1
0	1	0	0
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	0	1	1
1	1	1	1

8. 
   Так как мы определили, что первый столбец соответствует Х и содержит только «0», то строки ТИ решений с «1» в столбце Х – удалим (синяя заливка)
   

y	x	z	w
0	0	0	1
0	1	0	0
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	0	1	1
1	1	1	1

---

и получим ТИ меньшего размера.

y	x	z	w
0	0	0	1
1	0	0	1
1	0	1	0

9. 
   Анализ столбцов ТИ исходной функции показывает, что одна «1» в третьем столбце соответствует Z, а в третьей строке ТИ исходной функции две неизвестные переменные противоположны «0» и «1», что соответствует W и Y, так как X и Z уже определены и равны «0» (зеленая заливка)
   

y	x	z	w
0	0	0	1
1	0	0	1
1	0	1	0

10. 
    Ответ: xwzy.
    

Решение (построение таблицы с помощью программы, Б.С, Михлин)

print('x y z w') # заголовок таблицы

k = 0, 1 # k - кортежконстант (0 - False, 1 - True)

for x in k:

for y in k:

for z in k:

for w in k:

if (x and y or y and z) == ((not x or w) \

and (not w or z)):

# можнокороче:

# if ( x * y or y * z ) == ( x <= w)*( w <= z):

# '*' вместо ‘and’

print(x, y, z, w) # если F = 1

---

Смотрите также файлы

• А) отдельных категорий административных дел (разд. Iv.pdf

• Конспект содержания программы Инклюзивное и интегративное образование детей с овз в условиях введения и реализации фгос ноо овз.doc

• 13. 03. 02 Электроэнергетика и электротехника.docx

• Искусственный интеллект его возможности и потенциал.docx

• Анализ содержания организации и руководства игровой деятельности детей дошкольного возраста в режиме дня доо в группах детей раннего, младшего и старшего дошкольного возраста..docx