z1  ¬z2  ¬z3  ¬z4  z5

Сколько существует различных наборов значений переменных, при которых выражение ложно?

Решение:

1. 
   перепишем выражение, используя другие обозначения:
   

это выражение с пятью переменными, которые могут принимать 2⁵ = 32 различных комбинаций значений

2. 
   сначала определим число K комбинаций переменных, для которых выражение истинно; тогда число комбинаций, при которых оно ложно, вычислится как 32 – K
   
3. 
   заданное выражение истинно только тогда, когда истинно любое из двух слагаемых: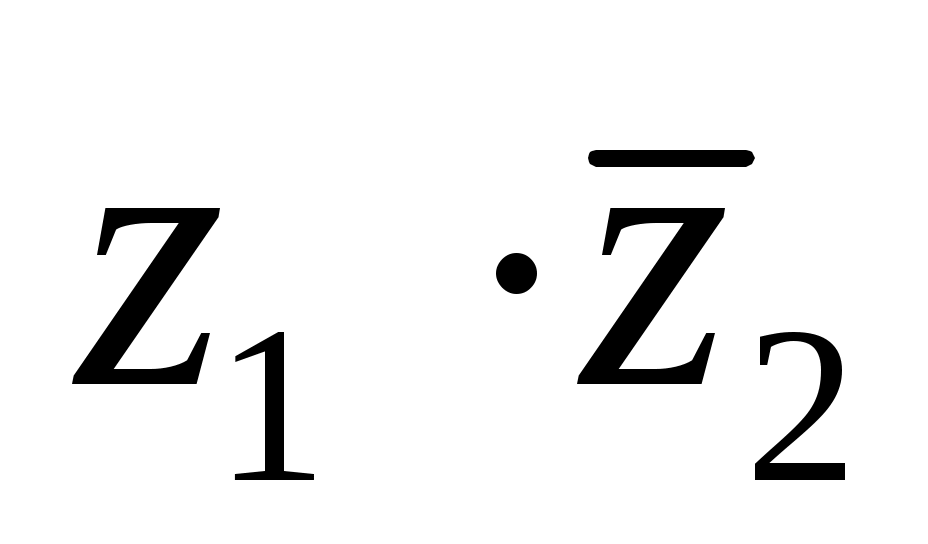 , 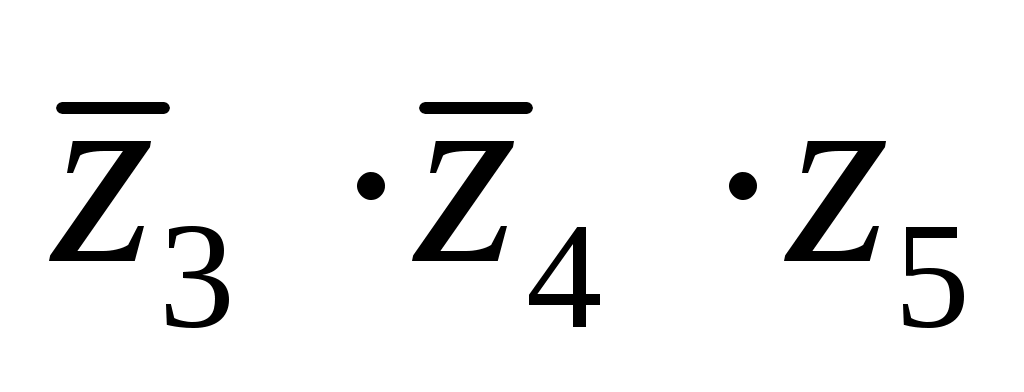или оба они истинны одновременно
   
4. 
   выражение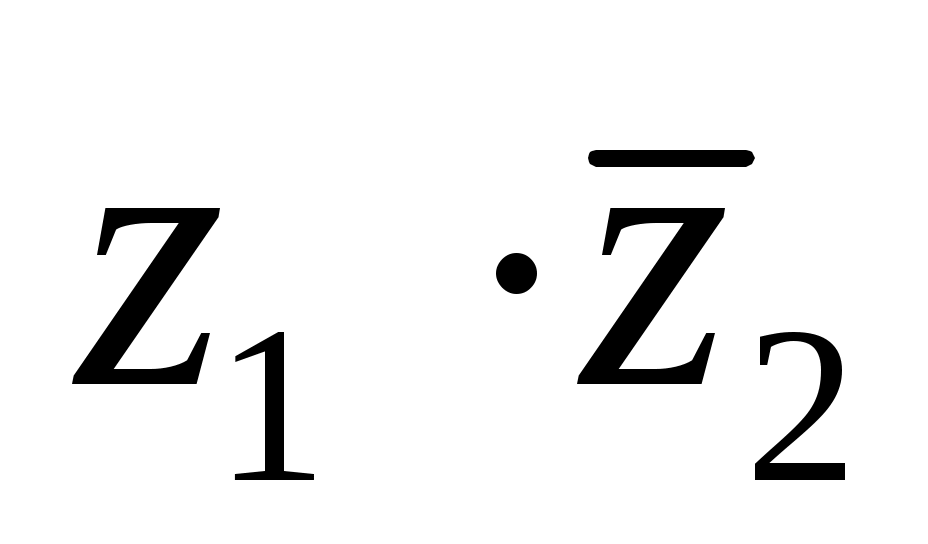 истинно только пр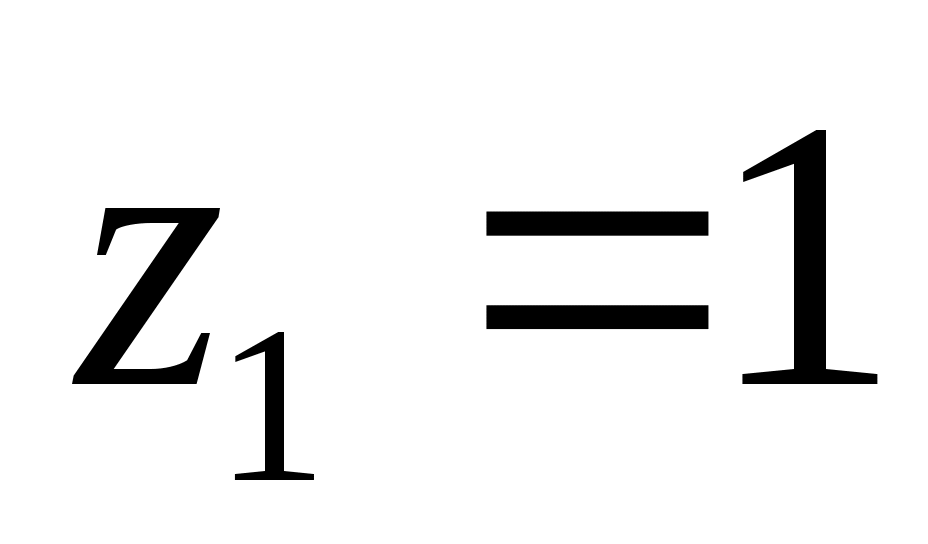и и 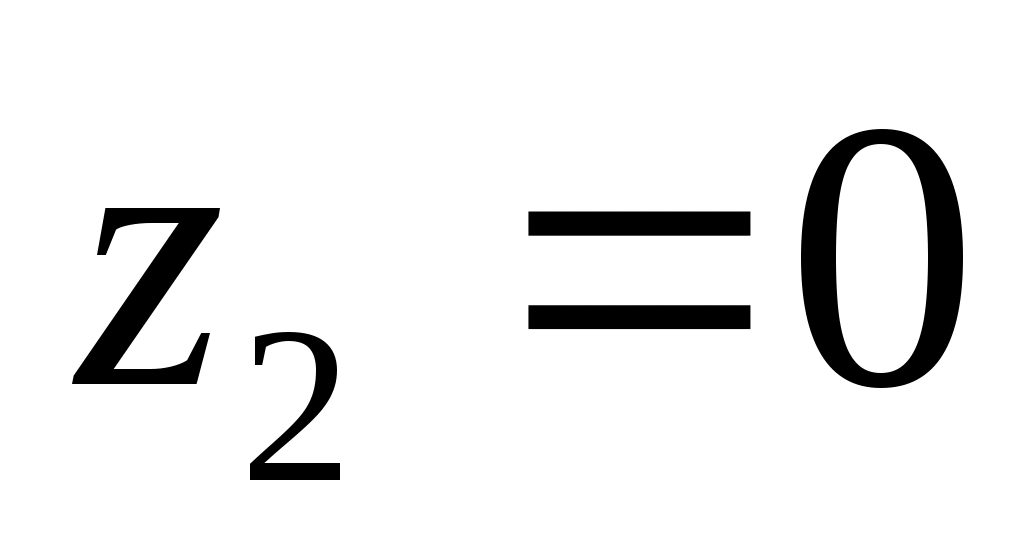, при этом остальные 3 переменных могут быть любыми, то есть, получаем всего 8 = 2³ вариантов
   
5. 
   выражение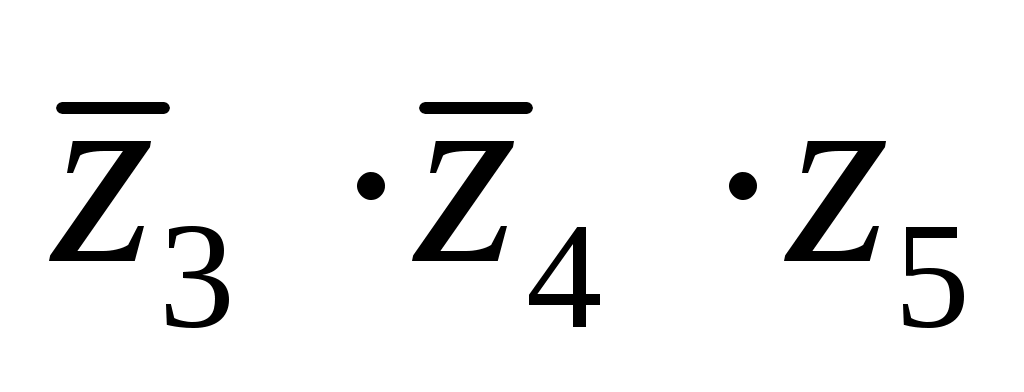 истинно только пр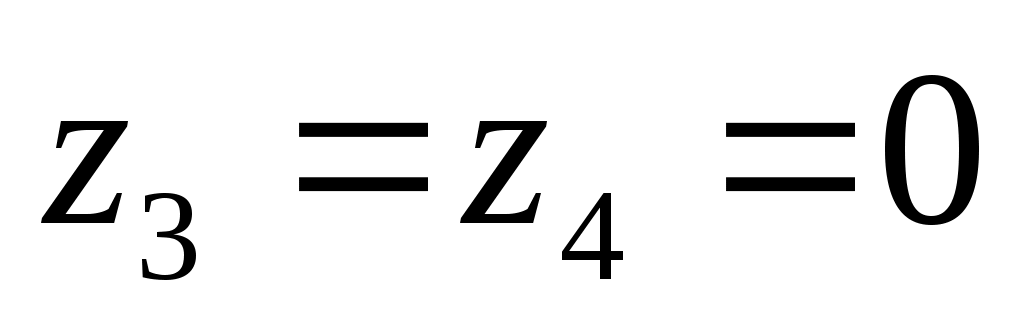и и 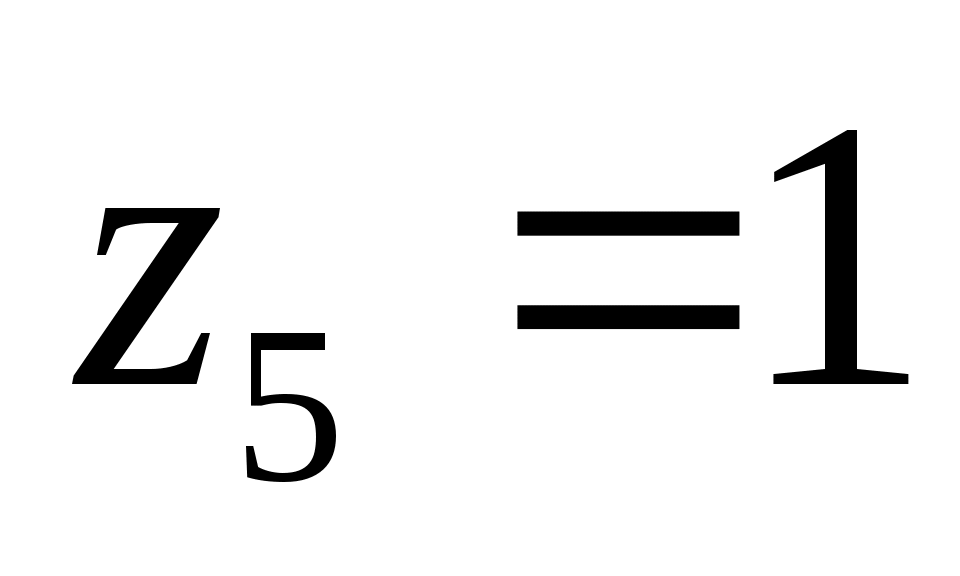, при этом остальные 2 переменных могут быть любыми, то есть, получаем всего 4 = 2² варианта
   
6. 
   заметим, что один случай, а именно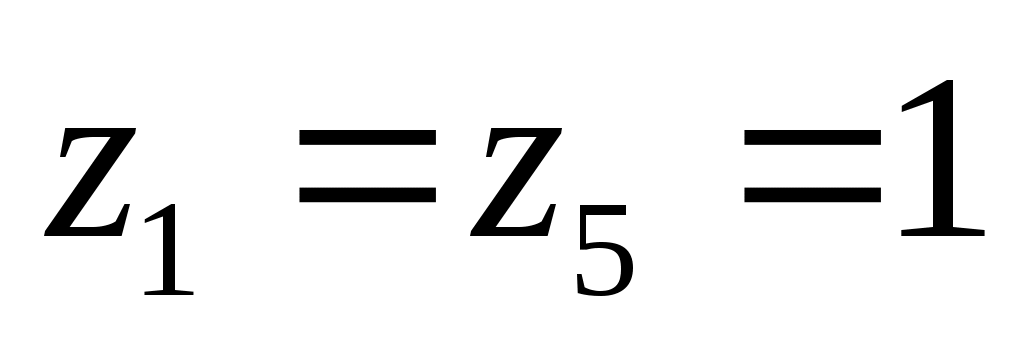 , 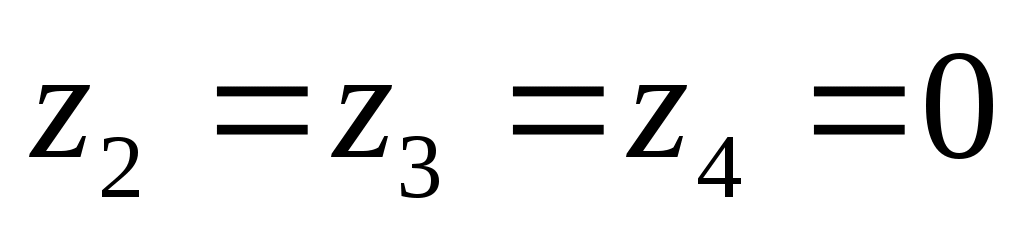обеспечивает истинность обоих слагаемых в исходном выражении, то есть, входит в обе группы (пп. 3 и 4), поэтому исходное выражение истинно для 11 = 8 + 4 – 1 наборов значений переменных, а ложно – для 32 – 11 = 21 набора.
   
7. 
   ответ: 21.
   

---

Ещё пример задания:

Р-04. Дан фрагмент таблицы истинности выражения F. Какое выражение соответствует F?

x1	x2	x3	x4	x5	x6	x7	F
0	1	0	1	1	1	0	0
1	1	0	1	0	1	0	1
0	1	0	1	1	0	1	0

1) (x1  x2)  ¬x3  x4  ¬x5  x6  ¬x7

2) (x1  x2)  ¬x3  x4  ¬x5  x6  x7

3) (x1  ¬x2)  x3  ¬x4  ¬x5  x6  ¬x7

4) (¬x1  ¬x2)  x3  ¬x4  x5  ¬x6  x7

Решение:

1. 
   в последнем столбце таблицы всего одна единица, поэтому стоит попробовать использовать функцию, состоящую из цепочки операций «И» (ответы 1, 3 или 4);
   
2. 
   для этой «единичной» строчки получаем, что инверсия (операция «НЕ») должна быть применена к переменным x_3, x₅ и x₇, которые равны нулю:
   

x1	x2	x3	x4	x5	x6	x7	F
1	1	0	1	0	1	0	1

---

таким образом, остается только вариант ответа 1 (в ответах 3 и 4 переменная x₃ указана без инверсии)

3. 
   проверяем скобку (x1  x2): в данном случае она равна 1, что соответствует условию
   
4. 
   ответ: 1.
   

Е

X	Y	Z	F
1	0	0	1
0	0	0	1
1	1	1	0

щё пример задания:

Р-03. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F. Какое выражение соответствует F?

1) ¬X  ¬Y  ¬Z 2) X  Y  Z 3) X  Y  Z 4) ¬X  ¬Y  ¬Z

Решение (основной вариант):

1. 
   нужно для каждой строчки подставить заданные значения X, Y и Z во все функции, заданные в ответах, и сравнить результаты с соответствующими значениями F для этих данных
   
2. 
   если для какой-нибудь комбинации X, Y и Z результат не совпадает с соответствующим значением F, оставшиеся строчки можно не рассматривать, поскольку для правильного ответа все три результата должны совпасть со значениями функции F
   
3. 
   перепишем ответы в других обозначениях:
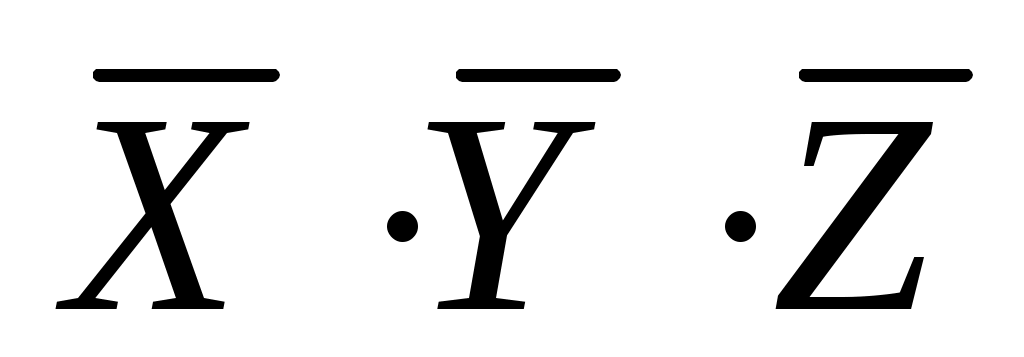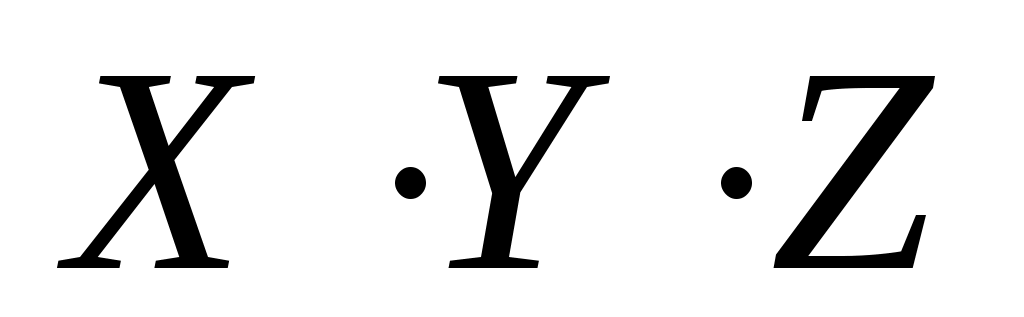   1) 2) 3) 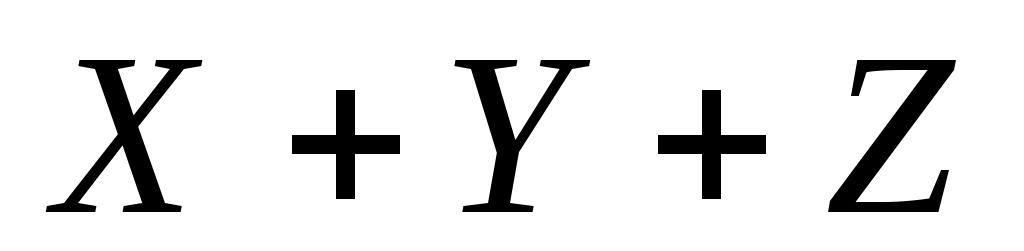4)
   
4. 
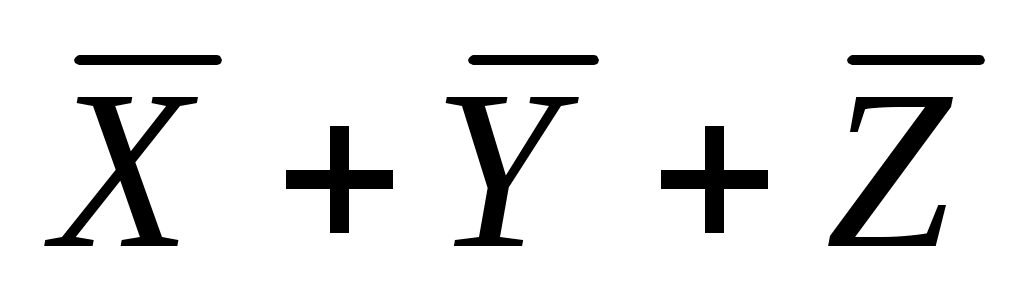
   первое выражение,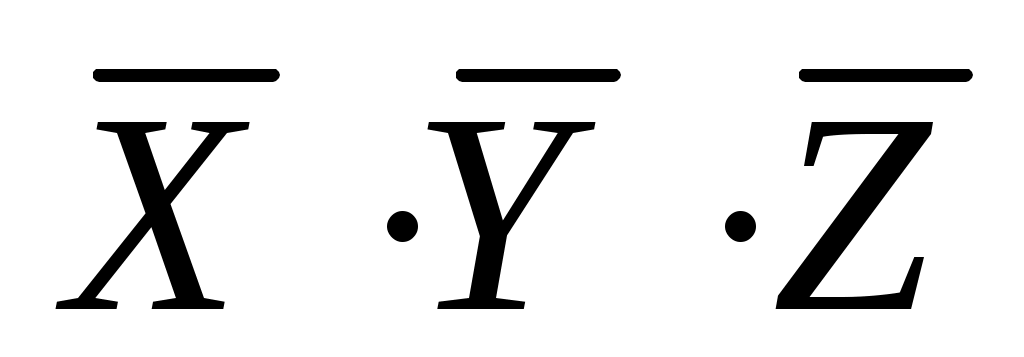 , равно 1 только при 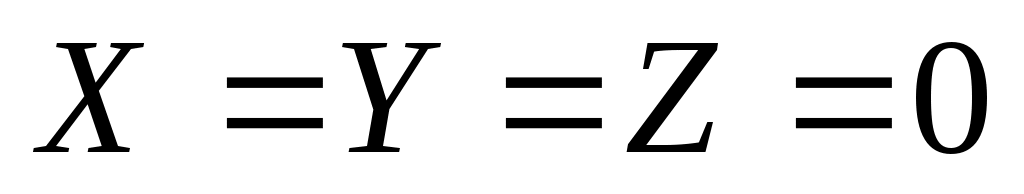, поэтому это неверный ответ (первая строка таблицы не подходит)
   
5. 
   второе выражение,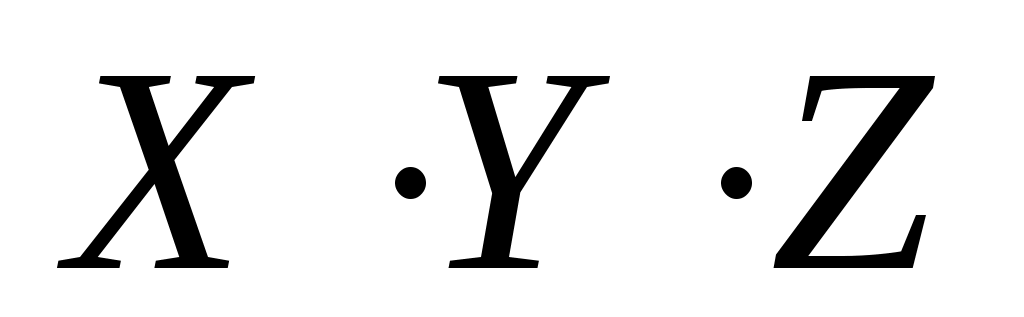 , равно 1 только при 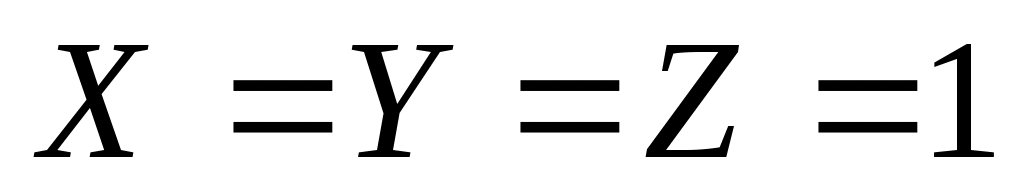, поэтому это неверный ответ (первая и вторая строки таблицы не подходят)
   
6. 
   третье выражение,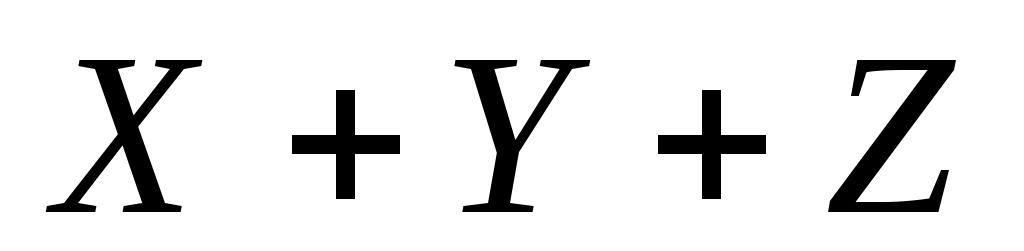 , равно нулю при 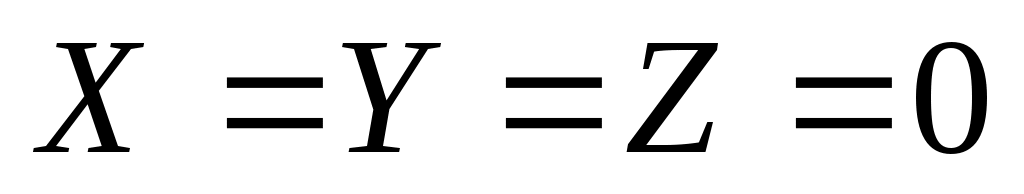, поэтому это неверный ответ (вторая строка таблицы не подходит)
   
7. 
   наконец, четвертое выражение,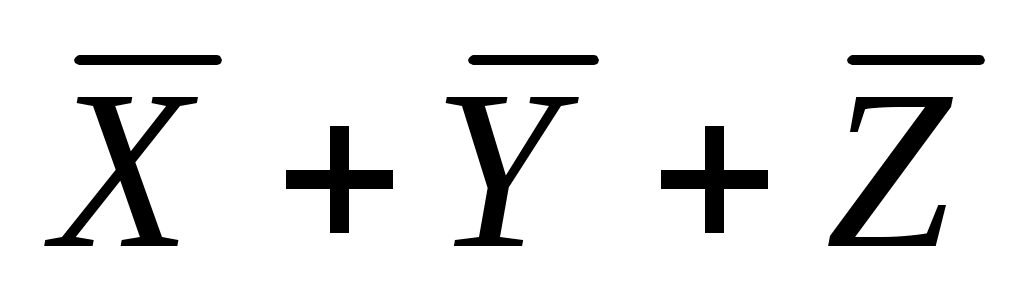 равно нулю только тогда, когда 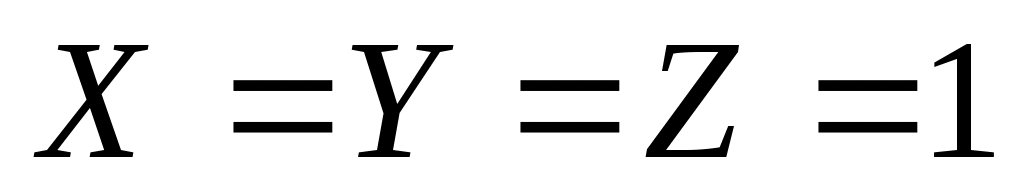, а в остальных случаях равно 1, что совпадает с приведенной частью таблицы истинности
   
8. 
   таким образом, правильный ответ – 4 ; частичная таблица истинности для всех выражений имеет следующий вид:
   

---

X	Y	Z	F
1	0	0	1	0 ×	0 ×	1	1
0	0	0	1	–	–	0 ×	1
1	1	1	0	–	–	–	0

(красный крестик показывает, что значение функции не совпадает с F, а знак «–» означает, что вычислять оставшиеся значения не обязательно).

Возможные ловушки и проблемы: серьезные сложности представляет применяемая в заданиях ЕГЭ форма записи логических выражений с «закорючками», поэтому рекомендуется сначала внимательно перевести их в «удобоваримый» вид; расчет на то, что ученик перепутает значки  и  (неверный ответ 1) в некоторых случаях заданные выражения-ответы лучше сначала упростить, особенно если они содержат импликацию или инверсию сложных выражений (как упрощать – см. разбор задачи А10)

Решение (вариант 2):

1. 
   часто правильный ответ – это самая простая функция, удовлетворяющая частичной таблице истинности, то есть, имеющая единственный нуль или единственную единицу в полной таблице истинности
   
2. 
   в этом случае можно найти такую функцию и проверить, есть ли она среди данных ответов
   
3. 
   в приведенной задаче в столбце F есть единственный нуль для комбинации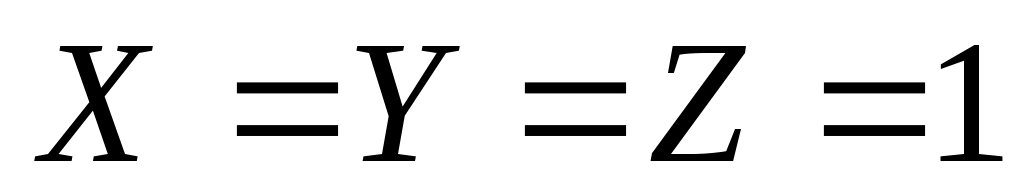
   
4. 
   выражение, которое имеет единственный нуль для этой комбинации, это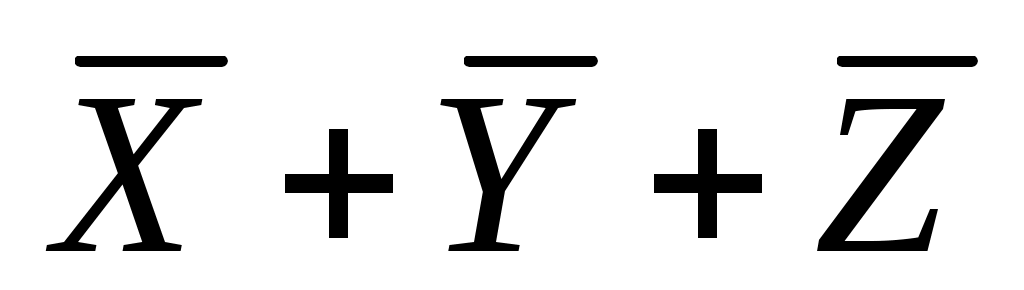 , оно есть среди приведенных ответов (ответ 4)
   
5. 
   таким образом, правильный ответ – 4
   

---

Возможные проблемы: метод применим не всегда, то есть, найденная в п. 4 функция может отсутствовать среди ответов

---

Смотрите также файлы

• А) отдельных категорий административных дел (разд. Iv.pdf

• Конспект содержания программы Инклюзивное и интегративное образование детей с овз в условиях введения и реализации фгос ноо овз.doc

• 13. 03. 02 Электроэнергетика и электротехника.docx

• Искусственный интеллект его возможности и потенциал.docx

• Анализ содержания организации и руководства игровой деятельности детей дошкольного возраста в режиме дня доо в группах детей раннего, младшего и старшего дошкольного возраста..docx