Файл: Основные задания к самостоятельным работам в системе gpss.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Решение задач

Дисциплина: Не указана

Добавлен: 09.11.2023

Просмотров: 77

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


Можно отметить, как с ростом продолжительности периода моделирования вероятности переходов становятся все ближе к заявленным исходным вероятностям: если по истечении 10000 единиц времени максимальное отклонение от заданной вероятности составляло 0,051, то по истечении 70000 единиц времени, максимальное отклонение уже равняется только 0,006.
Вариант 3.2.3. Предыдущие варианты можно выполнить, заменив блок TRANSFER на блок FUNCTION.

Программа:
GRUP FUNCTION RN777,D5 ;задаем функцию

0.1,11/0.3,12/0.6,13/0.75,14/1.0,15

MKU12 EQU 12 ;объявляем номер МКУ

MKU12 STORAGE 2 ;и число каналов в нем

MKU13 EQU 13

MKU13 STORAGE 2

MKU14 EQU 14

MKU14 STORAGE 2

MKU15 EQU 15

MKU15 STORAGE 2

SIMULATE

GENERATE (Exponential(1,0,10)),,,,1 ;поступление заявок с приоритетом

QUEUE OCH1 ;стали в очередь

SEIZE OKU1 ;заняли прибор

DEPART OCH1 ;ушли из очереди

ADVANCE (Exponential(2,0,8)) ;обслуживание

RELEASE OKU1 ;освободили прибор

ASSIGN 1,FN$GRUP ;пишем в 1-й параметр номер

nxt TEST E P1,11,nxt1 ;отдельно выделяем тех, кто вернется на ОКУ1

PRIORITY 0 ;убираем приоритет

prb1 QUEUE OCH2 ;стали в очередь

SEIZE OKU1 ;заняли прибор

DEPART OCH2 ;ушли из очереди

ADVANCE (Exponential(3,0,8)) ;обслуживание

RELEASE OKU1 ;освободили прибор

TERMINATE ;покинули систему

nxt1 QUEUE P1 ;стали в очередь

ENTER P1 ;заняли канал

DEPART P1 ;ушли из очереди

ADVANCE (Exponential(4,0,50)) ;обслуживание

LEAVE P1 ;освободили канал

TERMINATE ;покинули систему

GENERATE 10000 ;время моделирования

SAVEVALUE Prob1,(N$prb1/N$nxt) ;вычисляем вероятность перехода

SAVEVALUE Prob2,(QC12/N$nxt) ;вычисляем вероятность перехода

SAVEVALUE Prob3,(QC13/N$nxt) ;с помощью чисел входа в очередь

SAVEVALUE Prob4,(QC14/N$nxt)

SAVEVALUE Prob5,(QC15/N$nxt)

TERMINATE 1

START 1
Файл REPORT:

START TIME END TIME BLOCKS FACILITIES STORAGES

0.000 10000.000 28 1 4

NAME VALUE

GRUP 10000.000

MKU12 12.000

MKU13 13.000

MKU14 14.000

MKU15 15.000

NXT 8.000

NXT1 16.000

OCH1 10005.000

OCH2 10007.000

OKU1 10006.000

PRB1 10.000

PROB1 10008.000

PROB2 10009.000

PROB3 10010.000

PROB4 10011.000

PROB5 10012.000

LABEL LOC BLOCK TYPE ENTRY COUNT CURRENT COUNT RETRY

1 GENERATE 983 0 0

2 QUEUE 983 1 0

3 SEIZE 982 0 0

4 DEPART 982 0 0

5 ADVANCE 982 0 0

6 RELEASE 982 0 0

7 ASSIGN 982 0 0

NXT 8 TEST 982 0 0

9 PRIORITY 93 0 0

PRB1 10 QUEUE 93 16 0

11 SEIZE 77 0 0

12 DEPART 77 0 0

13 ADVANCE 77 1 0

14 RELEASE 76 0 0

15 TERMINATE 76 0 0

NXT1 16 QUEUE 889 13 0

17 ENTER 876 0 0

18 DEPART 876 0 0

19 ADVANCE 876 7 0

20 LEAVE 869 0 0

21 TERMINATE 869 0 0

22 GENERATE 1 0 0

23 SAVEVALUE 1 0 0

24 SAVEVALUE 1 0 0

25 SAVEVALUE 1 0 0

26 SAVEVALUE 1 0 0

27 SAVEVALUE 1 0 0

28 TERMINATE 1 0 0

FACILITY ENTRIES UTIL. AVE. TIME AVAIL. OWNER PEND INTER RETRY DELAY

OKU1 1059 0.883 8.337 1 844 0 0 0 17

QUEUE MAX CONT. ENTRY ENTRY(0) AVE.CONT. AVE.TIME AVE.(-0) RETRY


12 5 2 218 161 0.243 11.133 42.578 0

13 14 11 303 81 2.200 72.596 99.083 0

14 2 0 119 99 0.050 4.207 25.029 0

15 12 0 249 130 0.961 38.608 80.785 0

OCH1 17 1 983 111 3.137 31.911 35.973 0

OCH2 18 16 93 6 2.421 260.364 278.320 0

STORAGE CAP. REM. MIN. MAX. ENTRIES AVL. AVE.C. UTIL. RETRY DELAY

MKU12 2 0 0 2 216 1 0.911 0.456 0 2

MKU13 2 0 0 2 292 1 1.612 0.806 0 11

MKU14 2 1 0 2 119 1 0.646 0.323 0 0

MKU15 2 0 0 2 249 1 1.233 0.617 0 0

SAVEVALUE RETRY VALUE

PROB1 0 0.095

PROB2 0 0.222

PROB3 0 0.309

PROB4 0 0.121

PROB5 0 0.254

FEC XN PRI BDT ASSEM CURRENT NEXT PARAMETER VALUE

844 0 10001.196 844 13 14 1 11.000

972 1 10015.941 972 19 20 1 15.000

985 1 10016.916 985 0 1

928 1 10045.509 928 19 20 1 13.000

981 1 10046.165 981 19 20 1 12.000

979 1 10057.562 979 19 20 1 12.000

971 1 10075.759 971 19 20 1 14.000

978 1 10083.442 978 19 20 1 15.000

935 1 10150.839 935 19 20 1 13.000

986 0 20000.000 986 0 22

Преимуществом задания вероятности перехода с помощью функцию в сравнении с блоком TRANSFER является то, что с помощью функции можно реализовать большое число разных переходов в несколько строк модели, тогда как если делать это же самое с помощью блока TRANSFER, нам для каждого перехода необходимо предварительно вычислить все вероятности с учетом тех потоков, которые уже были отсечены предыдущими блоками TRANSFER.

Также, как и в предыдущей модели, проведем несколько экспериментов с различным временем моделирования с целью выявления зависимость погрешности реализации разветвлений от времени моделирования
10000
20000
30000
40000
50000
60000
70000



0,095
0,093
0,094
0,098
0,102
0,103
0,103



0,222
0,205
0,204
0,201
0,199
0,198
0,197



0,309
0,325
0,316
0,315
0,308
0,309
0,307



0,121
0,130
0,137
0,138
0,141
0,141
0,145



0,254
0,247
0,249
0,248
0,250
0,249
0,249


Как видим, результаты несколько отличаются от тех, что были получены при использовании блоков TRANSFER, но сама тенденция остается неизменной – при росте продолжительности моделирования вероятности переходов становятся все ближе к заявленным исходным вероятностям

4. ЗАДАНИЕ на тему: сравнение результатов математического и имитационного моделирования на примерах моделирования АвтоЗаправочных Станций (АЗС).

Вариант
13

L - Частота появления АМ на АЗС, в 1 мин.
5

N - Количество работающих БК на АЗС
4

Тобсл. - Длительность заправки, мин
5

Ro - Ограничение длины очереди АМ к АЗС
5

Получаем:

Система обслуживания (СМО) представляет собой автозаправку (АЗ) с 4 бензоколонками (БК), к которой подъезжают автомобили (АМ) с частотой 5 АМ в минуту и, если нет очереди, то сразу подъезжают к одной из свободных БК для заправки, которая длится в среднем Tобсл = 5 минут. При наличии очереди в 5 машин АМ покидает АЗ.

Пункты задания:

1. Построить схему СМО, по ней построить граф состояний.





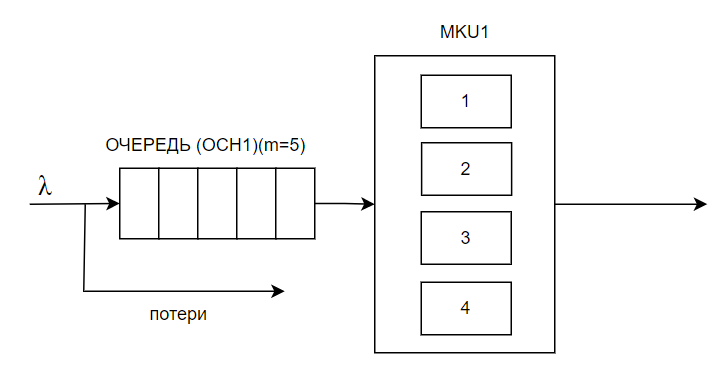
Система: М/М/4/5

Состояния системы:

  1. S0 – в системе нет заявок (все каналы свободны)

  2. S1 – занят один канал, остальные свободны

  3. S2 – занят второй канал, остальные свободны

  4. S3 – занят третий канал, остальные свободны

  5. S4 – занят четвертый канал, остальные свободны

  6. S5 – заняты все 4 канала + 1 в очереди заявки

  7. S6 – заняты все 4 канала, + 2 в очереди заявки

  8. S7 – заняты все 4 канала, + 3 в очереди заявки

  9. S8 – заняты все 4 канала, + 4 в очереди заявки

  10. S9 – заняты все 4 канала, + 5 в очереди заявки

2. Определить, к какой группе типовых схем СМО относится заданная система обслуживания, записать формулы расчета основных характеристик этой СМО и выполнить вычисления значений этих характеристик.


В данном случае перед нами многоканальная СМО с ограниченной длиной очереди = 4.

Показатель интенсивности поступления заявок:



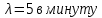
Интенсивность обслуживания:

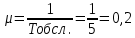
Определим показатели работы. Вычислим нагрузку на СМО:



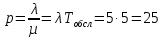
Далее находим:

- вероятность простоя системы (отсутствие машин на АЗС):



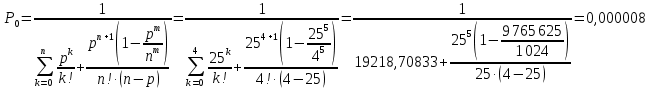
Время простоя = Tпр =

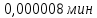
занят 1 канал:

P1 = 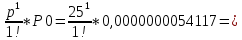0,0000001353

заняты 2 канала:

P2 = 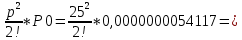0,0000016911

заняты 3 канала:

P3 = 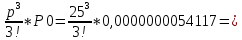0,0000140929

заняты 4 канала:

P4 = 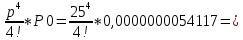0,0000880805

При появлении очереди, рассчитывается по след. формуле:



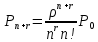
Заняты 4 канала + 1 в очереди:

P5 = 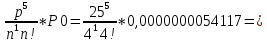0,00055050287

Заняты 4 канала + 2 в очереди:

P6 = 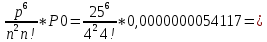0,00344064293

Заняты 4 канала + 3 в очереди:

P7 = 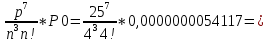0,02150401833

Заняты 4 канала + 4 в очереди:

P8 = 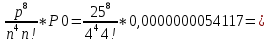0,13440011458

Заняты 4 канала + 5 в очереди:

P9 = 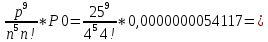0,84000071611

Чтобы проверить правильность нахождения, необходимо сложить их, должны получить 1:



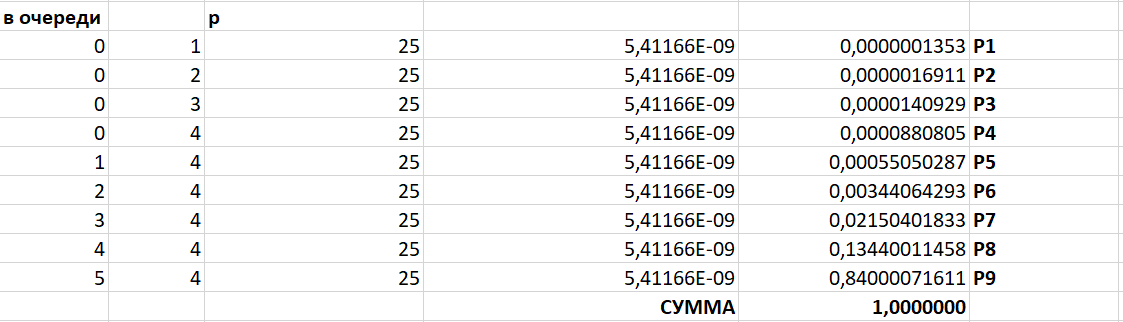
Сумма = 1, следовательно вероятность найдена правильно.

Вероятность отказа - доля заявок, получивших отказ

Pотк = P6 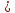0,84000071611

Значит, 84% из числа поступивших заявок не принимаются к обслуживанию.

Вероятность обслуживания поступающих заявок

Pобс = 1 - Pотк = 1 – 0,84 = 0,16

Среднее число каналов, занятых обслуживанием

Nз = ρ*Pобс = 25*0,16 = 4 канала, то есть практически всегда все 4 канала заняты

Смотрите также файлы