Файл: Экзаменационные вопросы по общественному здоровью и здравоохранению.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 439
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Клинико-статистическое исследование - использование статистических методов при обработке результатов клинических, экспериментальных и лабораторных исследований; позволяет с количественной точки зрения оценить достоверность результатов исследования и решить ряд других задач.
Особенности клинико-статистического исследования:
а) выборочное исследование
б) выборка малая
в) результаты обрабатываются не параметрическими методами исследования
г) наличие всегда конкретной группы либо копии (паракопии)
д) единица наблюдения чаще всего - пациент
76. Относительные величины, виды, методы расчета. Использование в работе врача. Возможные ошибки в применении относительных величин.
Относительные величины (показатели, коэффициенты) получаются в результате отношения одной абсолютной величины к другой. Наиболее часто используются следующие показатели:
а) интенсивные - показатели частоты, интенсивности, распространенности явления в среде, продуцирующей данное явление.
В здравоохранении изучаются заболеваемость, смертность, инвалидность, рождаемость и другие показатели здоровья населения. Средой, в которой происходят процессы, является население в целом или его отдельные группы (возрастные, половые, социальные, профессиональные и др.). В медико-статистических исследованиях явление представляет собой как бы продукт среды. Например, население (среда) и заболевшие (явление); больные (среда) и умершие (явление) и т. д.
Величина основания выбирается в соответствии в величиной показателя - на 100, 1000, 10000, 100000, в зависимости от этого показатель выражается в процентах, промилле, продецимилле,просантимилле.
Интенсивные показатели могут быть
1. общими - характеризуют явление в целом (общие показатели рождаемости, смертности, заболеваемости, вычисленные ко всему населению административной территории)
2. специальными (погрупповыми)
- применяются для характеристики частоты явления в различных группах ( заболеваемость по полу, возрасту, смертность среди детей в возрасте до 1 года, летальность по отдельным нозологическим формам и т.д.)
Интенсивные показатели применяются в медицине:
- для определения уровня, частоты, распространенности явления
- для сравнения частоты явления в двух различных совокупностях
- для изучения изменений частоты явления в динамике.
б) экстенсивные - показатели удельного веса, структуры, характеризуют распределение явления на составные части, его внутреннюю структуру. Вычисляются экстенсивные показатели отношением части явления к целому и выражаются в процентах или долях единицы.
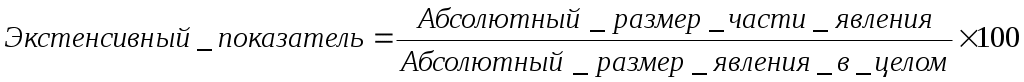
Экстенсивные показатели используются для определения структуры явления и сравнительной оценки соотношения составляющих его частей. Экстенсивные показатели всегда взаимосвязаны между собой, т. к. их сумма всегда равна 100 процентам: так, при изучении структуры заболеваемости удельный вес отдельного заболевания может возрасти:
- при истинном росте числа заболеваний
- при одном и том же его уровне, если число других заболеваний снизилось
- при снижении числа данного заболевания, если уменьшение числа других заболеваний происходит более быстрыми темпами.
При анализе экстенсивный показатель следует применять с осторожностью и помнить, что им пользуются только для характеристики состава (структуры) явления в данный момент времени и в данном месте.
Примеры использования в работе врача: лейкоцитарная формула; структура населения по полу, возрасту, социальному положению; структура заболеваний по нозологии; структура причин смерти.
в) соотношения - представляют собой соотношение двух самостоятельных, независимых друг от друга, качественно разнородных величи, сопоставляемых только логически.
Примеры использования в работе врача: показатели обеспеченности населения врачами, больничными койками; показатели, отражающие число лабораторных исследований на 1 врача и т.д.
г) наглядности - применяются с целью более наглядного и доступного сравнения статистических величин. Показатели наглядности представляют удобный способ преобразования абсолютных, относительных или средних величин в легкую для сравнения форму. При вычислении этих показателей одна из сравниваемых величин приравнивается к 100 (или 1), а остальные величины пересчитываются соответственно этому числу.
Показатели наглядности указывают, на сколько процентов или во сколько раз произошло увеличение или уменьшение сравниваемых величин. Показатели наглядности используются чаше всего для сравнения данных в динамике, чтобы представить закономерности изучаемого явления в более наглядной форме.
При пользовании относительными величинами могут быть допущены некоторые ошибки:
1. иногда судят об изменении частоты явления на основе экстенсивных показателей, которые характеризуют структуру явления, а не его интенсивность.
2. нельзя складывать и вычитать статистические показатели, которые рассчитаны из совокупностей, имеющих разную численность, ибо это приводит к грубым искажениям показателя.
3. при расчете специальных показателей следует правильно выбирать знаменатель для расчета показателя: например, показатель послеоперационной летальности необходимо рассчитывать по отношению к оперированным, а не всем больным.
4. при анализе показателей следует учитывать фактор времени: нельзя сравнивать между собой показатели, вычисленные за различные периоды времени (показатель заболеваемости за год и за полугодие), что может привести к ошибочным суждениям.
5. нельзя сравнивать между собой общие интенсивные показатели, вычисленные из неоднородных по составу совокупностей, поскольку неоднородность состава среды может влиять на величину интенсивного показателя.
77. Интенсивные и экстенсивные показатели. Методика расчета, единицы измерения, использование в работе учреждений здравоохранения.
См. вопрос 76
78. Показатели соотношения и наглядности. Методика расчета, единицы измерения, применение в здравоохранении.
См. вопрос 76.
79. Вариационный ряд, его элементы, виды, правила построения
См. вопрос 80.
80. Средние величины, виды, методика расчета. Применение в работе врача.
Средние величины дают обобщающую характеристику статистической совокупности по определенному изменяющемуся количественному признаку. Средняя величина характеризует весь ряд наблюдений одним числом, выражающим общую меру изучаемого признака. Она нивелирует случайные отклонения отдельных наблюдений и дает типичную характеристику количественного признака.
Требования к средним величинам:
1) качественная однородность совокупности, для которой рассчитывается средняя величина - только тогда
она будет объективно отображать характерные особенности изучаемого явления.
2) средняя величина должна основываться на массовом обобщении изучаемого признака, т.к. только тогда она выражает типичные размеры признака
Средние величины получаются из рядов распределения (вариационных рядов).
Вариационный ряд- ряд однородных статистических величин, характеризующих один и тот же количественный учетный признак, отличающихся друг от друга по своей величине и расположенных в определенном порядке (убывания или возрастания).
Элементы вариационного ряда:
а) варианта - v - числовое значение изучаемого меняющегося количественного признака.
б) частота - p (pars) или f (frequency) - повторяемость вариант в вариационном ряду, показывающая, как часто встречается та или иная варианта в составе данного ряда.
в) общее число наблюдений- n (numerus) - сумма всех частот: n=ΣΡ. Если общее число наблюдений более 30,статистическая выборка считается большой, если n меньше или равно 30 - малой.
Вариационные ряды бывают:
1. в зависимости от значения варианты:
а) прерывные (дискретные), состоящие из целых чисел
б) непрерывные, когда значения вариант выражены дробным числом. В прерывных рядах смежные варианты отличаются друг от друга на целое число (число ударов пульса, число дыханий в минуту, число дней лечения). В непрерывных рядах варианты могут отличаться на любые дробные значения единицы.
2. в зависимости от частоты встречаемости признака:
а) простой - ряд - каждая варианта встречается один раз, т.е. частоты равны единице.
б) обычный - ряд, в котором варианты встречаются более одного раза.
в) сгруппированный- ряд, в котором варианты объединены в группы по их величине в пределах определенного интервала с указанием частоты повторяемости всех вариант, входящих в группу.
Сгруппированный вариационный ряд используют при большом числе наблюдений и больном размахе крайних значений вариант.
Обработка вариационного ряда заключается в получении параметров вариационного ряда (средней величины, среднего квадратического отклонения и средней ошибки средней величины).
3. в зависимости от числа наблюдений:
а) четные и нечетные
б) большой (при числе наблюдений больше 30) и малый (если число наблюдений меньше или равно 30)
Виды средних величин:
а) мода (Мо) - величина признака, чаще других встречающаяся в совокупности. За моду принимают варианту, которой соответствует наибольшее количество частот вариационного ряда.
б) Медиана (Me) - величина признака, занимающая срединное значение в вариационном ряду. Она делит вариационный ряд на две равные части.
На величину моды и медианы не оказывают влияния числовые значения крайних вариант, имеющихся в вариационном ряду. Они не всегда могут точно характеризовать вариационный ряд и применяются в медицинской статистике относительно редко. Более точно характеризует вариационный ряд средняя арифметическая величина.
в) Средняя арифметическая(М, или
) - рассчитывается на основе всех числовых значений изучаемого признака.Реже применяются другие средние величины: средняя геометрическая (при обработке результатов титрования антител, токсинов, вакцин); средняя квадратическая (при определении среднего диаметра среза клеток, результатов накожных иммунологических проб); средняя кубическая (для определения среднего объема опухолей) и другие.
В простом вариационном ряду, где варианты встречаются только по одному разу, вычисляется средняя арифметическая простая по формуле:
, где V - числовые значения вариант, n - число наблюдений, Σ - знак суммыВ обычном вариационном ряду вычисляется средняя арифметическая взвешенная по формуле:
, где V - числовые значения вариант, р - частота встречаемости вариант, n - число наблюдений.Средние величины являются важными обобщающими характеристиками совокупности. Однако за ними скрываются индивидуальные значения признака. Средние величины не показывают изменчивости, колеблемости признака. Если вариационный ряд более компактен, менее рассеян и все отдельные значения расположены вокруг средней, то средняя величина дает более точную характеристику данной совокупности. Если вариационный ряд растянут, отдельные значения значительно отклоняются от средней, т.е. имеется большая вариабельность количественного признака, то средняя менее типична, хуже отражает в целом весь ряд.