Файл: Экзаменационные вопросы по общественному здоровью и здравоохранению.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 414
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Мвыб- средняя величина, полученная при проведении исследования на выборочной совокупности; t - доверительный коэффициент, значение которого определяется степенью вероятности безошибочного прогноза, с которой исследователь желает получить результат; mM - ошибка репрезентативности средней величины.
2) для относительных величин:
, где Рген - доверительные границы относительной величины в генеральной совокупности; Рвыб- относительная величина, полученная при проведении исследования на выборочной совокупности; t - доверительный коэффициент; mP - ошибка репрезентативности относительной величины.Доверительные границы показывают, в каких пределах может колебаться размер выборочного показателя в зависимости от причин случайного характера.
При малом числе наблюдений (n<30), для вычисления доверительных границ значение коэффициента t находят по специальной таблице Стьюдента. Значения t расположены в таблице на пересечении с избранной вероятностью безошибочного прогноза и строки, указывающей на имеющееся число степеней свободы (n), которое равно n-1.
84. Оценка достоверности различий относительных и средних величин. Понятие о критерии «t»
При проведении медико-биологических исследований на двух сравниваемых совокупностях возникает необходимость определить не только их различие, но и его достоверность. Метод оценки достоверности разности показателей или средних величин позволяет установить, существенны ли выявленные различия, или они являются результатом действия случайных причин.
В основе метода лежит определение критерия достоверности "t", который рассчитывается по специальным формулам для средних и относительных величин:
для средних:
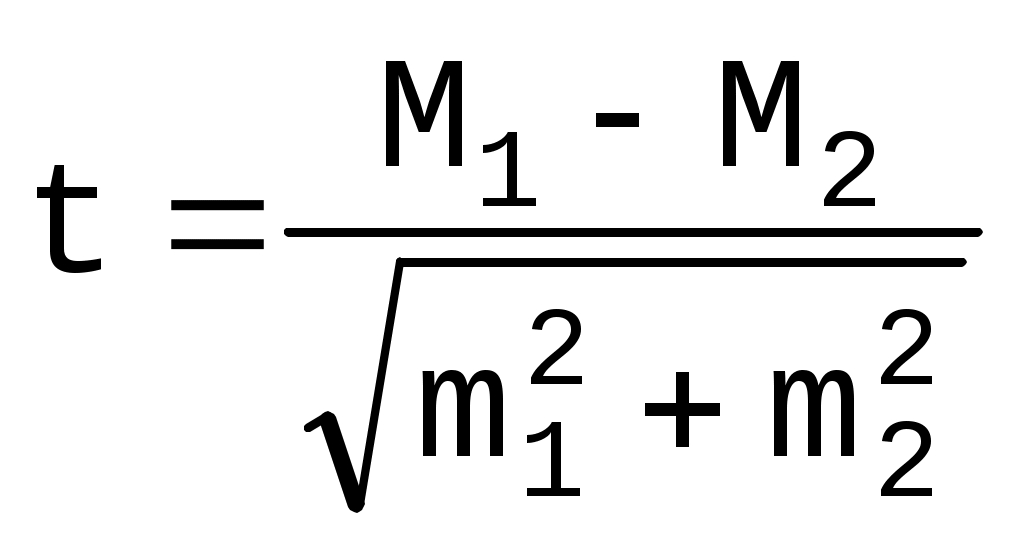, а для относительных величин 
, где Μ1, Μ2, P1 и P2 - статистические величины, полученные при проведении выборочных исследований: m1 и m2 - их ошибки репрезентативности; t - коэффициент достоверности.
При большой выборке различие достоверно при t>2, что соответствует вероятности безошибочного прогноза равной или более 95%. При величине коэффициента достоверности t<2 степень вероятности безошибочного прогноза менее 95%. При такой степени вероятности мы не можем утверждать, что полученная разность показателей достоверна с достаточной степенью вероятности. В этом случае необходимо получить дополнительные данные, увеличив число наблюдений. Если после увеличения численности выборки, и, соответственно, уменьшения ошибки репрезентативности, различие продолжает оставаться недостоверным, можно считать доказанным, что между сравниваемыми совокупностями не обнаружено различий по изучаемому признаку.
Для определения достоверности различий между двумя показателями или средними величинами при малом числе наблюдений критерий достоверности оценивается по таблице значений критерия t Стьюдента по числу степеней свободы, которое при этом определяется как сумма чисел наблюдений в каждой группе без двух.
85. Графические изображения в статистике. Виды диаграмм, правила их построения и оформления.
Результаты статистического исследования могут быть представлены в виде графических изображений, что позволяет более наглядно продемонстрировать полученные результаты и облегчает проведение анализа.
Существует несколько видов графических изображений, наиболее часто используют диаграммы (линейные, радиальные, столбиковые, ленточные, гистограммы, секторные и др.), картограммы, картодиаграммы.
При построении графических изображений необходимо соблюдать следующие правила:
- данные на графике должны размещаться слева направо и снизу вверх;
- обязательное условие при построении графика - соблюдение масштабности;
- нулевые точки шкал при наличии возможности должны быть изображены на диаграмме
- цифры, показывающие деление шкал, помещаются слева или внизу соответствующей шкалы;
- линии, представляющие диаграмму изображаемого явления, следует делать иного вида, нежели вспомогательные линии;
- на кривой, отражающей динамику явления, необходимо отметить все точки, соответствующие отдельным наблюдениям;
- в диаграммах, показывающих структуру, должна быть оттенена как линия нулевая
, так и 100-процентная;
- изображенные графические величины должны иметь цифровые обозначения на самом графике или в прилагаемой к нему таблице;
- символы, используемые при построении диаграммы (цвет, штриховка, фигуры, знаки), должны быть пояснены;
- каждый график должен иметь четкое, краткое название, отражающее его содержание;
- название диаграммы должно размешаться под рисунком.
Виды диаграмм:
а) линейные диаграммы - позволяют изображать динамику явления (изменение показателей во времени). Линейная диаграмма строится в системе прямоугольных координат, при ее построении следует учитывать соотношение между основанием и высотой - абсциссой х и ординатой у, основанное на принципе "золотого сечения": это соотношение должно быть 1,6:1. На горизонтальной оси (оси абсцисс) откладываются отрезки, обозначающие периоды времени. На вертикальной оси (оси ординат) откладываются размеры изучаемого явления. Обязательное условие при построении графика - масштабность. На одной диаграмме можно изобразить несколько линий, отличающихся друг от друга цветом, толщиной или формой пунктира.
б) радиальные диаграммы (диаграммы полярных координат, линейно-круговые диаграммы, векторные диаграммы) - применяются для изображения сезонных (подекадных, помесячных, поквартальных) и других колебаний, имеющих замкнутый, циклический характер (за сутки, неделю и т.д.). Для их построения круг делится на столько секторов, на сколько частей разделен период времени, взятый для изучения явления (например, на 12 - при изучении помесячных колебаний в течение года; на 7 - при изучении явления за неделю). На каждом из радиусов с соблюдением масштабности отмечаются показатели, полученные точки соединяют прямыми линиями. Начало маркировки радиусов начинается с радиуса, соответствующего нулю градусов, и продолжается по часовой стрелке.
в) столбиковые диаграммы - строятся по такому же принципу, как и линейные, в системе координат, с соблюдением масштабности, но в которых вертикально или горизонтально проводимым линиям соответствуют прямоугольники. Эти диаграммы используются для изображения сравнительной величины явления в какой-либо определенный промежуток времени, например, сравнительной численности населения по странам мира; обеспеченности населения врачами в разные годы и т.д.
г) гистограммы - в виде прямоугольников, треугольников, фигур позволяют изобразить однородные статистические показатели, не связанные друг с другом. Эти диаграммы используются для графического изображения статистических величин, характеризующих статику явления в разных совокупностях. Они также строятся в системе прямоугольных координат с соблюдением масштабности. Например, гистограммы применяются для графического изображения уровней смертности в разных возрастных группах населения; для демонстрации показателей больничной летальности в различных стационарах города; для изображения распространенности туберкулеза в различных социально-бытовых группах населения и т.д.
д) секторные диаграммы - используются для демонстрации структуры изучаемого явления, изображения части явления в целом. Они представляют собой круг, принимаемый за целое (100%), в котором отдельные секторы соответствуют частям изображаемого явления. Этот вид диаграмм применяется для графического изображения экстенсивных показателей. В секторных диаграммах секторы, изображающие отдельные части изучаемого явления, располагаются в порядке возрастания или убывания по движению часовой стрелки и имеют разный цвет или штриховку.
е) внутристолбиковые диаграммы также могут применяться для изображения структуры явления. При этом высота столбика принимается за 100%, весь столбик делится на составные части, которые соответствуют долям явления в процентах
ж) картограммы - это графические изображения, нанесенные на схемы географической карты, на которой различным цветом или штриховкой изображены степени распространенности явления по территории
з) картодиаграммы - такие графические изображения, при построении которых на карту или схему карты изучаемой территории проставляются диаграммы (столбиковые, фигурные, линейные)
86. Динамические ряды, их виды, методы выравнивания. Показатели.
При изучении динамики какого-либо явления прибегают к построению динамического ряда.
Динамический ряд - это ряд однородных статистических величин, показывающих изменение какого-либо явления во времени и расположенных в хронологическом порядке через определенные промежутки времени. Числа, составляющие динамический ряд, называются уровнями.
Уровень ряда- размер (величина) того или иного явления, достигнутый в определенный период или к определенному моменту времени. Уровни ряда могут быть представлены абсолютными, относительными или средними величинами.
Динамические ряды делятся на
а) простые (состоящие из абсолютных величин) - могут быть:
1) моментными- состоит из величин, характеризующих явление на какой-то определенный момент (статистические сведения, обычно регистрируемые на начало или конец месяца, квартала, года)
2) интервальными - состоит из чисел, характеризующих явление за определенный промежуток времени (интервал) - за неделю, месяц, квартал, год (данные о числе родившихся, умерших за год, число инфекционных заболеваний за месяц). Особенностью интервального ряда является то
, что его члены можно суммировать (при этом укрупняется интервал), или дробить.
б) сложные (состоящие из относительных или средних величин).
Динамические ряды могут подвергаться преобразованиям, целью которых является выявление особенностей изменения изучаемого процесса, а также достижение наглядности.
Показатели динамического ряда:
а) уровни ряда - величины членов ряда. Величина первого члена ряда носит название начального (исходного) уровня, величина последнего члена ряда - конечного уровня, средняя величина из всех членов ряда называется средним уровнем.
б) абсолютный прирост (убыль) - величина разности между последующим и предыдущим уровнями; прирост выражается числами с положительным знаком, убыль - с отрицательным знаком. Значение прироста или убыли отражают изменения уровней динамического ряда за определенный промежуток времени.
в) темп роста (снижения) - показывает отношение каждого последующего уровня к предыдущему уровню и обычно выражается в процентах.
г) темп прироста (убыли) - отношение абсолютного прироста или убыли каждого последующего члена ряда к уровню предыдущего, выраженное в процентах. Темп прироста может быть вычислен также по формуле: Темп роста - 100%
Абсолютное значение одного процента прироста (убыли) - получается от деления абсолютной величины прироста или убыли на показатель темпа прироста или убыли за тот же период.
Для более наглядного выражения нарастания или убывания ряда можно преобразовать его путем вычисления показателей наглядности, показывающих отношение каждого члена ряда к одному из них, принятому за сто процентов.
Иногда динамика изучаемого явления представлена не в виде непрерывно меняющегося уровня, а отдельными скачкообразными изменениями. В этом случае для выявления основной тенденции в развитии изучаемого явления прибегают к выравниванию динамического ряда. При этом могут быть использованы следующие приемы:
а) укрупнение интервала - суммирование данных за ряд смежных периодов. В результате получаются итоги за более продолжительные промежутки времени. Этим сглаживаются случайные колебания и более четко определяется характер динамики явления.
б) вычисление групповой средней